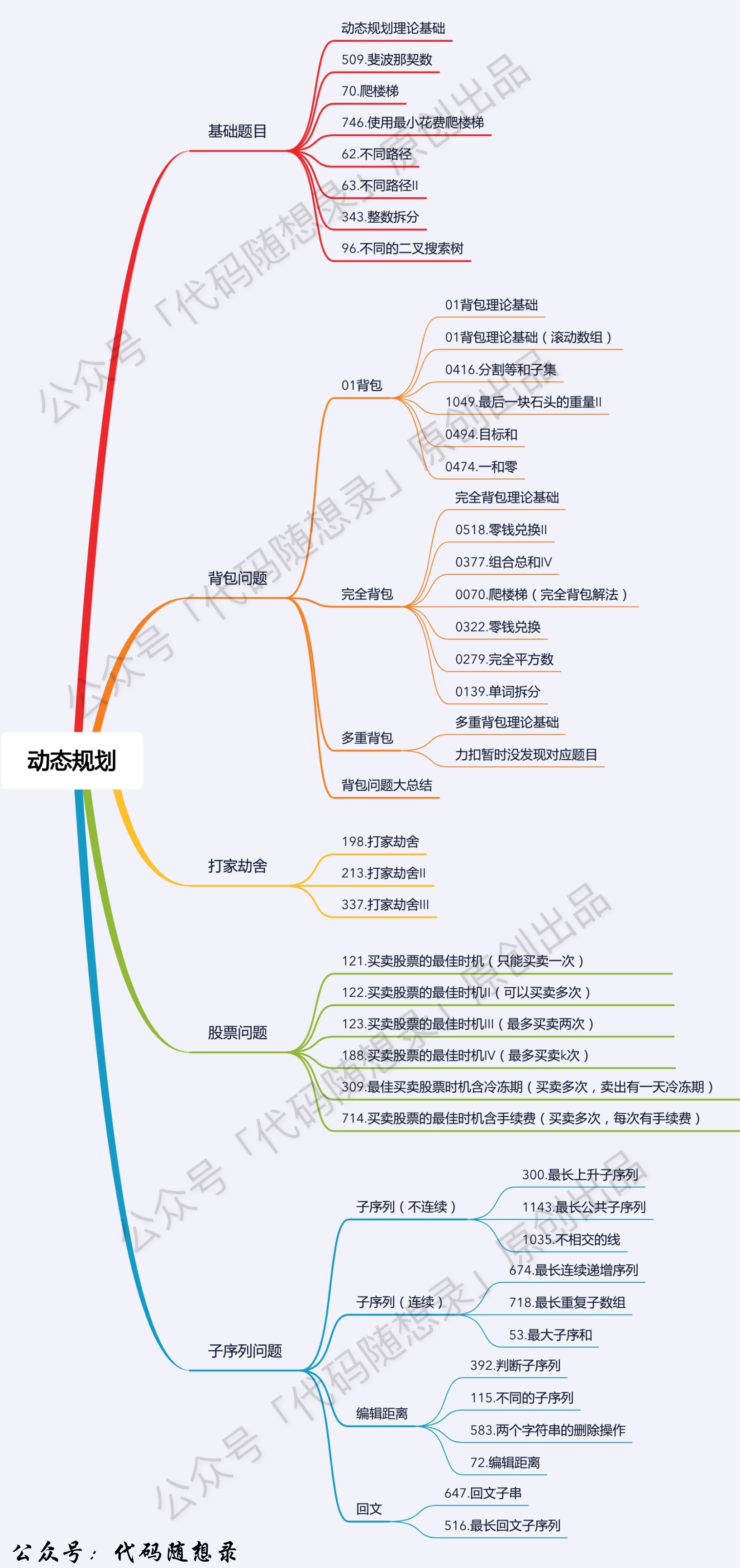
Dynamic Programming Fundamentals

Dynamic Programming Problem Outline

What is Dynamic Programming

Dynamic Programming, abbreviated as DP, is most effective for problems with many overlapping subproblems.

Thus, in dynamic programming, each state is derived from the previous state. This distinguishes it from greedy algorithms, where there is no state derivation and only the local optimum is chosen.

In Things You Should Know About Greedy Algorithms! (opens new window), I provided an example of a knapsack problem.

For example, you have N items and a knapsack with a maximum capacity of W. The weight of the i-th item is weight[i], and its value is value[i]. Each item can only be used once. The goal is to maximize the total value of the items in the knapsack.

In dynamic programming, dp[j] is derived from dp[j-weight[i]], and then max(dp[j], dp[j - weight[i]] + value[i]) is taken.

However, in a greedy algorithm, you simply pick the largest or smallest item each time, which is unrelated to the previous state.

This is why greedy algorithms can't solve dynamic programming problems.

You don't need to be too fixated on the theoretical differences between dynamic programming and greedy algorithms. Solving problems will naturally illustrate the distinction.

Many articles explaining dynamic programming discuss optimal substructures and overlapping subproblems. These are textbook definitions, often complex and not very practical.

Knowing that dynamic programming is based on deriving from a prior state and that greedy algorithms choose the local optimum is sufficient for problem-solving.

The knapsack problem mentioned above will be thoroughly explained later.

Steps for Solving Dynamic Programming Problems

When working on dynamic programming problems, many mistakenly believe that memorizing the state transition formula and modifying it slightly suffices. Even if the problem is AC, they may not understand what dp[i] represents.

This leads to a vague understanding and an ongoing cycle of referring to solutions and modifying templates without truly grasping the problem.

State transition formulas (recurrence relations) are crucial, but dynamic programming is more than just recurrence relations.

I will break down dynamic programming problems into five steps. Mastering these will mean truly understanding dynamic programming!

1. Define the dp array (dp table) and the meaning of indices
2. Determine the recurrence relation
3. Initialize the dp array
4. Define the order of iteration
5. Use examples to derive the dp array

Some may wonder why the recurrence relation is determined before considering initialization.

This is because, in some cases, how the dp array is initialized is influenced by the recurrence relation!

All my subsequent explanations will revolve around these five points.

Those who've tackled dynamic programming problems know the importance of recurrence relations. Finding it is akin to solving the problem.

However, determining the recurrence relation is just one part of the solution!

Some grasp the recurrence relation but struggle with initializing the dp array or determining the correct iteration order, leading to memorized formulas that can't be correctly implemented.

In later discussions, you'll recognize the significance of these five steps.

How to Debug Dynamic Programming Problems

For many, the approach to dynamic programming problems is:

1. Review a solution and feel as if they understand it.
2. Use the solution as a template.
3. If it works, great. If it doesn't, they're stuck, unsure of how to proceed.

If an issue arises, noting down each step of the dp array will help verify if it follows the intended logic.

Some approach dp learning as a black box, unaware of the dp array's meaning, why it's initialized a certain way, memorizing recurrence relations, and defaulting to habitual iteration orders. They write code in a burst and, if successful, assume it's correct. If not, they're clueless about where adjustments are needed.

This is an ineffective habit!

Before coding dynamic programming solutions, simulate the state transitions on the dp array to ensure it achieves the intended result.

Then code. If errors persist, print the dp array to pinpoint any discrepancies with your intended logic.

If the printed output matches your expectations but fails, the issue is likely a misalignment with the recurrence relation, initialization, or iteration order.

If it differs, the problem is likely in the implementation details.

This represents a thorough thought process, contrasted with aimless troubleshooting that sometimes inexplicably succeeds or fails.

This is why I emphasize the importance of deriving the dp array in the dynamic programming five-step framework.

For example, in the "Code Thinking" problem-solving squad WeChat group, when solutions fail, members post their code asking: My code matches the solution, why won't it pass?

Before posing such questions, consider these three points:

• Did I derive the recurrence relation using examples for this problem?
• Did I log the dp array?
• Does the dp array output match my expectations?

If you've reflected on these three questions, the problem is usually resolved, or you have clarity on what's unclear, such as the recurrence relation, coding implementation, or array iteration order.

Then, if you still need to ask questions, it will be more targeted, making it easier for others to assist.

This isn't to discourage questions but to encourage thoughtful and precise queries!

In the workplace, particularly in major companies, asking questions is a professional skill. Yes, asking questions must demonstrate professionalism!

If you pose unprofessional questions to colleagues, they may be reluctant to help, and leadership might perceive you as lacking critical thinking skills, which hinders career advancement.

Practicing professional inquiry when tackling problems hones valuable habits.

Summary

This article is an overview of dynamic programming, detailing what it is, problem-solving steps, and debugging methods.

Dynamic programming is a vast area. Today's content forms a foundational basis utilized throughout the dynamic programming series.

In subsequent discussions, we will delve into specific problems and their theoretical foundations, such as the 0/1 Knapsack, a common application of dynamic programming. However, problems incorporating pure 0/1 Knapsack issues will be fleshed out as needed.

You'll notice that the theoretical foundations I discuss aren't textbook definitions adorned with formulae but practical knowledge for problem-solving. This content is invaluable, so pay attention!

We're embarking on a new journey today. Are you ready?