# 647. Palindromic Substrings
LeetCode Problem Link (opens new window)
Given a string, your task is to count how many palindromic substrings are in it.
Substrings with different start or end positions are counted as different substrings even if they consist of the same characters.
Example 1:
- Input: "abc"
- Output: 3
- Explanation: Three palindromic substrings are: "a", "b", "c"
Example 2:
- Input: "aaa"
- Output: 6
- Explanation: Six palindromic substrings are: "a", "a", "a", "aa", "aa", "aaa"
Constraints: The length of the input string will not exceed 1000.
# Approach
# Brute Force
A brute force solution would use two nested for loops to iterate through all possible substrings and then a third loop to check if the current substring is a palindrome. This results in a time complexity of O(n^3).
# Dynamic Programming
The five steps of dynamic programming:
- Define the dp array (dp table) and the meaning of the indices
For most sequence-related problems, you naturally define the dp array based on what you are asked to find. However, for this problem, if we define dp[i] as the number of palindromic substrings ending at index i, it becomes hard to find a relation between dp[i], dp[i-1], and dp[i+1].
Thus, we need to consider the properties of palindromic substrings. When determining if a string S is a palindrome, if you know that the substring s[1] to s[3] is a palindrome, you only need to check if s[0] is equal to s[4] for S to be a palindrome.
This naturally leads to a recursive relation, judging whether a substring (from index [i,j]) is a palindrome depends on whether the substring s[i + 1, j - 1] is a palindrome.
Given this, we need a two-dimensional dp array.
Define dp[i][j]: A boolean indicator showing whether the substring in the range [i,j] (both inclusive) is a palindromic substring. If true, it’s a palindrome; if false, it is not.
- Determine the recurrence relation
Analyzing different scenarios when s[i] is equal to s[j] leads us to three cases:
- Case 1: If indices
iandjare the same, it is a single character, e.g., "a", which is a palindrome. - Case 2: If indices
iandjdiffer by 1, e.g., "aa", it is also a palindrome. - Case 3: If
iandjdiffer by more than 1, e.g., "cabac", sinces[i]equalss[j], check if the substringb[i+1]tob[j-1](i.e., "aba") is a palindrome, which meansdp[i + 1][j - 1]should be true.
Based on this analysis, the recurrence relation is:
if (s[i] == s[j]) {
if (j - i <= 1) { // Case 1 and Case 2
result++;
dp[i][j] = true;
} else if (dp[i + 1][j - 1]) { // Case 3
result++;
dp[i][j] = true;
}
}
2
3
4
5
6
7
8
9
The result tracks the count of palindromic substrings.
Notice that since dp[i][j] is initialized to false, if s[i] does not equal s[j], it does not affect our initialization.
- Initialize the dp array
We cannot initialize dp[i][j] to true. It starts as false since initially, no substring is considered a palindrome.
- Determine the traversal order
The traversal order is crucial.
The recurrence relation depends on dp[i + 1][j - 1]. Hence, the matrix should be filled such that dp[i + 1][j - 1] values are calculated before dp[i][j]. This can be accomplished by traversing from bottom to top, left to right.
Some implementations iterate columns first, then rows, which satisfies the same dependency.
Here is the code:
for (int i = s.size() - 1; i >= 0; i--) { // Ensure the correct traversal order
for (int j = i; j < s.size(); j++) {
if (s[i] == s[j]) {
if (j - i <= 1) { // Case 1 and Case 2
result++;
dp[i][j] = true;
} else if (dp[i + 1][j - 1]) { // Case 3
result++;
dp[i][j] = true;
}
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
- Example to illustrate the dp array
For input "aaa", the dp[i][j] becomes:
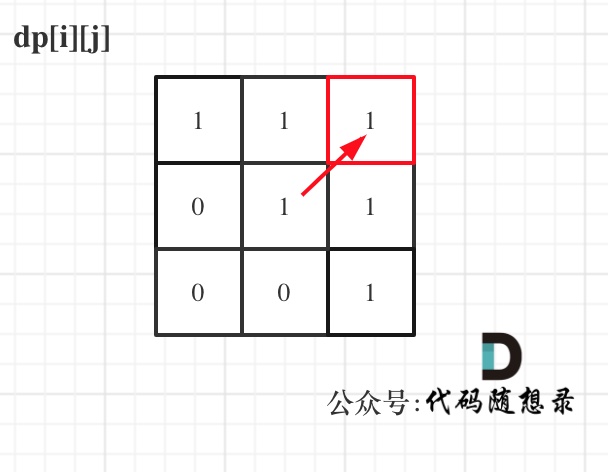
In the diagram, with 6 truths, we accurately account for six palindromic substrings.
Note that due to the definition of dp[i][j], j must be greater than or equal to i, ensuring only the upper half of the matrix is filled.
Complete analysis and solution below:
class Solution {
public:
int countSubstrings(string s) {
vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));
int result = 0;
for (int i = s.size() - 1; i >= 0; i--) { // Correct traversal order necessary
for (int j = i; j < s.size(); j++) {
if (s[i] == s[j]) {
if (j - i <= 1) { // Case 1 and Case 2
result++;
dp[i][j] = true;
} else if (dp[i + 1][j - 1]) { // Case 3
result++;
dp[i][j] = true;
}
}
}
}
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
The code is simplified for clarity:
class Solution {
public:
int countSubstrings(string s) {
vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));
int result = 0;
for (int i = s.size() - 1; i >= 0; i--) {
for (int j = i; j < s.size(); j++) {
if (s[i] == s[j] && (j - i <= 1 || dp[i + 1][j - 1])) {
result++;
dp[i][j] = true;
}
}
}
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
- Time Complexity: O(n^2)
- Space Complexity: O(n^2)
# Two-Pointer Approach
Since dynamic programming consumes more space, let's explore the two-pointer approach.
The approach basically focuses on expanding around the center and checking symmetry. Two center types must be considered:
- A single character center.
- A pair of characters as a center.
Some may argue there could be centers with three characters, but they can be derived by adding characters on sides of a single character. Similarly, a center with four characters can be derived via a double-character center.
Thus, handling these two cases separately is clearer:
class Solution {
public:
int countSubstrings(string s) {
int result = 0;
for (int i = 0; i < s.size(); i++) {
result += extend(s, i, i, s.size()); // Centered at single character
result += extend(s, i, i + 1, s.size()); // Centered between two characters
}
return result;
}
int extend(const string& s, int i, int j, int n) {
int res = 0;
while (i >= 0 && j < n && s[i] == s[j]) {
i--;
j++;
res++;
}
return res;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
- Time Complexity: O(n^2)
- Space Complexity: O(1)
# Other Language Versions
# Java:
Dynamic Programming:
class Solution {
public int countSubstrings(String s) {
char[] chars = s.toCharArray();
int len = chars.length;
boolean[][] dp = new boolean[len][len];
int result = 0;
for (int i = len - 1; i >= 0; i--) {
for (int j = i; j < len; j++) {
if (chars[i] == chars[j]) {
if (j - i <= 1) { // Case 1 and Case 2
result++;
dp[i][j] = true;
} else if (dp[i + 1][j - 1]) { // Case 3
result++;
dp[i][j] = true;
}
}
}
}
return result;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Dynamic Programming: Simplified Version
class Solution {
public int countSubstrings(String s) {
boolean[][] dp = new boolean[s.length()][s.length()];
int res = 0;
for (int i = s.length() - 1; i >= 0; i--) {
for (int j = i; j < s.length(); j++) {
if (s.charAt(i) == s.charAt(j) && (j - i <= 1 || dp[i + 1][j - 1])) {
res++;
dp[i][j] = true;
}
}
}
return res;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Center Expansion Method:
class Solution {
public int countSubstrings(String s) {
int len, ans = 0;
if (s == null || (len = s.length()) < 1) return 0;
// There are 2 * len - 1 centers total
for (int i = 0; i < 2 * len - 1; i++) {
// Traverse each center and expand while checking if it is a palindrome
int left = i / 2, right = left + i % 2;
while (left >= 0 && right < len && s.charAt(left) == s.charAt(right)) {
// If current is a palindrome, increase count
ans++;
left--;
right++;
}
}
return ans;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
LeetCode 5. Longest Palindromic Substring (a variation of LeetCode 647 can solve LeetCode 5 with some adjustments)
class Solution {
public String longestPalindrome(String s) {
int finalStart = 0;
int finalEnd = 0;
int finalLen = 0;
char[] chars = s.toCharArray();
int len = chars.length;
boolean[][] dp = new boolean[len][len];
for (int i = len - 1; i >= 0; i--) {
for (int j = i; j < len; j++) {
if (chars[i] == chars[j] && (j - i <= 1 || dp[i + 1][j - 1]))
dp[i][j] = true;
if (dp[i][j] && j - i + 1 > finalLen) {
finalLen = j - i + 1;
finalStart = i;
finalEnd = j;
}
}
}
return s.substring(finalStart, finalEnd + 1);
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# Python:
Dynamic Programming:
class Solution:
def countSubstrings(self, s: str) -> int:
dp = [[False] * len(s) for _ in range(len(s))]
result = 0
for i in range(len(s)-1, -1, -1): # Ensure correct traversal order
for j in range(i, len(s)):
if s[i] == s[j]:
if j - i <= 1: # Case 1 and Case 2
result += 1
dp[i][j] = True
elif dp[i+1][j-1]: # Case 3
result += 1
dp[i][j] = True
return result
2
3
4
5
6
7
8
9
10
11
12
13
14
Dynamic Programming: Simplified Version
class Solution:
def countSubstrings(self, s: str) -> int:
dp = [[False] * len(s) for _ in range(len(s))]
result = 0
for i in range(len(s)-1, -1, -1): # Ensure correct traversal order
for j in range(i, len(s)):
if s[i] == s[j] and (j - i <= 1 or dp[i+1][j-1]):
result += 1
dp[i][j] = True
return result
2
3
4
5
6
7
8
9
10
Two-Pointer Method:
class Solution:
def countSubstrings(self, s: str) -> int:
result = 0
for i in range(len(s)):
result += self.extend(s, i, i, len(s)) # Centered on single character
result += self.extend(s, i, i+1, len(s)) # Centered between two characters
return result
def extend(self, s, i, j, n):
res = 0
while i >= 0 and j < n and s[i] == s[j]:
i -= 1
j += 1
res += 1
return res
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# Go:
Dynamic Programming:
func countSubstrings(s string) int {
res:=0
dp:=make([][]bool,len(s))
for i:=0;i<len(s);i++{
dp[i]=make([]bool,len(s))
}
for i:=len(s)-1;i>=0;i--{
for j:=i;j<len(s);j++{
if s[i]==s[j]{
if j-i<=1{
res++
dp[i][j]=true
}else if dp[i+1][j-1]{
res++
dp[i][j]=true
}
}
}
}
return res
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Dynamic Programming: Simplified Version
func countSubstrings(s string) int {
res := 0
dp := make([][]bool, len(s))
for i := 0; i < len(s); i++ {
dp[i] = make([]bool, len(s))
}
for i := len(s) - 1; i >= 0; i-- {
for j := i; j < len(s); j++ {
if s[i] == s[j] && (j-i <= 1 || dp[i+1][j-1]) {
res++
dp[i][j] = true
}
}
}
return res
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Two-Pointer Method:
func countSubstrings(s string) int {
extend := func(i, j int) int {
res := 0
for i >= 0 && j < len(s) && s[i] == s[j] {
i --
j ++
res ++
}
return res
}
res := 0
for i := 0; i < len(s); i++ {
res += extend(i, i) // Centered at a single character
res += extend(i, i+1) // Centered between two characters
}
return res
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# JavaScript:
Dynamic Programming
const countSubstrings = (s) => {
const strLen = s.length;
let numOfPalindromicStr = 0;
let dp = Array.from(Array(strLen), () => Array(strLen).fill(false));
for(let j = 0; j < strLen; j++) {
for(let i = 0; i <= j; i++) {
if(s[i] === s[j]) {
if((j - i) < 2) {
dp[i][j] = true;
} else {
dp[i][j] = dp[i+1][j-1];
}
numOfPalindromicStr += dp[i][j] ? 1 : 0;
}
}
}
return numOfPalindromicStr;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Two-Pointer Method:
const countSubstrings = (s) => {
const strLen = s.length;
let numOfPalindromicStr = 0;
for(let i = 0; i < 2 * strLen - 1; i++) {
let left = Math.floor(i/2);
let right = left + i % 2;
while(left >= 0 && right < strLen && s[left] === s[right]){
numOfPalindromicStr++;
left--;
right++;
}
}
return numOfPalindromicStr;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# TypeScript:
Dynamic Programming:
function countSubstrings(s: string): number {
/**
dp[i][j]: [i,j] range's substring is a palindrome (both inclusive)
*/
const length: number = s.length;
const dp: boolean[][] = new Array(length).fill(0)
.map(_ => new Array(length).fill(false));
let resCount: number = 0;
// Bottom-up, left-to-right traversal
for (let i = length - 1; i >= 0; i--) {
for (let j = i; j < length; j++) {
if (
s[i] === s[j] &&
(j - i <= 1 || dp[i + 1][j - 1] === true)
) {
dp[i][j] = true;
resCount++;
}
}
}
return resCount;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Two-Pointer Method:
function countSubstrings(s: string): number {
const length: number = s.length;
let resCount: number = 0;
for (let i = 0; i < length; i++) {
resCount += expandRange(s, i, i);
resCount += expandRange(s, i, i + 1);
}
return resCount;
};
function expandRange(s: string, left: number, right: number): number {
let palindromeNum: number = 0;
while (
left >= 0 && right < s.length &&
s[left] === s[right]
) {
palindromeNum++;
left--;
right++;
}
return palindromeNum;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
Rust:
Dynamic Programming:
impl Solution {
pub fn count_substrings(s: String) -> i32 {
let mut dp = vec![vec![false; s.len()]; s.len()];
let mut res = 0;
for i in (0..s.len()).rev() {
for j in i..s.len() {
if s[i..=i] == s[j..=j] && (j - i <= 1 || dp[i + 1][j - 1]) {
dp[i][j] = true;
res += 1;
}
}
}
res
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Two-Pointer Method:
impl Solution {
pub fn count_substrings(s: String) -> i32 {
let mut res = 0;
for i in 0..s.len() {
res += Self::extend(&s, i, i, s.len());
res += Self::extend(&s, i, i + 1, s.len());
}
res
}
fn extend(s: &str, mut i: usize, mut j: usize, len: usize) -> i32 {
let mut res = 0;
while i < len && j < len && s[i..=i] == s[j..=j] {
res += 1;
i = i.wrapping_sub(1);
j += 1;
}
res
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
