Dynamic Programming: 01 Knapsack Theory Basics

This problem does not have a direct equivalent on LeetCode, but you can practice on KamaCoder Problem 46 (opens new window) which has the same meaning.

Thought Process

Let's officially start exploring knapsack problems!

For interviews, mastering 01 Knapsack and Complete Knapsack is sufficient; at most, you can also learn Multiple Knapsack.

If you can't distinguish these types of knapsacks, I've drawn a diagram here:

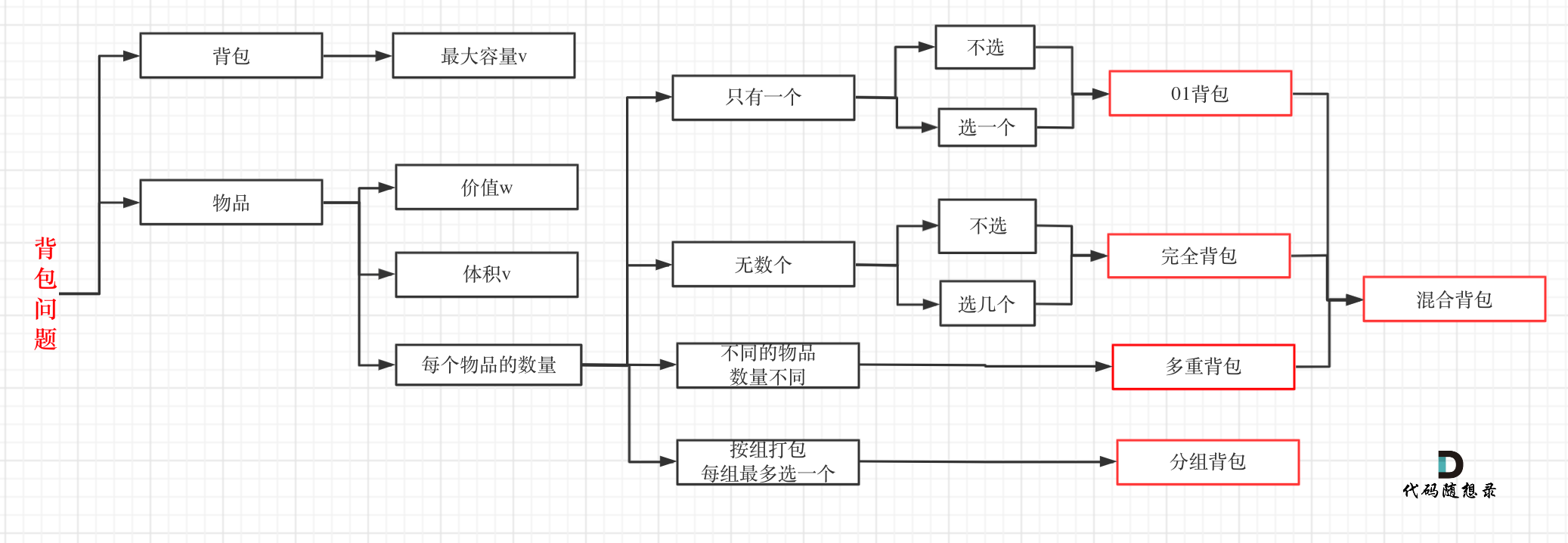
Other types of knapsacks are rarely asked in interviews and are usually for competitions; even LeetCode doesn't have questions on multiple knapsacks, so the problem set tells us that 01 Knapsack and Complete Knapsack are enough.

The Complete Knapsack is just a slight variation of 01 Knapsack, where the number of items is infinite.

Therefore, the 01 Knapsack theory is crucial to understand thoroughly!

LeetCode doesn't have pure 01 Knapsack problems; they are all applications of the 01 Knapsack problem, which means they need to be transformed into 01 Knapsack problems.

So I will first explain the 01 Knapsack principle through pure 01 Knapsack problems, and then focus on how to transform them into 01 Knapsack problems when discussing LeetCode problems later.

Some readers might be able to write knapsack solutions proficiently, but if you carefully read through this article, I believe you'll gain some unexpected insights!

01 Knapsack

There are n items and a knapsack with a maximum weight capacity of w. The weight of the i-th item is weight[i], and the value is value[i]. Each item can only be used once, determine which items to put in the knapsack to maximize the total value.

This is the standard knapsack problem, so many people naturally think of the knapsack without knowing how to solve it through brute force.

This actually doesn't think from the bottom up but instead habitually thinks of the knapsack. So what would be the brute force solution?

Each item basically has two states: take or not take, so we can use backtracking to search all situations, resulting in a time complexity of O(2^n), where n represents the number of items.

So the brute force solution is exponential, which necessitates an optimized solution using dynamic programming!

In the following explanation, I'll give an example:

The maximum weight capacity of the knapsack is 4.

Items are:

	Weight	Value
Item 0	1	15
Item 1	3	20
Item 2	4	30

The question is, what is the maximum value the knapsack can hold?

The numbers in the following explanation and diagram are based on this example.

(For convenience, the following descriptions consistently use a knapsack with capacity XX, storing a weight of XX item, and the item's value is XX)

2D dp Array 01 Knapsack

Let's analyze it with the five steps of dynamic programming.

1. Define the dp array and its index meanings

We need to use a 2D array, why?

Because there are two dimensions that need to be represented separately: items and knapsack capacity

As shown in the diagram, the 2D array is dp[i][j].

What do i, j, and dp[i][j] respectively indicate then?

i represents the item, and j represents the knapsack capacity.

(If you prefer using j to represent the item and i to represent the knapsack capacity, it's okay too; it's just personal preference.)

Let's try filling out the above 2D table.

Dynamic programming is about recursively solving sub-problems to derive the overall optimal solution.

Let's first consider the situation of putting item 0 in the knapsack:

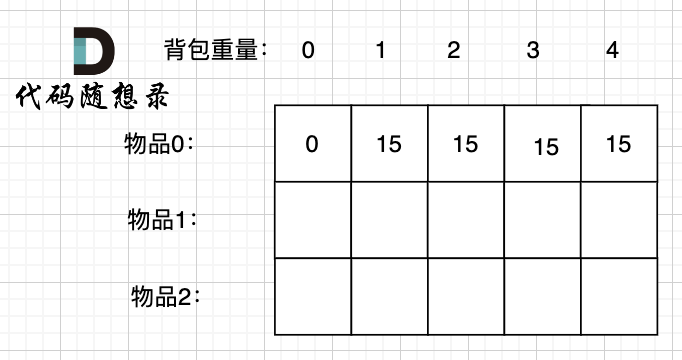
With a knapsack capacity of 0, item 0 cannot be stored; the total value in the knapsack is 0.

With a knapsack capacity of 1, item 0 can be stored; the total value is 15.

Just as well when the knapsack capacity is 2, item 0 can still be stored (note each 01 knapsack item is unique), and the total value is 15.

And so on.

Now let's consider item 1 being placed in the knapsack:

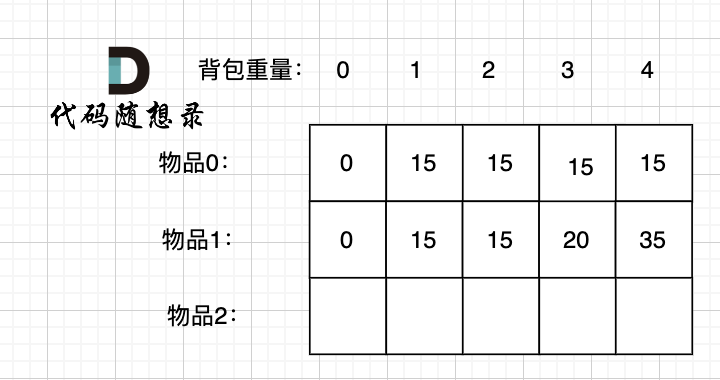
A knapsack capacity of 0 cannot store item 0 or item 1; the total value is 0.

With a knapsack capacity of 1, only item 0 can be stored, giving a value in the knapsack of 15.

With a knapsack capacity of 2, only item 0 can be stored, which gives a value of 15.

With a knapsack capacity of 3, either item 1 or item 0 can now be chosen, with item 1 being more valuable, making the knapsack's value 20.

With a knapsack capacity of 4, both item 0 and item 1 can be stored, making the knapsack's value 35.

The above example is relatively easy to understand. I'm mainly trying to help clarify the meaning of the dp array.

From the above image, what does dp[1][4] indicate?

Taking any of item 0 and item 1, and placing them in a knapsack with a capacity of 4, achieving a maximum value of dp[1][4].

From this example, let's further clarify the meaning of the dp array.

That is, dp[i][j] indicates the maximum value that can be obtained from taking any of the items with indices [0-i] and placing them in a knapsack with capacity j.

Always remember this meaning of the dp array, and the following steps revolve around the definition of this dp array. If you feel confused, come back and recall what i represents and what j represents.

2. Establish the Recursive Formula

We'll provide the basic information:

	Weight	Value
Item 0	1	15
Item 1	3	20
Item 2	4	30

For the recursive formula, we need to clarify which directions can derive dp[i][j].

Here, we'll take the state of dp[1][4] as an example:

To derive dp[1][4], there are two possibilities:

1. Place item 1
2. Or don't place item 1

If item 1 is not placed, then the knapsack's value should be dp[0][4], which is the situation where the knapsack has a capacity of 4 and only item 0 is placed.

The derivation direction is as shown:

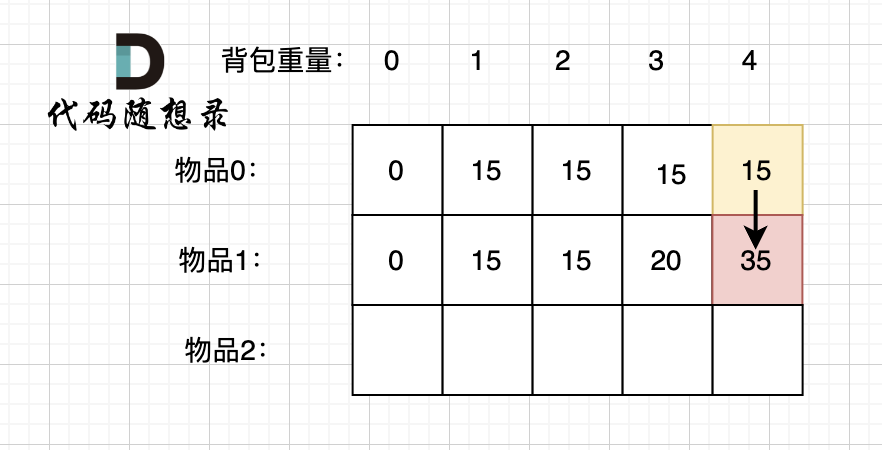
If item 1 is placed, then the knapsack must reserve space for item 1. Currently, the capacity is 4, and the capacity (weight) of item 1 is 3, so the remaining space in the knapsack is 1.

With a capacity of 1, the maximum value for only considering placing item 0 is dp[0][1], which we've already calculated before.

So, considering placing item 1 = dp[0][1] + the value of item 1, as shown in the derivation direction:

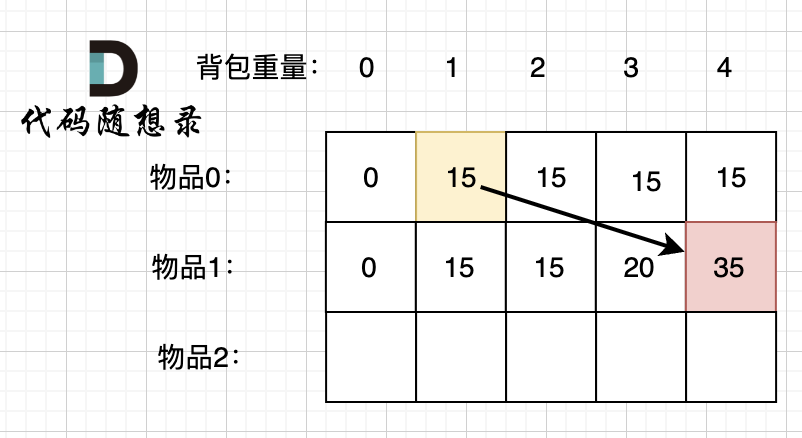
Taking the maximum value from both possibilities (placing item 1 and not placing item 1) since we aim to achieve the maximum value, gives us:

dp[1][4] = max(dp[0][4], dp[0][1] + the value of item 1)

This process is abstract as follows:

• Not placing item i: A knapsack with capacity j without placing item i has a maximum value of dp[i - 1][j].

• Placing item i: After making space for item i, the knapsack's capacity is j - weight[i]. dp[i - 1][j - weight[i]] is the maximum value for the knapsack with capacity j - weight[i] without placing item i, then dp[i - 1][j - weight[i]] + value[i] (the value of item i) is the maximum value the knapsack gets by placing item i.

The recursive formula is: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

3. dp Array Initialization

About the initialization, be sure to align it with the dp array definition, otherwise, as recursive formulas progress, it will become increasingly disordered.

Starting from the definition of dp[i][j], if the knapsack's capacity j is 0, i.e., dp[i][0], regardless of which items are selected, the knapsack's total value is guaranteed to be 0. As shown:

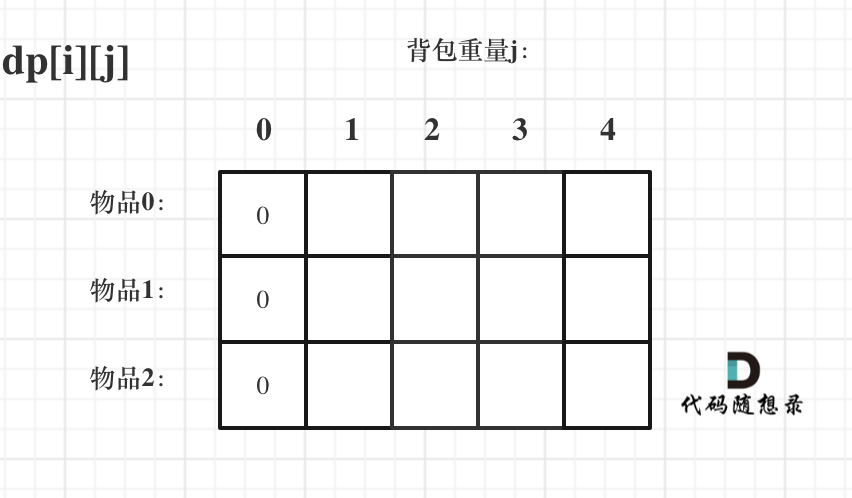
Let's consider other situations.

From the state transfer formula dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);, we see that i is derived from i-1, so i = 0 inevitably needs initialization.

dp[0][j], that is, when i is 0, storing item 0, varies with knapsack capacities and the maximum obtainable value.

Obviously, when j < weight[0], dp[0][j] should be 0, because the knapsack capacity is less than the item 0's weight.

When j >= weight[0], dp[0][j] should be value[0], because the knapsack capacity is sufficiently enough for item 0.

Code initialization follows:

for (int i = 1; i < weight.size(); i++) {  // Of course, this step can be omitted if the `dp` array was pre-initialized with 0, but many might not have considered this.
    dp[i][0] = 0;
}
// Iterate in order
for (int j = weight[0]; j <= bagweight; j++) {
    dp[0][j] = value[0];
}

At this point, the dp array's initialization is as follows:

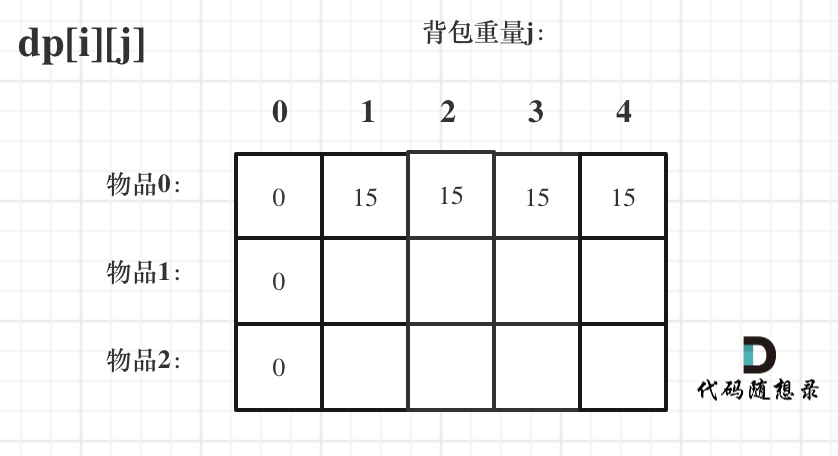
With both dp[0][j] and dp[i][0] initialized. But how should the initial values of other indices be?

Actually, from the recursive formula: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);, we can infer that dp[i][j] is derived from the upper-left numbers, so it can be initialized to any number since it will be overridden.

Initialize to -1, -2, 100, all okay!

But generally, initializing the dp array uniformly to 0 upfront is more convenient.

As shown:

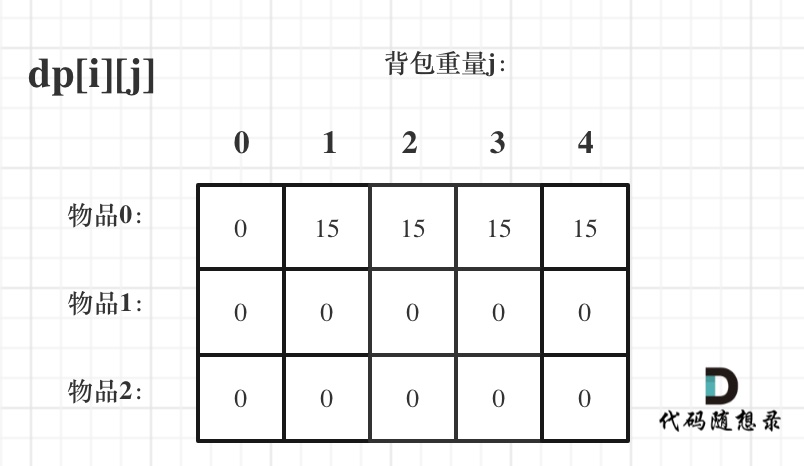
Finally, the initialization code is as follows:

// Initialize dp
vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));
for (int j = weight[0]; j <= bagweight; j++) {
    dp[0][j] = value[0];
}

It's taken such effort to explain initialization clearly, and I believe many people typically initialize the dp array based on intuition, but intuition can be unreliable.

4. Determine the Traversal Order

From the diagram below, it can be seen that there are two traversal dimensions: items and knapsack weight.

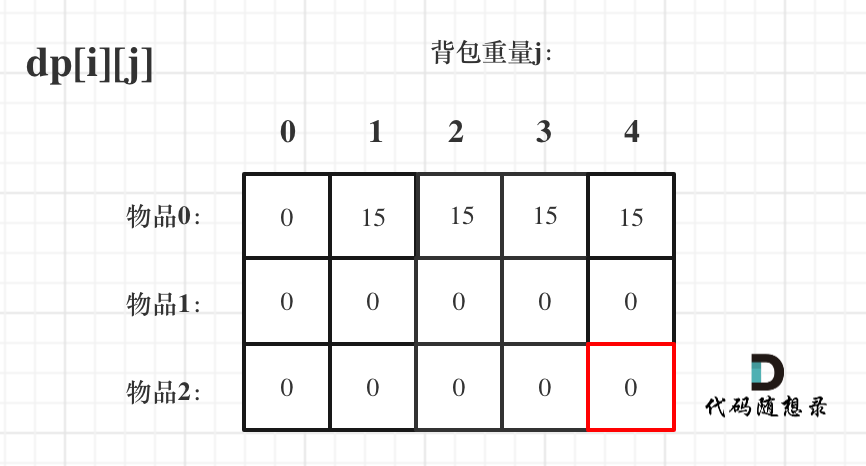
Which order to traverse first, items or knapsack weight?

Actually both are possible! But it's easier to understand by traversing items first.

I'll first provide the code for traversing items first and then knapsack weight.

// The size of the weight array is the number of items
for(int i = 1; i < weight.size(); i++) { // Traverse items
    for(int j = 0; j <= bagweight; j++) { // Traverse knapsack capacity
        if (j < weight[i]) dp[i][j] = dp[i - 1][j];
        else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
    }
}

It's also possible to traverse the knapsack first and then items! (Note I'm using a 2D dp array here)

For example, like this:

// The size of the weight array is the number of items
for(int j = 0; j <= bagweight; j++) { // Traverse knapsack capacity
    for(int i = 1; i < weight.size(); i++) { // Traverse items
        if (j < weight[i]) dp[i][j] = dp[i - 1][j];
        else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
    }
}

Why is this also possible?

To understand the essence of recursion and the direction of recursion.

dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); We can see from the recursive formula that dp[i][j] relies on dp[i-1][j] and dp[i - 1][j - weight[i]].

dp[i-1][j] and dp[i - 1][j - weight[i]] are all located diagonally at the upper-left of dp[i][j], thus first traversing items before knapsacks looks like this:

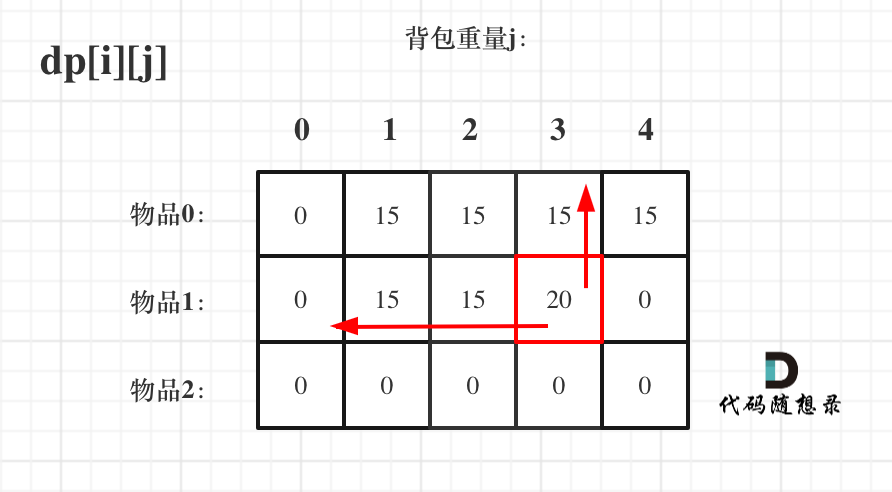
Now consider traversing the knapsack first and then items, as shown:

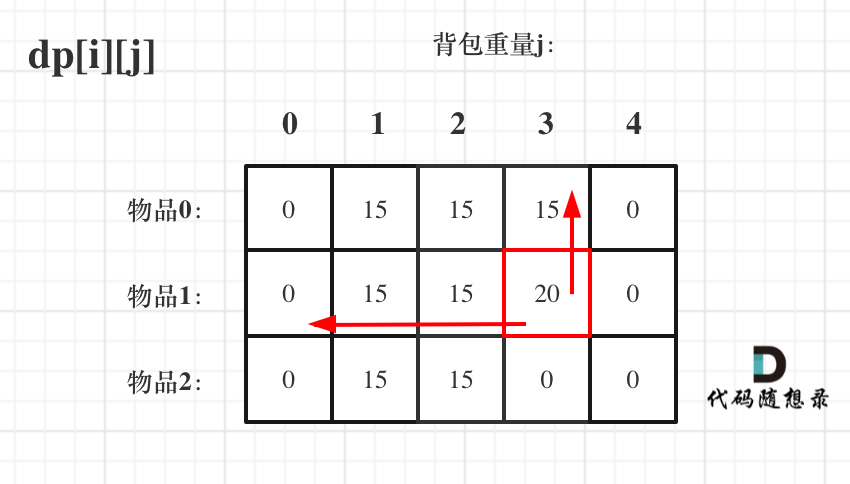
You can see that although the two for loop traversal orders differ, the data dp[i][j] needs is always from the upper-left, which doesn’t impact the derivation of dp[i][j]!

Yet, it's easier to understand to traverse items first and then knapsack capacity.

In knapsack problems, the order of for loops is very important and typically harder to comprehend compared to the recursive formula.

5. Example Walkthrough of the dp Array

Let's take a look at the value of the dp array values, as shown:

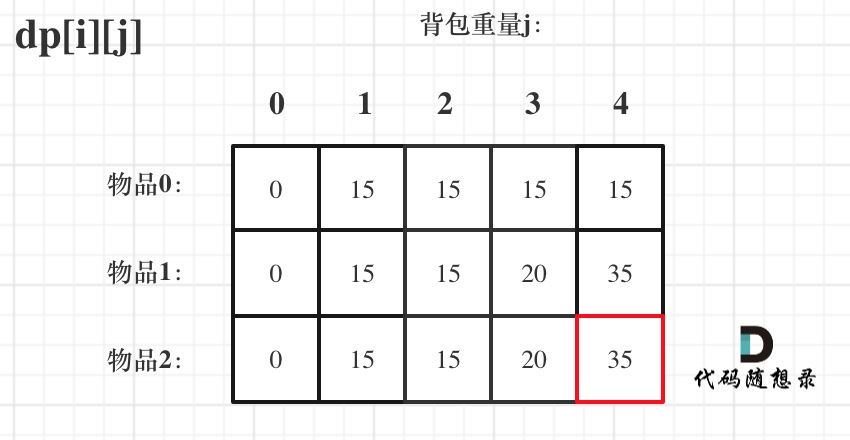
The final result is dp[2][4].

At this point, I suggest you work through on paper to check if every number matches as shown in the dp array.

When tackling dynamic programming problems, the best way is to manually walk through an example on paper and derive the corresponding dp array's values, and then write the code!

Plenty of learners encounter dynamic programming problems, make various attempts and haphazard changes, and still can't get it right, or they randomly get it correct with confusion.

This mainly comes down to not manually deriving how dp arrays change. If derived thoroughly, even if the code is incorrect, simply printing the dp array and comparing helps swiftly identify the problem.

For this problem, LeetCode doesn't have an equivalent, but you could go to KamaCoder Problem 46 (opens new window) with the same meaning; the code is as follows:

#include <bits/stdc++.h>
using namespace std;

int main() {
    int n, bagweight;// bagweight stands for the knapsack space

    cin >> n >> bagweight;

    vector<int> weight(n, 0); // Stores the space each item occupies
    vector<int> value(n, 0);  // Stores the value of each item

    for(int i = 0; i < n; ++i) {
        cin >> weight[i];
    }
    for(int j = 0; j < n; ++j) {
        cin >> value[j];
    }
    // dp array, dp[i][j] represents for knapsack space j, out of [0, i] items any can be taken to maximize the value
    vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));

    // Initialization, since it requires the value of dp[i - 1]
    // j < weight[0] has been initialized to 0 above
    // The value for j >= weight[0] is initialized to value[0]
    for (int j = weight[0]; j <= bagweight; j++) {
        dp[0][j] = value[0];
    }

    for(int i = 1; i < weight.size(); i++) { // Iterate over research items
        for(int j = 0; j <= bagweight; j++) { // Iterate over knapsack capacity
            if (j < weight[i]) dp[i][j] = dp[i - 1][j]; // If this item cannot be accommodated, then inherit the value of dp[i - 1][j]
            else {
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
            }
        }
    }
    cout << dp[n - 1][bagweight] << endl;

    return 0;
}

Summary

The knapsack problem is a classic type in dynamic programming, and should be savored thoughtfully.

Some of you may not have noticed the importance of initialization and traversal order; you'll feel it once we tackle knapsack problems in interview scenarios on LeetCode.

The next article will still cover theory basics, where we will discuss the 01 Knapsack implemented with a 1D dp array (rolling array), and analyze the differences with 2D arrays, as well as the variations in their initialization and traversal orders.

Other Language Versions

Java

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int bagweight = scanner.nextInt();

        int[] weight = new int[n];
        int[] value = new int[n];

        for (int i = 0; i < n; ++i) {
            weight[i] = scanner.nextInt();
        }
        for (int j = 0; j < n; ++j) {
            value[j] = scanner.nextInt();
        }

        int[][] dp = new int[n][bagweight + 1];

        for (int j = weight[0]; j <= bagweight; j++) {
            dp[0][j] = value[0];
        }

        for (int i = 1; i < n; i++) {
            for (int j = 0; j <= bagweight; j++) {
                if (j < weight[i]) {
                    dp[i][j] = dp[i - 1][j];
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
                }
            }
        }

        System.out.println(dp[n - 1][bagweight]);
    }
}

Python

n, bagweight = map(int, input().split())

weight = list(map(int, input().split()))
value = list(map(int, input().split()))

dp = [[0] * (bagweight + 1) for _ in range(n)]

for j in range(weight[0], bagweight + 1):
    dp[0][j] = value[0]

for i in range(1, n):
    for j in range(bagweight + 1):
        if j < weight[i]:
            dp[i][j] = dp[i - 1][j]
        else:
            dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])

print(dp[n - 1][bagweight])

Go

package main

import (
    "fmt"
)

func main() {
    var n, bagweight int // bagweight stands for the knapsack space
    fmt.Scan(&n, &bagweight)

    weight := make([]int, n) // Stores the space each item occupies
    value := make([]int, n)  // Stores the value of each item

    for i := 0; i < n; i++ {
        fmt.Scan(&weight[i])
    }
    for j := 0; j < n; j++ {
        fmt.Scan(&value[j])
    }
    // dp array, dp[i][j] represents for knapsack space j, out of [0, i] items any can be taken to maximize the value
    dp := make([][]int, n)
    for i := range dp {
        dp[i] = make([]int, bagweight + 1)
    }

    // Initialization, since it requires the value of dp[i - 1]
    // j < weight[0] has been initialized to 0 above
    // The value for j >= weight[0] is initialized to value[0]
    for j := weight[0]; j <= bagweight; j++ {
        dp[0][j] = value[0]
    }

    for i := 1; i < n; i++ { // Iterate over research items
        for j := 0; j <= bagweight; j++ { // Iterate over knapsack capacity
            if j < weight[i] {
                dp[i][j] = dp[i-1][j] // If this item cannot be accommodated, then inherit the value of dp[i - 1][j]
            } else {
                dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]]+value[i])
            }
        }
    }

    fmt.Println(dp[n-1][bagweight])
}

func max(x, y int) int {
    if x > y {
        return x
    }
    return y
}

JavaScript

const readline = require('readline').createInterface({
    input: process.stdin,
    output: process.stdout
});

let input = [];

readline.on('line', (line) => {
    input.push(line);
});

readline.on('close', () => {
    let [n, bagweight] = input[0].split(' ').map(Number);
    let weight = input[1].split(' ').map(Number);
    let value = input[2].split(' ').map(Number);

    let dp = Array.from({ length: n }, () => Array(bagweight + 1).fill(0));

    for (let j = weight[0]; j <= bagweight; j++) {
        dp[0][j] = value[0];
    }

    for (let i = 1; i < n; i++) {
        for (let j = 0; j <= bagweight; j++) {
            if (j < weight[i]) {
                dp[i][j] = dp[i - 1][j];
            } else {
                dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
            }
        }
    }

    console.log(dp[n - 1][bagweight]);
});

C

#include <stdio.h>
#include <stdlib.h>

int max(int a, int b) {
    return a > b ? a : b;
}

int main() {
    int n, bagweight;
    scanf("%d %d", &n, &bagweight);

    int *weight = (int *)malloc(n * sizeof(int));
    int *value = (int *)malloc(n * sizeof(int));

    for (int i = 0; i < n; ++i) {
        scanf("%d", &weight[i]);
    }
    for (int j = 0; j < n; ++j) {
        scanf("%d", &value[j]);
    }

    int **dp = (int **)malloc(n * sizeof(int *));
    for (int i = 0; i < n; ++i) {
        dp[i] = (int *)malloc((bagweight + 1) * sizeof(int));
        for (int j = 0; j <= bagweight; ++j) {
            dp[i][j] = 0;
        }
    }

    for (int j = weight[0]; j <= bagweight; j++) {
        dp[0][j] = value[0];
    }

    for (int i = 1; i < n; i++) {
        for (int j = 0; j <= bagweight; j++) {
            if (j < weight[i]) {
                dp[i][j] = dp[i - 1][j];
            } else {
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
            }
        }
    }

    printf("%d\n", dp[n - 1][bagweight]);

    for (int i = 0; i < n; ++i) {
        free(dp[i]);
    }
    free(dp);
    free(weight);
    free(value);

    return 0;
}