# 63. Unique Paths II
LeetCode Problem Link (opens new window)
A robot is located at the top-left corner of an m x n grid (marked "Start" in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked "Finish" in the diagram below).
Now consider if some obstacles are added to the grids. How many unique paths would there be?

An obstacle and empty space are marked as 1 and 0 respectively in the grid.
Example 1:
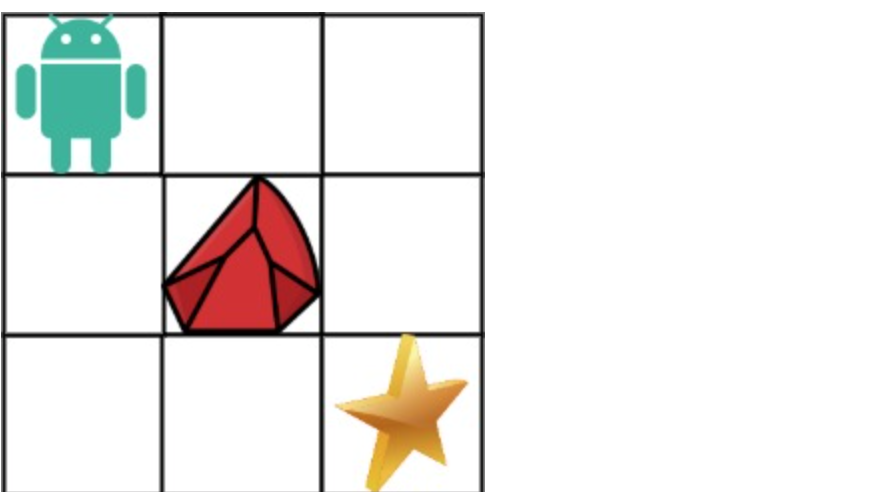
- Input:
obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]] - Output:
2Explanation: - There is an obstacle in the middle of the 3x3 grid.
- There are two unique paths from top-left to bottom-right:
- Right -> Right -> Down -> Down
- Down -> Down -> Right -> Right
Example 2:

- Input:
obstacleGrid = [[0,1],[0,0]] - Output:
1
Constraints:
m == obstacleGrid.lengthn == obstacleGrid[i].length1 <= m, n <= 100obstacleGrid[i][j]is either0or1
# Approach
This problem adds obstacles which makes it slightly different from the problem 0062.Unique Paths (opens new window).
For beginners, it might be a bit confusing when obstacles are introduced. But it essentially means marking the respective positions in the dp table (or dp array) to remain at the initial value (0).
Dynamic Programming Approach:
Define the
dparray meaning:dp[i][j]: It represents the number of unique paths to reach position(i, j)from(0, 0).Transition formula:
The transition formula is similar to that in 0062. Unique Paths (opens new window):
[ dp[i][j] = dp[i - 1][j] + dp[i][j - 1] ] Be cautious when there is an obstacle at(i, j), in which casedp[i][j]should remain at the initial state (0).
if (obstacleGrid[i][j] == 0) { // only when there is no obstacle at (i, j), we update dp[i][j]
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
2
3
Initialize
dparray:In 0062. Unique Paths (opens new window), we initialized as follows:
vector<vector<int>> dp(m, vector<int>(n, 0)); // initial value 0
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;
2
3
Here, if there's an obstacle after point (i, 0), all positions including and after it in the first column should remain zero.
Similarly for row (0, j).
vector<vector<int>> dp(m, vector<int>(n, 0));
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;
2
3
Note the termination condition in the for loop. If obstacleGrid[i][0] == 1, stop assigning 1 to dp[i][0], similarly for dp[0][j].
Determine traversal order:
From the recursive formula
dp[i][j] = dp[i-1][j] + dp[i][j-1], it's clear we traverse from left to right, layer by layer, ensuringdp[i-1][j]anddp[i][j-1]are computed beforedp[i][j].
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (obstacleGrid[i][j] == 1) continue;
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
2
3
4
5
6
Example to derive the
dparray:Taking Example 1 for illustration:
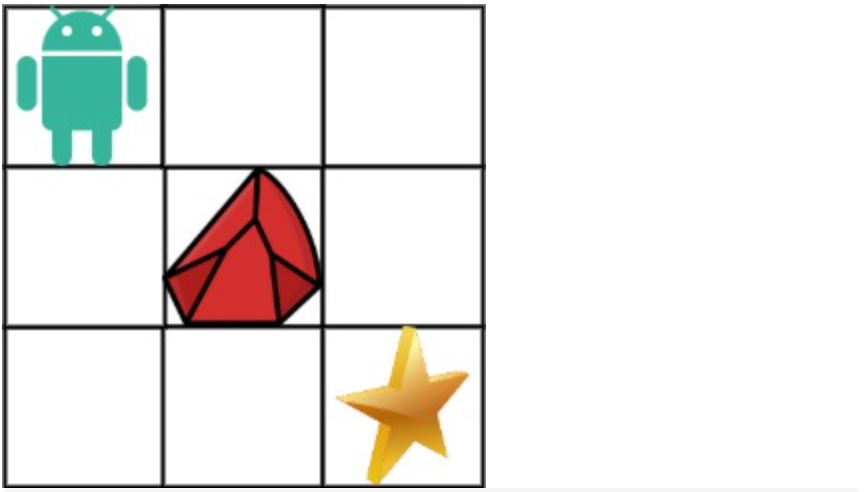
The corresponding dp table is as follows:
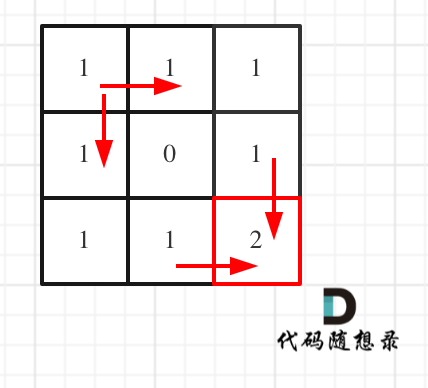
If unclear, it helps to understand the transition formula and manually derive it following the discussed traversal order!
Here's the complete C++ code:
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
int m = obstacleGrid.size();
int n = obstacleGrid[0].size();
if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1)
return 0;
vector<vector<int>> dp(m, vector<int>(n, 0));
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
if (obstacleGrid[i][j] == 1) continue;
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
- Time Complexity: O(n × m), where n, m are the dimensions of
obstacleGrid. - Space Complexity: O(n × m)
Now, an optimized space version:
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
if (obstacleGrid[0][0] == 1)
return 0;
vector<int> dp(obstacleGrid[0].size());
for (int j = 0; j < dp.size(); ++j)
if (obstacleGrid[0][j] == 1)
dp[j] = 0;
else if (j == 0)
dp[j] = 1;
else
dp[j] = dp[j-1];
for (int i = 1; i < obstacleGrid.size(); ++i)
for (int j = 0; j < dp.size(); ++j){
if (obstacleGrid[i][j] == 1)
dp[j] = 0;
else if (j != 0)
dp[j] = dp[j] + dp[j-1];
}
return dp.back();
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
- Time Complexity: O(n × m)
- Space Complexity: O(m)
# Summary
This problem is a variant of 0062. Unique Paths (opens new window) with the addition of obstacles, while the main logic remains similar.
Nonetheless, even having solved 0062. Unique Paths, one might find it tricky initially with the added complexity of obstacles.
Essentially, when encountering an obstacle, keep dp[i][j] at 0.
Mind the finer points, such as initialization, where cells past an obstacle remain zero.
# Java
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int m = obstacleGrid.length;
int n = obstacleGrid[0].length;
int[][] dp = new int[m][n];
if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) {
return 0;
}
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) {
dp[i][0] = 1;
}
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) {
dp[0][j] = 1;
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = (obstacleGrid[i][j] == 0) ? dp[i - 1][j] + dp[i][j - 1] : 0;
}
}
return dp[m - 1][n - 1];
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
Optimized space version:
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int m = obstacleGrid.length;
int n = obstacleGrid[0].length;
int[] dp = new int[n];
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) {
dp[j] = 1;
}
for (int i = 1; i < m; i++) {
for (int j = 0; j < n; j++) {
if (obstacleGrid[i][j] == 1) {
dp[j] = 0;
} else if (j != 0) {
dp[j] += dp[j - 1];
}
}
}
return dp[n - 1];
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# Python
Dynamic Programming (Version 1)
class Solution:
def uniquePathsWithObstacles(self, obstacleGrid):
m = len(obstacleGrid)
n = len(obstacleGrid[0])
if obstacleGrid[m - 1][n - 1] == 1 or obstacleGrid[0][0] == 1:
return 0
dp = [[0] * n for _ in range(m)]
for i in range(m):
if obstacleGrid[i][0] == 0:
dp[i][0] = 1
else:
break
for j in range(n):
if obstacleGrid[0][j] == 0:
dp[0][j] = 1
else:
break
for i in range(1, m):
for j in range(1, n):
if obstacleGrid[i][j] == 1:
continue
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
return dp[m - 1][n - 1]
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Dynamic Programming (Version 2)
class Solution:
def uniquePathsWithObstacles(self, obstacleGrid):
m = len(obstacleGrid)
n = len(obstacleGrid[0])
if obstacleGrid[m - 1][n - 1] == 1 or obstacleGrid[0][0] == 1:
return 0
dp = [[0] * n for _ in range(m)]
dp[0][0] = 1 if obstacleGrid[0][0] == 0 else 0
for i in range(1, m):
if obstacleGrid[i][0] == 0:
dp[i][0] = dp[i - 1][0]
for j in range(1, n):
if obstacleGrid[0][j] == 0:
dp[0][j] = dp[0][j - 1]
for i in range(1, m):
for j in range(1, n):
if obstacleGrid[i][j] == 1:
continue
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
return dp[m - 1][n - 1]
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
Dynamic Programming (Version 3)
class Solution:
def uniquePathsWithObstacles(self, obstacleGrid):
if obstacleGrid[0][0] == 1:
return 0
dp = [0] * len(obstacleGrid[0])
for j in range(len(dp)):
if obstacleGrid[0][j] == 1:
dp[j] = 0
elif j == 0:
dp[j] = 1
else:
dp[j] = dp[j - 1]
for i in range(1, len(obstacleGrid)):
for j in range(len(dp)):
if obstacleGrid[i][j] == 1:
dp[j] = 0
elif j != 0:
dp[j] = dp[j] + dp[j - 1]
return dp[-1]
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Dynamic Programming (Version 4)
class Solution:
def uniquePathsWithObstacles(self, obstacleGrid):
if obstacleGrid[0][0] == 1:
return 0
m, n = len(obstacleGrid), len(obstacleGrid[0])
dp = [0] * n
for j in range(n):
if obstacleGrid[0][j] == 1:
break
dp[j] = 1
for i in range(1, m):
if obstacleGrid[i][0] == 1:
dp[0] = 0
for j in range(1, n):
if obstacleGrid[i][j] == 1:
dp[j] = 0
else:
dp[j] += dp[j - 1]
return dp[-1]
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
Dynamic Programming (Version 5)
class Solution:
def uniquePathsWithObstacles(self, obstacleGrid):
if obstacleGrid[0][0] == 1:
return 0
m, n = len(obstacleGrid), len(obstacleGrid[0])
dp = [0] * n
for j in range(n):
if obstacleGrid[0][j] == 1:
break
dp[j] = 1
for i in range(1, m):
if obstacleGrid[i][0] == 1:
dp[0] = 0
for j in range(1, n):
if obstacleGrid[i][j] == 1:
dp[j] = 0
continue
dp[j] += dp[j - 1]
return dp[-1]
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# Go
func uniquePathsWithObstacles(obstacleGrid [][]int) int {
m, n := len(obstacleGrid), len(obstacleGrid[0])
if obstacleGrid[m-1][n-1] == 1 || obstacleGrid[0][0] == 1 {
return 0
}
dp := make([][]int, m)
for i := range dp {
dp[i] = make([]int, n)
}
for i := 0; i < m && obstacleGrid[i][0] == 0; i++ {
dp[i][0] = 1
}
for i := 0; i < n && obstacleGrid[0][i] == 0; i++ {
dp[0][i] = 1
}
for i := 1; i < m; i++ {
for j := 1; j < n; j++ {
if obstacleGrid[i][j] != 1 {
dp[i][j] = dp[i-1][j] + dp[i][j-1]
}
}
}
return dp[m-1][n-1]
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# JavaScript
var uniquePathsWithObstacles = function(obstacleGrid) {
const m = obstacleGrid.length
const n = obstacleGrid[0].length
const dp = Array(m).fill().map(item => Array(n).fill(0))
for (let i = 0; i < m && obstacleGrid[i][0] === 0; ++i) {
dp[i][0] = 1
}
for (let i = 0; i < n && obstacleGrid[0][i] === 0; ++i) {
dp[0][i] = 1
}
for (let i = 1; i < m; ++i) {
for (let j = 1; j < n; ++j) {
dp[i][j] = obstacleGrid[i][j] === 1 ? 0 : dp[i - 1][j] + dp[i][j - 1]
}
}
return dp[m - 1][n - 1]
};
// Optimized Version: use the original array as the dp array
var uniquePathsWithObstacles = function(obstacleGrid) {
const m = obstacleGrid.length;
const n = obstacleGrid[0].length;
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
if (obstacleGrid[i][j] === 0) {
if (i === 0) {
obstacleGrid[i][j] = obstacleGrid[i][j - 1] ?? 1;
} else if (j === 0) {
obstacleGrid[i][j] = obstacleGrid[i - 1]?.[j] ?? 1;
} else {
obstacleGrid[i][j] = obstacleGrid[i - 1][j] + obstacleGrid[i][j - 1];
}
} else {
obstacleGrid[i][j] = 0;
}
}
}
return obstacleGrid[m - 1][n - 1];
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
# TypeScript
function uniquePathsWithObstacles(obstacleGrid: number[][]): number {
const m: number = obstacleGrid.length;
const n: number = obstacleGrid[0].length;
const dp: number[][] = new Array(m).fill(0).map(_ => new Array(n).fill(0));
for (let i = 0; i < m && obstacleGrid[i][0] === 0; i++) {
dp[i][0] = 1;
}
for (let i = 0; i < n && obstacleGrid[0][i] === 0; i++) {
dp[0][i] = 1;
}
for (let i = 1; i < m; i++) {
for (let j = 1; j < n; j++) {
if (obstacleGrid[i][j] === 1) continue;
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Optimized to 1D array, traversing from end to start:
function uniquePathsWithObstacles(obstacleGrid: number[][]): number {
const m = obstacleGrid.length;
const n = obstacleGrid[0].length;
const dp: number[] = new Array(n).fill(0);
dp[n - 1] = 1;
for (let i = m - 1; i >= 0; i--) {
for (let j = n - 1; j >= 0; j--) {
if (obstacleGrid[i][j] === 1) dp[j] = 0;
else dp[j] = dp[j] + (dp[j + 1] || 0);
}
}
return dp[0];
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# Rust
impl Solution {
pub fn unique_paths_with_obstacles(obstacle_grid: Vec<Vec<i32>>) -> i32 {
let m: usize = obstacle_grid.len();
let n: usize = obstacle_grid[0].len();
if obstacle_grid[0][0] == 1 || obstacle_grid[m-1][n-1] == 1 {
return 0;
}
let mut dp = vec![vec![0; n]; m];
for i in 0..m {
if obstacle_grid[i][0] == 1 {
break;
}
else { dp[i][0] = 1; }
}
for j in 0..n {
if obstacle_grid[0][j] == 1 {
break;
}
else { dp[0][j] = 1; }
}
for i in 1..m {
for j in 1..n {
if obstacle_grid[i][j] == 1 {
continue;
}
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
dp[m-1][n-1]
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
Optimized version:
impl Solution {
pub fn unique_paths_with_obstacles(obstacle_grid: Vec<Vec<i32>>) -> i32 {
let mut dp = vec![0; obstacle_grid[0].len()];
for (i, &v) in obstacle_grid[0].iter().enumerate() {
if v == 0 {
dp[i] = 1;
} else {
break;
}
}
for rows in obstacle_grid.iter().skip(1) {
for j in 0..rows.len() {
if rows[j] == 1 {
dp[j] = 0;
} else if j != 0 {
dp[j] += dp[j - 1];
}
}
}
dp.pop().unwrap()
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# C
int **initDP(int m, int n, int** obstacleGrid) {
int **dp = (int**)malloc(sizeof(int*) * m);
for(int i = 0; i < m; ++i) {
dp[i] = (int*)malloc(sizeof(int) * n);
}
for(int i = 0; i < m; ++i) {
dp[i][0] = 0;
}
for(int j = 0; j < n; ++j) {
dp[0][j] = 0;
}
for(int i = 0; i < m; ++i) {
if(obstacleGrid[i][0]) {
break;
}
dp[i][0] = 1;
}
for(int j = 0; j < n; ++j) {
if(obstacleGrid[0][j]) {
break;
}
dp[0][j] = 1;
}
return dp;
}
int uniquePathsWithObstacles(int** obstacleGrid, int obstacleGridSize, int* obstacleGridColSize) {
int m = obstacleGridSize, n = *obstacleGridColSize;
int **dp = initDP(m, n, obstacleGrid);
for(int i = 1; i < m; ++i) {
for(int j = 1; j < n; ++j) {
if(obstacleGrid[i][j]) {
dp[i][j] = 0;
} else {
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
}
return dp[m-1][n-1];
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
Space optimized version:
int uniquePathsWithObstacles(int** obstacleGrid, int obstacleGridSize, int* obstacleGridColSize) {
int m = obstacleGridSize;
int n = obstacleGridColSize[0];
int *dp = (int*)malloc(sizeof(int) * n);
for (int j = 0; j < n; ++j) {
if (obstacleGrid[0][j] == 1) {
dp[j] = 0;
} else if (j == 0) {
dp[j] = 1;
} else {
dp[j] = dp[j - 1];
}
}
for (int i = 1; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (obstacleGrid[i][j] == 1) {
dp[j] = 0;
} else if (j != 0) {
dp[j] += dp[j - 1];
}
}
}
return dp[n - 1];
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# Scala
object Solution {
import scala.util.control.Breaks._
def uniquePathsWithObstacles(obstacleGrid: Array[Array[Int]]): Int = {
var (m, n) = (obstacleGrid.length, obstacleGrid(0).length)
var dp = Array.ofDim[Int](m, n)
breakable(
for (i <- 0 until m) {
if (obstacleGrid(i)(0) != 1) dp(i)(0) = 1
else break()
}
)
breakable(
for (j <- 0 until n) {
if (obstacleGrid(0)(j) != 1) dp(0)(j) = 1
else break()
}
)
for (i <- 1 until m; j <- 1 until n; if obstacleGrid(i)(j) != 1) {
dp(i)(j) = dp(i - 1)(j) + dp(i)(j - 1)
}
dp(m - 1)(n - 1)
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# C#
public class Solution
{
public int UniquePathsWithObstacles(int[][] obstacleGrid)
{
int m = obstacleGrid.Length;
int n = obstacleGrid[0].Length;
int[,] dp = new int[m, n];
if (obstacleGrid[0][0] == 1 || obstacleGrid[m - 1][n - 1] == 1) return 0;
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i, 0] = 1;
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0, j] = 1;
for (int i = 1; i < m; i++)
{
for (int j = 1; j < n; j++)
{
if (obstacleGrid[i][j] == 1) continue;
dp[i, j] = dp[i - 1, j] + dp[i, j - 1];
}
}
return dp[m - 1, n - 1];
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
