518. Coin Change II

LeetCode Problem Link (opens new window)

Given different denominations of coins and a total amount of money. Write a function to calculate the number of combinations of coins that make up the total amount. Assume that each kind of coin has an infinite number.

Example 1:

• Input: amount = 5, coins = [1, 2, 5]
• Output: 4

Explanation: There are four ways to make up the amount:

• 5=5
• 5=2+2+1
• 5=2+1+1+1
• 5=1+1+1+1+1

Example 2:

• Input: amount = 3, coins = [2]
• Output: 0
• Explanation: Only coins of denomination 2 cannot make up the amount 3.

Example 3:

• Input: amount = 10, coins = [10]
• Output: 1

Notice that:

• 0 <= amount <= 5000
• 1 <= coin <= 5000
• The number of coin types does not exceed 500
• The result fits within a 32-bit signed integer

Two-dimensional DP Explanation

If everyone has completed: Knapsack Theory 01 Knapsack-1 (opens new window), Last Stone Weight II (opens new window) and 0494.Target Sum (opens new window)

You should know similar problems: providing a total, some items, asking if this total can be achieved.

This is a typical knapsack problem!

In this case, the task is to find out how many combinations of items can fill the knapsack with a certain total amount.

Since each kind of coin is infinite, this is a complete knapsack problem.

For those unfamiliar with the complete knapsack, check out: Knapsack Problem Theory Basics Complete Knapsack (opens new window)

However, this problem is different from a pure complete knapsack, as the pure complete knapsack asks for the highest value expected to fill the knapsack, whereas this problem asks for the number of combinations of items that total to a given amount!

Notice how the problem description talks about the number of combinations of coins. Why highlight combinations?

For example, in sample one:

5 = 2 + 2 + 1

5 = 2 + 1 + 2

This counts as one combination, both are 2 2 1.

If asked for permutations, then the above would be two different permutations.

Combinations do not emphasize the order among elements, while permutations do. This concept was also discussed during the backtracking algorithm topic.

Why bring this up? Because it is closely related to the traversal sequence explained below!

This problem is actually quite similar to 0494.Target Sum (opens new window).

0494.Target Sum (opens new window) asks how many ways to fill the knapsack, and this problem asks for the number of combinations.

What's the difference?

Finding how many ways to fill the knapsack is essentially asking for the number of combinations. However, 0494.Target Sum (opens new window) is a 0/1 knapsack, where each type of item only has one piece.

Now let's dive into the following five dynamic programming steps:

1. Define the DP Array and the Meaning of Each Index

Define the two-dimensional DP array dp[i][j]: Using coins with indices [0, i], there are dp[i][j] combinations to fill a knapsack of size j.

Many might wonder, why start with defining the DP array, what is the thought process? This thought process is detailed in Knapsack Theory 01 Knapsack-1 (opens new window) under "Define the DP array and the meaning of each index."

(It is strongly recommended to follow the study order of the programming routine, otherwise, you may not understand the explanation)

2. Determine the Recurrence Relation

Note: The formula derivation here is largely repetitive with 0494.Target Sum (opens new window) and Knapsack Problem Theory Basics Complete Knapsack (opens new window), so the principles won't be repeated, only the differences are explained.

Revisiting Knapsack Theory 01 Knapsack-1 (opens new window), the two-dimensional DP array recurrence relation is:

dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])

In Knapsack Problem Theory Basics Complete Knapsack (opens new window), the complete knapsack two-dimensional DP array recurrence relation was detailed as:

dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i])

What is the distinction between a complete knapsack and a 0/1 knapsack?

It lies in that the 0/1 knapsack uses dp[i - 1][j - weight[i]] + value[i], while the complete knapsack uses dp[i][j - weight[i]] + value[i].

The primary reason is that a complete knapsack allows an infinite quantity of each type of item.

The specifics are explained in Knapsack Problem Theory Basics Complete Knapsack (opens new window). If you've forgotten, do revisit.

I've mentioned before that this problem is the same as 0494.Target Sum (opens new window), the only difference being that 0494.Target Sum (opens new window) is a 0/1 knapsack, while this is a complete knapsack.

In 0494.Target Sum (opens new window), the analysis of how many ways to fill the knapsack, the two-dimensional DP array recurrence relation is: dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i]]

Therefore, in this problem, the recurrence relation is: dp[i][j] = dp[i - 1][j] + dp[i][j - nums[i]], the distinction being between dp[i - 1][j - nums[i]] and dp[i][j - nums[i]].

The ‘therefore’ here omits much of the derivation content, as these contents have been detailed in 0494.Target Sum (opens new window) and Knapsack Problem Theory Basics Complete Knapsack (opens new window).

Here it is not repeated.

The major points of confusion include:

1. How the recurrence formula dp[i][j] = dp[i - 1][j] + dp[i][j - nums[i]] came about is elaborated in 0494.Target Sum (opens new window).

2. Why is it dp[i][j - nums[i]] and not dp[i - 1][j - nums[i]], as in Knapsack Problem Theory Basics Complete Knapsack (opens new window).

3. How to Initialize the DP Array

Here, the top row and leftmost column of the two-dimensional array must be initialized. This is the foundation for the recurrence relation derivation, indicated by the red parts in the diagram.

The first focus should be, what's the value of dp[0][0]?

The knapsack space being 0 means the number of combinations with "item 0" is how many?

It should be 0, but if "item 0" had a value of zero, wouldn't it mean unlimited 0 combinations equal to 0!

Luckily, the problem description states 1 <= coins.length <= 300, so you don't need to worry about item value zero.

How should the top row dp[0][j] be initialized?

The meaning of dp[0][j]: The number of combinations to fill the knapsack of size j using "item 0" (that is, coins[0]). (If the DP array's meaning is unclear, consider first studying 0494.Target Sum (opens new window))

If j is divisible by item 0, there's one combination to fill it.

Initialization code:

for (int j = 0; j <= bagSize; j++) {
    if (j % coins[0] == 0) dp[0][j] = 1;
}

How is the left column initialized?

The meaning of dp[i][0]: The number of combinations to fill a knapsack of capacity 0 with item i (that is, coins[i]).

There is always one way, which is to not pack anything.

So all dp[i][0] are initialized to 1.

4. Determine the Traversal Order

In the two-dimensional DP array's complete knapsack, the order of the two for loops can be either.

Whether to iterate over the knapsack first or the items first, both are fine.

The reason is the same as in Knapsack Theory 01 Knapsack-1 (opens new window) under "Traversal Order."

5. Print the DP Array

Take, for example, amount = 5, coins = [2, 3, 5]:

The dp array should be like this:

1 0 1 0 1 0
1 0 1 1 1 1
1 0 1 1 1 2

Code Implementation:

class Solution {
public:
    int change(int amount, vector<int>& coins) {
        int bagSize = amount;

        vector<vector<uint64_t>> dp(coins.size(), vector<uint64_t>(bagSize + 1, 0));

        // Initialize the top row
        for (int j = 0; j <= bagSize; j++) {
            if (j % coins[0] == 0) dp[0][j] = 1;
        }
        // Initialize the left column
        for (int i = 0; i < coins.size(); i++) {
            dp[i][0] = 1;
        }
        // The order of the subsequent traversal of rows and columns can be reversed
        for (int i = 1; i < coins.size(); i++) { // Row, iterate through items
            for (int j = 0; j <= bagSize; j++) { // Column, iterate through the knapsack
                if (coins[i] > j) dp[i][j] = dp[i - 1][j]; 
                else dp[i][j] = dp[i - 1][j] +  dp[i][j - coins[i]];
            }
        }
        return dp[coins.size() - 1][bagSize];
    }
};

One-dimensional DP Explanation

1. Define the DP Array and the Meaning of Each Index

dp[j]: The number of combinations for achieving the total amount j is dp[j].

2. Determine the Recurrence Relation

The two-dimensional dp recurrence formula for this problem: dp[i][j] = dp[i - 1][j] + dp[i][j - coins[i]]

Compressing it to one dimension: dp[j] += dp[j - coins[i]]

This recurrence formula should be familiar, as it was explained when discussing 0/1 knapsack problems in 0494.Target Sum (opens new window), which involve finding how many ways there are to fill the knapsack, encapsulating the formula: dp[j] += dp[j - nums[i]]

3. How to Initialize the DP Array

The method to fill a knapsack with a capacity of 0 is 1, which is to pack nothing, so dp[0] = 1.

4. Determine the Traversal Order

In this problem, do we use an outer for-loop to iterate over items (coins) and an inner for-loop to iterate over the knapsack (total amount), or the other way around?

In Knapsack Problem Theory Basics Complete Knapsack (opens new window), it's shown that either order is fine in a complete knapsack.

But here, that's not the case!

Because a pure complete knapsack asks how much must be filled, regardless of the order of the elements, whether ordered or not!

This problem, however, requires counting the number of combinations, where element order specifically isn't emphasized.

So while a pure complete knapsack can determine if it's possible to achieve without worrying about how, this problem requires counting the number of possible arrangements, and each is considered a combination.

In this problem, the order of the two for-loops does matter.

Let’s first see what happens when the outer loop iterates through items (coins) and the inner loop iterates through the knapsack (total amount).

for (int i = 0; i < coins.size(); i++) { // Iterate through items
    for (int j = coins[i]; j <= amount; j++) { // Iterate through knapsack capacity
        dp[j] += dp[j - coins[i]];
    }
}

Suppose: coins[0] = 1, coins[1] = 5.

Here, by first including 1 in the calculation and then including 5, we only calculate combinations like {1, 5}. Combinations like {5, 1} are not included.

Thus, in this traversal order, what's calculated in dp[j] are combinations!

If the two for-loops are reversed, the code would be:

for (int j = 0; j <= amount; j++) { // Iterate through knapsack capacity
    for (int i = 0; i < coins.size(); i++) { // Iterate through items
        if (j - coins[i] >= 0) dp[j] += dp[j - coins[i]];
    }
}

In this case, each value of knapsack capacity is calculated through both 1 and 5, including both {1, 5} and {5, 1} situations.

Now what's calculated in dp[j] are permutations!

Some may still not be fully understanding this; it's recommended to manually print out the value changes in the dp array for these two approaches and compare them (practice makes perfect)!

5. Example Analysis of the DP Array

Input: amount = 5, coins = [1, 2, 5], the state of the dp array is shown below:

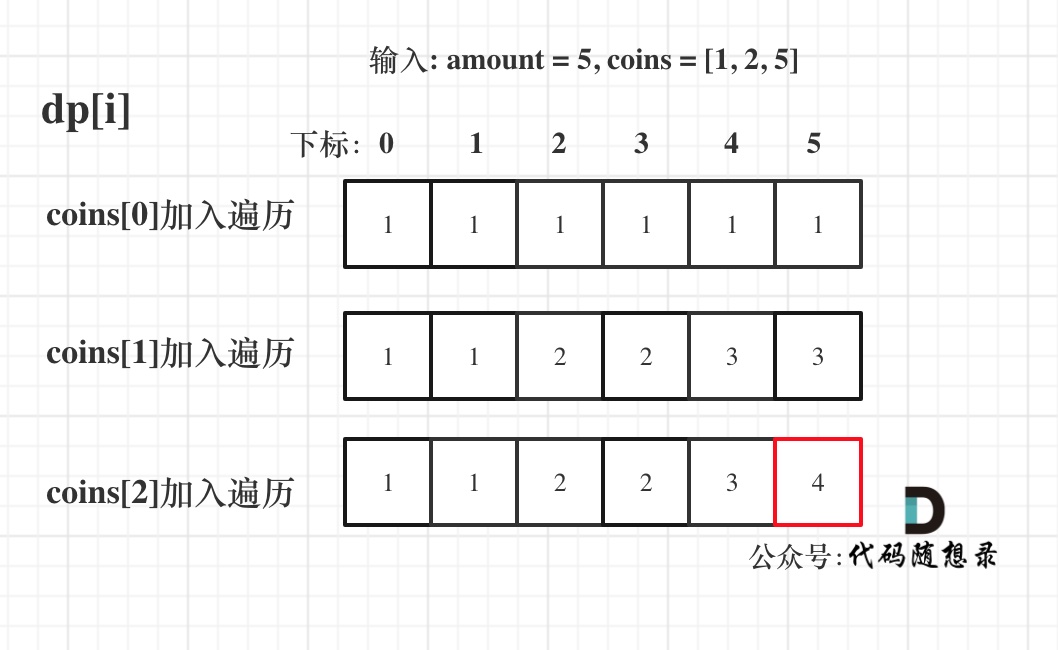
Finally, the result is the value in the red box, dp[amount].

Now, the full C++ code is as follows:

class Solution {
public:
    int change(int amount, vector<int>& coins) {
        vector<uint64_t> dp(amount + 1, 0); // Prevent integer overflow
        dp[0] = 1; // Only one way to make up 0
        for (int i = 0; i < coins.size(); i++) { // Iterate through items
            for (int j = coins[i]; j <= amount; j++) { // Iterate through knapsack
                dp[j] += dp[j - coins[i]];
            }
        }
        return dp[amount]; // Return the count of combinations
    }
};

Some C++ test cases involve adding two numbers that exceed int, so it's necessary to add if (dp[i] < INT_MAX - dp[i - num]) in there.

• Time Complexity: O(mn), where m is amount and n is the length of coins
• Space Complexity: O(m)

To prevent addition data from exceeding int, you can also write:

class Solution {
public:
    int change(int amount, vector<int>& coins) {
        vector<int> dp(amount + 1, 0);
        dp[0] = 1; // Only one way to make up 0
        for (int i = 0; i < coins.size(); i++) { // Iterate through items
            for (int j = coins[i]; j <= amount; j++) { // Iterate through knapsack
                if (dp[j] < INT_MAX - dp[j - coins[i]]) { // Prevent integer overflow
                    dp[j] += dp[j - coins[i]];
                }
            }
        }
        return dp[amount]; // Return the count of combinations
    }
};

Summary

We analyzed from two-dimensional to one-dimensional in this question.

For beginners, it's easier to understand starting from two-dimensional.

Later, I recommend directly mastering the one-dimensional approach, as it's easier to implement once proficient.

In this question, two-dimensional dp mainly requires understanding its relation and difference with the topics Knapsack Theory 01 Knapsack-1 (opens new window), 0494.Target Sum (opens new window), and Knapsack Problem Theory Basics Complete Knapsack (opens new window).

This is the essence of the coding practice's problem-solving sequence.

In the one-dimensional dp of this question, the difficulty lies in understanding the iteration order.

When asking for the number of ways to fill the knapsack, recognizing the loop order is crucial.

If asking for combinations, then iterate over items with the outer loop and iterate over the knapsack with the inner loop.

If asking for permutations, then iterate over the knapsack with the outer loop and iterate over the items with the inner loop.

Some may be puzzled by permutations, but more problems that ask for permutations will be arranged later. When compared, the mystery will become apparent!

Other Language Versions

Java:

class Solution {
    public int change(int amount, int[] coins) {
        // Recurrence relation
        int[] dp = new int[amount + 1];
        // Initialize the dp array, the amount 0 only has one combination, which is not to include anything
        dp[0] = 1;
        for (int i = 0; i < coins.length; i++) {
            for (int j = coins[i]; j <= amount; j++) {
                dp[j] += dp[j - coins[i]];
            }
        }
        return dp[amount];
    }
}

// Version using two-dimensional dp array, easier to understand
class Solution {
    public int change(int amount, int[] coins) {
        int[][] dp = new int[coins.length][amount+1];

        // Initialize boundary values
        for(int i = 0; i < coins.length; i++){
            // First column initial value is 1
            dp[i][0] = 1;
        }
        for(int j = coins[0]; j <= amount; j++){
            // Initialize the first row
            dp[0][j] += dp[0][j-coins[0]];
        }
        
        for(int i = 1; i < coins.length; i++){
            for(int j = 1; j <= amount; j++){
                if(j < coins[i]) dp[i][j] = dp[i-1][j];
                else dp[i][j] = dp[i][j-coins[i]] + dp[i-1][j];
            }
        }

        return dp[coins.length-1][amount];
    }
}

Python:

class Solution:
    def change(self, amount: int, coins: List[int]) -> int:
        dp = [0]*(amount + 1)
        dp[0] = 1
        # Iterate over items
        for i in range(len(coins)):
            # Iterate over knapsack
            for j in range(coins[i], amount + 1):
                dp[j] += dp[j - coins[i]]
        return dp[amount]

Go:

One-dimensional dp

func change(amount int, coins []int) int {
	// Define dp array
	dp := make([]int, amount+1)
	// Initialize, a knapsack with size 0, certainly packs nothing, which is 1 way
	dp[0]  = 1
	// Iteration order
	// Iterate over items
	for i := 0 ;i < len(coins);i++ {
		// Iterate over knapsack
		for j:= coins[i] ; j <= amount ;j++ {
			// Recurrence formula
			dp[j] += dp[j-coins[i]]
		}
	}
	return dp[amount]
}

Two-dimensional dp

func change(amount int, coins []int) int {
    dp := make([][]int, len(coins))
    for i := range dp {
        dp[i] = make([]int, amount + 1)
        dp[i][0] = 1
    }
    for j := coins[0]; j <= amount; j++ {
        dp[0][j] += dp[0][j-coins[0]]
    }
    for i := 1; i < len(coins); i++ {
        for j := 1; j <= amount; j++ {
            if j < coins[i] {
                dp[i][j] = dp[i-1][j]
            } else {
                dp[i][j] = dp[i][j-coins[i]] + dp[i-1][j]
            }
        }
    }
    return dp[len(coins)-1][amount]
}

Rust:

impl Solution {
    pub fn change(amount: i32, coins: Vec<i32>) -> i32 {
        let amount = amount as usize;
        let mut dp = vec![0; amount + 1];
        dp[0] = 1;
        for coin in coins {
            for j in coin as usize..=amount {
                dp[j] += dp[j - coin as usize];
            }
        }
        dp[amount]
    }
}

JavaScript:

const change = (amount, coins) => {
    let dp = Array(amount + 1).fill(0);
    dp[0] = 1;

    for(let i =0; i < coins.length; i++) {
        for(let j = coins[i]; j <= amount; j++) {
            dp[j] += dp[j - coins[i]];
        }
    }

    return dp[amount];
}

TypeScript:

function change(amount: number, coins: number[]): number {
    const dp: number[] = new Array(amount + 1).fill(0);
    dp[0] = 1;
    for (let i = 0, length = coins.length; i < length; i++) {
        for (let j = coins[i]; j <= amount; j++) {
            dp[j] += dp[j - coins[i]];
        }
    }
    return dp[amount];
};

Scala:

object Solution {
  def change(amount: Int, coins: Array[Int]): Int = {
    var dp = new Array[Int](amount + 1)
    dp(0) = 1
    for (i <- 0 until coins.length) {
      for (j <- coins(i) to amount) {
        dp(j) += dp(j - coins(i))
      }
    }
    dp(amount)
  }
}

C

int change(int amount, int* coins, int coinsSize) {
    int dp[amount + 1];
    memset(dp, 0, sizeof (dp));
    dp[0] = 1;
    // Iterate over items
    for(int i = 0; i < coinsSize; i++){
        // Iterate over knapsack
        for(int j = coins[i]; j <= amount; j++){
            dp[j] += dp[j - coins[i]];
        }
    }
    return dp[amount];
}

C#

public class Solution
{
    public int Change(int amount, int[] coins)
    {
        int[] dp = new int[amount + 1];
        dp[0] = 1;
        for (int i = 0; i < coins.Length; i++)
        {
            for (int j = coins[i]; j <= amount; j++)
            {
                if (j >= coins[i])
                    dp[j] += dp[j - coins[i]];
            }
        }
        return dp[amount];
    }
}