# 213. House Robber II
LeetCode Problem Link (opens new window)
You are a professional thief planning to rob houses along the street. Each house contains some amount of money. This place has houses arranged in a circle, which means the first house is next to the last one. Adjacent houses have interconnected security systems, and if two adjacent houses are broken into on the same night, the system will automatically alert.
Given a list of non-negative integers representing the amount of money in each house, calculate the maximum amount of money you can rob without triggering the alarm system.
Example 1:
Input: nums = [2,3,2]
Output: 3
Explanation: You cannot rob house number 1 (amount = 2) and then house number 3 (amount = 2), because they are adjacent.
Example 2:
Input: nums = [1,2,3,1]
Output: 4
Explanation: You can rob house number 1 (amount = 1) and then house number 3 (amount = 3). The maximum amount robbed = 1 + 3 = 4.
Example 3:
Input: nums = [0]
Output: 0
Constraints:
- 1 <= nums.length <= 100
- 0 <= nums[i] <= 1000
# Approach
This problem is similar to 0198.House Robber (opens new window), with the only difference being the houses are arranged in a circle.
For a circular array, there are mainly three cases:
- Case 1: Consider excluding both the first and last elements.
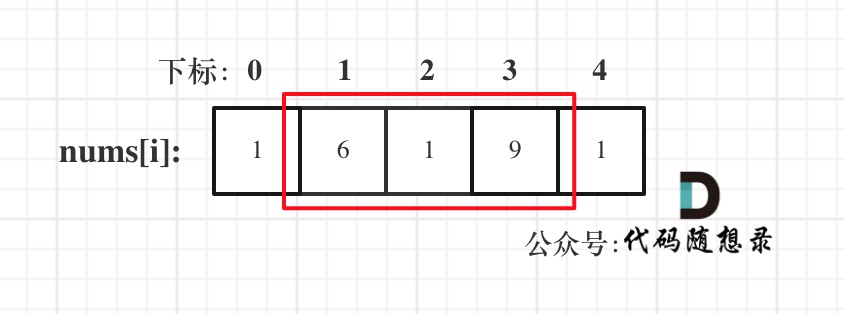
- Case 2: Consider including the first element and excluding the last.
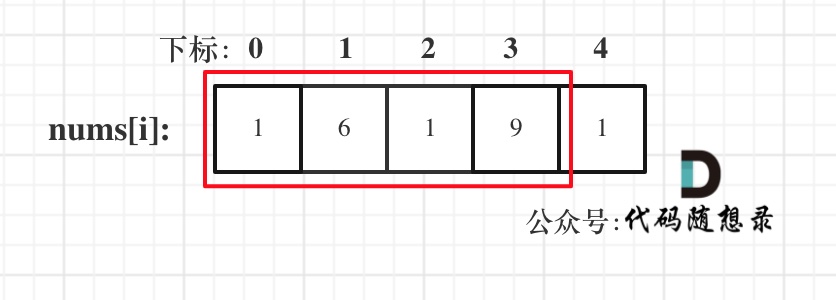
- Case 3: Consider including the last element and excluding the first.
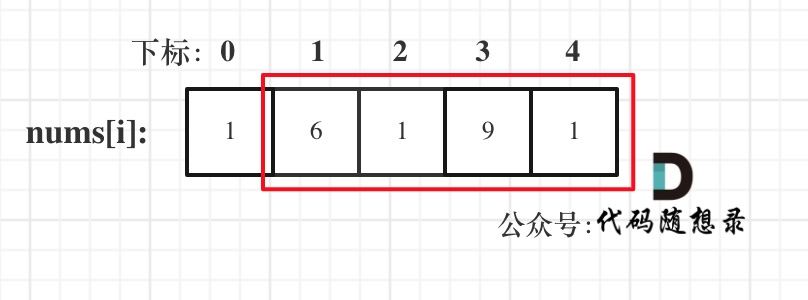
Note that I use the term "consider". For example, in Case 3, although it considers including the last element, it doesn't necessarily have to be selected! For Case 3, choosing nums[1] and nums[3] yields the maximum.
Case 2 and Case 3 both include Case 1, so considering Case 2 and Case 3 suffices.
With this understanding, solving the problem is quite straightforward. The rest is identical to 0198.House Robber (opens new window).
Here is the code:
// Note the use of Case 2 and Case 3 in comments and the extraction of the 198. House Robber solution
class Solution {
public:
int rob(vector<int>& nums) {
if (nums.size() == 0) return 0;
if (nums.size() == 1) return nums[0];
int result1 = robRange(nums, 0, nums.size() - 2); // Case 2
int result2 = robRange(nums, 1, nums.size() - 1); // Case 3
return max(result1, result2);
}
// Logic for 198. House Robber
int robRange(vector<int>& nums, int start, int end) {
if (end == start) return nums[start];
vector<int> dp(nums.size());
dp[start] = nums[start];
dp[start + 1] = max(nums[start], nums[start + 1]);
for (int i = start + 2; i <= end; i++) {
dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
}
return dp[end];
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
- Time Complexity: O(n)
- Space Complexity: O(n)
# Conclusion
The circular aspect adds a layer of complexity. Many solutions do not clarify the difference between "considering houses" and "robbing houses."
This confusion leads to questions like: How does Case 3 include Case 1? The final house in the diagram for Case 3 cannot be robbed for optimal results.
Therefore, I emphasized that Cases 1, 2, and 3 refer to "considering" ranges, and the decisions on which houses to rob are left to the recursive formula.
With this, it becomes clear why Cases 2 and 3 include Case 1.
# Other Language Versions
# Java:
class Solution {
public int rob(int[] nums) {
if (nums == null || nums.length == 0)
return 0;
int len = nums.length;
if (len == 1)
return nums[0];
return Math.max(robAction(nums, 0, len - 1), robAction(nums, 1, len));
}
int robAction(int[] nums, int start, int end) {
int x = 0, y = 0, z = 0;
for (int i = start; i < end; i++) {
y = z;
z = Math.max(y, x + nums[i]);
x = y;
}
return z;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# Python:
class Solution:
def rob(self, nums: List[int]) -> int:
if len(nums) == 0:
return 0
if len(nums) == 1:
return nums[0]
result1 = self.robRange(nums, 0, len(nums) - 2) # Case 2
result2 = self.robRange(nums, 1, len(nums) - 1) # Case 3
return max(result1, result2)
# Logic of 198. House Robber
def robRange(self, nums: List[int], start: int, end: int) -> int:
if end == start:
return nums[start]
prev_max = nums[start]
curr_max = max(nums[start], nums[start + 1])
for i in range(start + 2, end + 1):
temp = curr_max
curr_max = max(prev_max + nums[i], curr_max)
prev_max = temp
return curr_max
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
2D DP
class Solution:
def rob(self, nums: List[int]) -> int:
if len(nums) < 3:
return max(nums)
# Case 2: Do not rob the first house
result1 = self.robRange(nums[:-1])
# Case 3: Do not rob the last house
result2 = self.robRange(nums[1:])
return max(result1, result2)
def robRange(self, nums):
dp = [[0, 0] for _ in range(len(nums))]
dp[0][1] = nums[0]
for i in range(1, len(nums)):
dp[i][0] = max(dp[i - 1])
dp[i][1] = dp[i - 1][0] + nums[i]
return max(dp[-1])
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
Optimized version
class Solution:
def rob(self, nums: List[int]) -> int:
if not nums: # If there are no houses, return 0
return 0
if len(nums) == 1: # If there is only one house, return the money in that house
return nums[0]
# Case 2: Do not rob the first house
prev_max = 0 # Maximum money from the previous house
curr_max = 0 # Maximum money from the current house
for num in nums[1:]:
temp = curr_max # Temporary variable to store the current house's maximum
curr_max = max(prev_max + num, curr_max) # Update the current house's maximum
prev_max = temp # Update the previous house's maximum
result1 = curr_max
# Case 3: Do not rob the last house
prev_max = 0 # Maximum money from the previous house
curr_max = 0 # Maximum money from the current house
for num in nums[:-1]:
temp = curr_max # Temporary variable to store the current house's maximum
curr_max = max(prev_max + num, curr_max) # Update the current house's maximum
prev_max = temp # Update the previous house's maximum
result2 = curr_max
return max(result1, result2)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# Go:
// House Robber II with dynamic programming
// Time complexity O(n), Space complexity O(n)
func rob(nums []int) int {
// If length is 0 or 1, circular or not, it doesn't matter
if len(nums) <= 1 {
return robWithoutCircle(nums)
}
// Otherwise, exclude head or tail and take the maximum
res1 := robWithoutCircle(nums[:len(nums)-1])
res2 := robWithoutCircle(nums[1:])
return max(res1, res2)
}
// Original House Robber version
func robWithoutCircle(nums []int) int {
switch len(nums) {
case 0: return 0
case 1: return nums[0]
}
dp := make([]int, len(nums))
dp[0]=nums[0]
dp[1] = max(nums[0], nums[1])
for i:=2; i<len(nums); i++ {
dp[i] = max(dp[i-1], dp[i-2]+nums[i])
}
return dp[len(nums)-1]
}
func max(a, b int ) int {
if a>b {
return a
}
return b
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
# JavaScript:
var rob = function(nums) {
const n = nums.length
if (n === 0) return 0
if (n === 1) return nums[0]
const result1 = robRange(nums, 0, n - 2)
const result2 = robRange(nums, 1, n - 1)
return Math.max(result1, result2)
};
const robRange = (nums, start, end) => {
if (end === start) return nums[start]
const dp = Array(nums.length).fill(0)
dp[start] = nums[start]
dp[start + 1] = Math.max(nums[start], nums[start + 1])
for (let i = start + 2; i <= end; i++) {
dp[i] = Math.max(dp[i - 2] + nums[i], dp[i - 1])
}
return dp[end]
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# TypeScript:
function rob(nums: number[]): number {
const length: number = nums.length;
if (length === 0) return 0;
if (length === 1) return nums[0];
return Math.max(robRange(nums, 0, length - 2),
robRange(nums, 1, length - 1));
};
function robRange(nums: number[], start: number, end: number): number {
if (start === end) return nums[start];
const dp: number[] = [];
dp[start] = nums[start];
dp[start + 1] = Math.max(nums[start], nums[start + 1]);
for (let i = start + 2; i <= end; i++) {
dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);
}
return dp[end];
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# C
#define max(a, b) ((a) > (b) ? (a) : (b))
// Logic of 198. House Robber
int robRange(int* nums, int start, int end, int numsSize) {
if (end == start) return nums[start];
int dp[numsSize];
dp[start] = nums[start];
dp[start + 1] = max(nums[start], nums[start + 1]);
for (int i = start + 2; i <= end; i++) {
dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
}
return dp[end];
}
int rob(int* nums, int numsSize) {
if (numsSize == 0) return 0;
if (numsSize == 1) return nums[0];
int result1 = robRange(nums, 0, numsSize - 2, numsSize); // Case 2
int result2 = robRange(nums, 1, numsSize - 1, numsSize); // Case 3
return max(result1, result2);
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# Rust:
impl Solution {
pub fn rob(nums: Vec<i32>) -> i32 {
match nums.len() {
1 => nums[0],
_ => Self::rob_range(&nums, 0, nums.len() - 2).max(Self::rob_range(
&nums,
1,
nums.len() - 1,
)),
}
}
pub fn rob_range(nums: &Vec<i32>, start: usize, end: usize) -> i32 {
if start == end {
return nums[start];
}
let mut dp = vec![0; nums.len()];
dp[start] = nums[start];
dp[start + 1] = nums[start].max(nums[start + 1]);
for i in start + 2..=end {
dp[i] = dp[i - 1].max(dp[i - 2] + nums[i]);
}
dp[end]
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
