# 746. Min Cost Climbing Stairs
LeetCode Problem Link (opens new window)
Old Problem Description:
Each index of the array is a step, and the i-th step corresponds to a non-negative cost value cost[i] (index starting from 0).
Every time you climb a step, you need to pay the corresponding cost. Once paid, you can choose to climb one or two steps.
Find the minimum cost to reach the top of the floor. Initially, you can choose to start from the index 0 or index 1.
Example 1:
- Input: cost = [10, 15, 20]
- Output: 15
- Explanation: The minimum cost is to start at cost[1], then take two steps to reach the top, totaling 15.
Example 2:
- Input: cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1]
- Output: 6
- Explanation: The minimum cost is to start at cost[0], go step by step through those 1s, skipping cost[3], and totaling 6.
Constraints:
- The length of
costis in the range [2, 1000]. cost[i]will be an integer, within the range [0, 999].
Previously, the description of this problem was quite vague. It was unclear whether the first step incurs a cost, the last step is free, or the first step is free and the last step incurs a cost.
LeetCode has since revised the problem description. New Problem Description:
You are given an integer array cost where cost[i] is the cost of i-th step on a staircase. Once you pay the cost, you can choose to climb one or two steps.
You can either start from step 0 or step 1.
Your task is to calculate the minimum cost to reach the top of the staircase.

# Idea
(After LeetCode modified the problem statement, I revised the solution accordingly.)
The modified problem statement now makes it clearer. The statement "You can choose to start from the 0th or 1st step" essentially means that jumping to index 0 or index 1 doesn't incur any cost, but beginning from index 0 or index 1 to jump further does incur the cost.
- Define the dp array and the meaning of indices
Dynamic programming requires an array to keep track of states. In this problem, a one-dimensional array dp[i] is sufficient.
Definition of dp[i]: The minimum cost to reach the i-th step is dp[i].
Ensure you have a clear understanding of the dp array's definition!
- Determine the recursive formula
There are two ways to reach dp[i]: from dp[i-1] and dp[i-2].
Jumping to dp[i] from dp[i - 1] requires a cost of dp[i - 1] + cost[i - 1].
Jumping to dp[i] from dp[i - 2] requires a cost of dp[i - 2] + cost[i - 2].
Which path should we choose to reach dp[i]? Naturally, we choose the one with the least cost: dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]).
- Initializing the
dparray
Looking at the recursive formula, dp[i] derives from dp[i - 1] and dp[i - 2]. Initializing all the dp[i] values is not feasible, so initializing dp[0] and dp[1] suffices, as the rest follow from these values.
What should dp[0] be? According to the definition of the dp array, the minimum cost to reach the 0th step is dp[0]. Some might think dp[0] should be cost[0]. For example, if cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1], dp[0] should be 1.
The clarity of the revised problem statement on LeetCode explains why it's modified. As stated in the new problem, "You can choose to start from index 0 or index 1," reaching the zeroth step is free, but moving upwards from index 0 does incur cost[0].
Therefore, initialize with dp[0] = 0 and dp[1] = 0.
- Determine the loop order
Finally, with the recursive formula and initialization done, how should we traverse through the costs?
The sequence of traversal in this problem is quite straightforward, and many skip pondering over this step and jump straight to coding.
Since this involves simulating steps and calculating dp[i] based on dp[i-1] and dp[i-2], traversing the cost array from start to finish will suffice.
For slightly more challenging dynamic programming problems, determining the loop order is not always straightforward. For instance, the 0/1 knapsack problem. Many know it involves two for-loops, one iterating over the items and a nested one over the capacity. But why not traverse the capacity with one loop and nest items inside the other? And why reverse the loop while using a one-dimensional array? These aspects are closely linked to loop order. Rest assured, the knapsack problem will be extensively covered later on!
- Walk through the
dparray with examples
Let's simulate the changes in the dp array with Example 2: cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1].
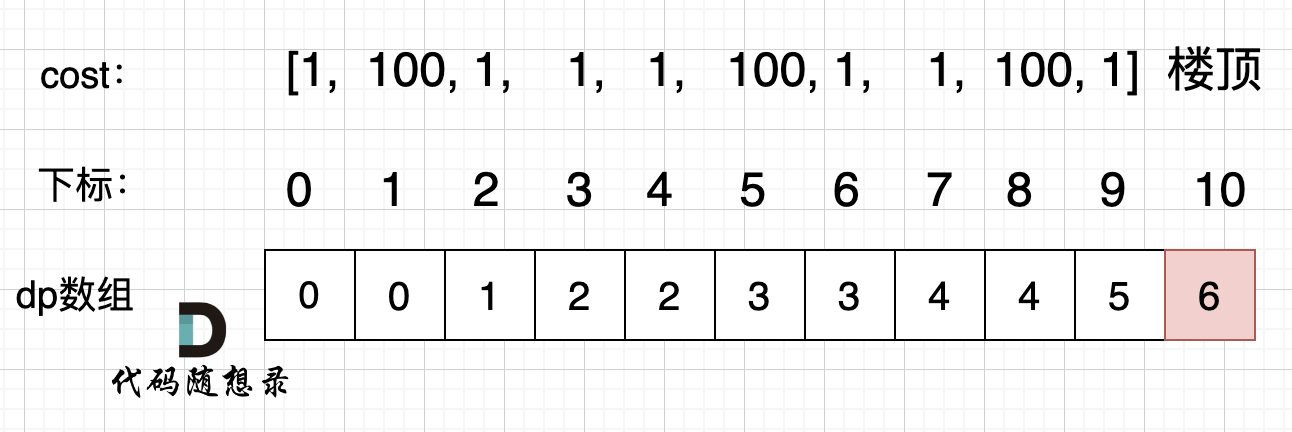
Should you encounter issues with your code, print out the dp array and compare with the walkthrough.
The C++ code for the above analysis is:
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
vector<int> dp(cost.size() + 1);
dp[0] = 0; // Assume the first step is free
dp[1] = 0;
for (int i = 2; i <= cost.size(); i++) {
dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
}
return dp[cost.size()];
}
};
2
3
4
5
6
7
8
9
10
11
12
- Time Complexity: O(n)
- Space Complexity: O(n)
The space complexity can be optimized because dp[i] is derived from the previous two values. Here's the C++ code for that:
// Version 2
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
int dp0 = 0;
int dp1 = 0;
for (int i = 2; i <= cost.size(); i++) {
int dpi = min(dp1 + cost[i - 1], dp0 + cost[i - 2]);
dp0 = dp1; // Record the previous two
dp1 = dpi;
}
return dp1;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
- Time Complexity: O(n)
- Space Complexity: O(1)
In interviews, producing Version 1 should suffice unless the interviewer specifically asks for space optimization, in which case consider Version 2. Version 2 can be a bit tricky. Version 1 is more straightforward.
# Extension
For the old LeetCode description, if the first step includes a cost and the last step does not, then the code for it is written like this, which can also pass:
// Version 1
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
vector<int> dp(cost.size());
dp[0] = cost[0]; // Initial step incurs a cost
dp[1] = cost[1];
for (int i = 2; i < cost.size(); i++) {
dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i];
}
// The last step can be seen as cost-free, hence taking the minimum of the last two
return min(dp[cost.size() - 1], dp[cost.size() - 2]);
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
Of course, if your understanding of dynamic programming is shallow, then skipping the extra content may prevent confusion.
# Summary
You might notice that this problem is slightly more challenging compared to yesterday's 0070.Climbing Stairs (opens new window) but follows a similar thought process.
From 0509.Fibonacci Number (opens new window) to 0070.Climbing Stairs (opens new window) and now to this problem, do you feel the progressive learning curve?
Whenever I start with a series, I receive feedback saying the problems are too easy and need a challenge, while others mention it's becoming difficult to keep up.
However, each problem is chosen with a purpose. Even simple ones practice methodology, and the difficulty gradually increases, building upon each other.
But I could easily pick a random difficult problem to explain, which saves a lot of effort—no order needed, just based on mood.
The hard part is arranging the problems in the right sequence, progressing step by step, and interconnecting them with a unified methodology, so please follow my pace.
# Other Language Versions
Below are solution versions in other languages, mainly based on old LeetCode solutions. You're welcome to submit corrections on Github (opens new window).
# Java
// Method 1: No cost for the first step
class Solution {
public int minCostClimbingStairs(int[] cost) {
int len = cost.length;
int[] dp = new int[len + 1];
// Start from index 0 or 1, hence no cost initially
dp[0] = 0;
dp[1] = 0;
// Calculate minimal cost to each step
for (int i = 2; i <= len; i++) {
dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
}
return dp[len];
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// Method 2: Cost for the first step
class Solution {
public int minCostClimbingStairs(int[] cost) {
int[] dp = new int[cost.length];
dp[0] = cost[0];
dp[1] = cost[1];
for (int i = 2; i < cost.length; i++) {
dp[i] = Math.min(dp[i - 1], dp[i - 2]) + cost[i];
}
// Final step incurs no cost, hence take the minimum of the two preceding steps
return Math.min(dp[cost.length - 1], dp[cost.length - 2]);
}
}
2
3
4
5
6
7
8
9
10
11
12
13
// Space optimization: Use three variables instead of an array
class Solution {
public int minCostClimbingStairs(int[] cost) {
// These variables represent minimal costs for two steps before, one step before, and current step.
int beforeTwoCost = 0, beforeOneCost = 0, currentCost = 0;
// Start from index 2 since index 0 and 1 cost nothing, traverse until cost.length for the final jump
for (int i = 2; i <= cost.length; i++) {
// Traverse cost[i-1], won't go out of bounds
currentCost = Math.min(beforeOneCost + cost[i - 1], beforeTwoCost + cost[i - 2]);
beforeTwoCost = beforeOneCost;
beforeOneCost = currentCost;
}
return currentCost;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# Python
Dynamic Programming (Version 1)
class Solution:
def minCostClimbingStairs(self, cost: List[int]) -> int:
dp = [0] * (len(cost) + 1)
dp[0] = 0 # Initial value, indicating no cost from start
dp[1] = 0 # Initial value, indicating no cost on the first step
for i in range(2, len(cost) + 1):
# On the i-th step, choose between the previous step (i-1) or the step before last (i-2); add the cost and update the dp array
dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])
return dp[len(cost)] # Return minimal cost to reach the top
2
3
4
5
6
7
8
9
10
11
Dynamic Programming (Version 2)
class Solution:
def minCostClimbingStairs(self, cost: List[int]) -> int:
dp0 = 0 # Initial value, indicating no cost from start
dp1 = 0 # Initial value, indicating no cost on the first step
for i in range(2, len(cost) + 1):
# On the i-th step, choose between the previous step (i-1) or the step before last (i-2); add the cost
dpi = min(dp1 + cost[i - 1], dp0 + cost[i - 2])
dp0 = dp1 # Update dp0 to be the value of the previous step, i.e., dp1 from last iteration
dp1 = dpi # Update dp1 to the minimal cost of the current step
return dp1 # Return minimal cost to reach the top
2
3
4
5
6
7
8
9
10
11
12
13
Dynamic Programming (Version 3)
class Solution:
def minCostClimbingStairs(self, cost: List[int]) -> int:
dp = [0] * len(cost)
dp[0] = cost[0] # First step incurs a cost
dp[1] = cost[1]
for i in range(2, len(cost)):
dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i]
# Final step can be understood as free, so take the minimum of the last two steps
return min(dp[-1], dp[-2])
2
3
4
5
6
7
8
9
Dynamic Programming (Version 4)
class Solution:
def minCostClimbingStairs(self, cost: List[int]) -> int:
n = len(cost)
prev_1 = cost[0] # Minimal cost of the step before last
prev_2 = cost[1] # Minimal cost of the step last
for i in range(2, n):
current = min(prev_1, prev_2) + cost[i] # Minimal cost at current step
prev_1, prev_2 = prev_2, current # Update costs of the last two steps
return min(prev_1, prev_2) # The final step can be free, take the minimum of the last two
2
3
4
5
6
7
8
9
# Go
func minCostClimbingStairs(cost []int) int {
f := make([]int, len(cost) + 1)
f[0], f[1] = 0, 0
for i := 2; i <= len(cost); i++ {
f[i] = min(f[i-1] + cost[i-1], f[i-2] + cost[i-2])
}
return f[len(cost)]
}
func min(a, b int) int {
if a < b {
return a
}
return b
}
2
3
4
5
6
7
8
9
10
11
12
13
14
Version 2 Thought: dp[i] indicates the minimum cost from starting to jump at step i Recursion Formula: If i<n: dp[i] = min(dp[i-1],dp[i-2])+cost[i] If i==n: dp[i] = min(dp[i-1],dp[i-2]) (Climbing to the top)
func minCostClimbingStairs(cost []int) int {
n := len(cost)
dp := make([]int, n+1)
dp[0], dp[1] = cost[0], cost[1]
for i := 2; i <= n; i++ {
if i < n {
dp[i] = min(dp[i-1], dp[i-2]) + cost[i]
} else {
dp[i] = min(dp[i-1], dp[i-2])
}
}
return dp[n]
}
func min(a, b int) int {
if a < b {
return a
}
return b
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# JavaScript
var minCostClimbingStairs = function(cost) {
const dp = [0, 0]
for (let i = 2; i <= cost.length; ++i) {
dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])
}
return dp[cost.length]
};
2
3
4
5
6
7
No dp array used
var minCostClimbingStairs = function(cost) {
let dpBefore = 0,
dpAfter = 0
for(let i = 2;i <= cost.length;i++){
let dpi = Math.min(dpBefore + cost[i - 2],dpAfter + cost[i - 1])
dpBefore = dpAfter
dpAfter = dpi
}
return dpAfter
};
2
3
4
5
6
7
8
9
10
# TypeScript
function minCostClimbingStairs(cost: number[]): number {
const dp = [0, 0]
for (let i = 2; i <= cost.length; i++) {
dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])
}
return dp[cost.length]
}
2
3
4
5
6
7
No dp array used
function minCostClimbingStairs(cost: number[]): number {
let dpBefore = 0,
dpAfter = 0
for (let i = 2; i <= cost.length; i++) {
let dpi = Math.min(dpBefore + cost[i - 2], dpAfter + cost[i - 1])
dpBefore = dpAfter
dpAfter = dpi
}
return dpAfter
}
2
3
4
5
6
7
8
9
10
# Rust
impl Solution {
pub fn min_cost_climbing_stairs(cost: Vec<i32>) -> i32 {
let mut dp = vec![0; cost.len() + 1];
for i in 2..=cost.len() {
dp[i] = (dp[i - 1] + cost[i - 1]).min(dp[i - 2] + cost[i - 2]);
}
dp[cost.len()]
}
}
2
3
4
5
6
7
8
9
No dp array used
impl Solution {
pub fn min_cost_climbing_stairs(cost: Vec<i32>) -> i32 {
let (mut dp_before, mut dp_after) = (0, 0);
for i in 2..=cost.len() {
let dpi = (dp_before + cost[i - 2]).min(dp_after + cost[i - 1]);
dp_before = dp_after;
dp_after = dpi;
}
dp_after
}
}
2
3
4
5
6
7
8
9
10
11
# C
#include <math.h>
int minCostClimbingStairs(int *cost, int costSize) {
int dp[costSize + 1];
dp[0] = dp[1] = 0;
for (int i = 2; i <= costSize; i++) {
dp[i] = fmin(dp[i - 2] + cost[i - 2], dp[i - 1] + cost[i - 1]);
}
return dp[costSize];
}
2
3
4
5
6
7
8
9
No dp array used
#include <math.h>
int minCostClimbingStairs(int *cost, int costSize) {
int dpBefore = 0, dpAfter = 0;
for (int i = 2; i <= costSize; i++) {
int dpi = fmin(dpBefore + cost[i - 2], dpAfter + cost[i - 1]);
dpBefore = dpAfter;
dpAfter = dpi;
}
return dpAfter;
}
2
3
4
5
6
7
8
9
10
# Scala
object Solution {
def minCostClimbingStairs(cost: Array[Int]): Int = {
var dp = new Array[Int](cost.length)
dp(0) = cost(0)
dp(1) = cost(1)
for (i <- 2 until cost.length) {
dp(i) = math.min(dp(i - 1), dp(i - 2)) + cost(i)
}
math.min(dp(cost.length - 1), dp(cost.length - 2))
}
}
2
3
4
5
6
7
8
9
10
11
Version 2 Thought: dp[i] indicates the minimum cost from starting to jump at step i-1 Recursion Formula: dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])
object Solution {
def minCostClimbingStairs(cost: Array[Int]): Int = {
var dp = new Array[Int](cost.length + 1)
for (i <- 2 until cost.length + 1) {
dp(i) = math.min(dp(i - 1) + cost(i - 1), dp(i - 2) + cost(i - 2))
}
dp(cost.length)
}
}
2
3
4
5
6
7
8
9
# C#
public class Solution
{
public int MinCostClimbingStairs(int[] cost)
{
int[] dp=new int[2] { cost[0], cost[1] };
for (int i = 2; i < cost.Length; i++)
{
int temp = Math.Min(dp[0], dp[1])+cost[i];
dp[0]=dp[1];
dp[1]=temp;
}
return Math.Min(dp[0],dp[1]);
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
