# 139. Word Break
LeetCode problem link (opens new window)
Given a non-empty string s and a list of non-empty words wordDict, determine if s can be segmented into a space-separated sequence of one or more dictionary words.
Note:
- The same word in the dictionary may be reused multiple times in segmentation.
- You may assume the dictionary does not contain duplicate words.
Example 1:
- Input:
s = "leetcode",wordDict = ["leet", "code"] - Output:
true - Explanation: Return true because
"leetcode"can be segmented as"leet code".
Example 2:
- Input:
s = "applepenapple",wordDict = ["apple", "pen"] - Output:
true - Explanation: Return true because
"applepenapple"can be segmented as"apple pen apple". Note that you are allowed to reuse a dictionary word.
Example 3:
- Input:
s = "catsandog",wordDict = ["cats", "dog", "sand", "and", "cat"] - Output:
false
# Thought Process
Reflecting on this problem, you might recall a problem we previously discussed under the backtracking topic: 0131.Palindrome Partitioning (opens new window), which involves enumerating all possible palindrome partitions of a string.
0131.Palindrome Partitioning (opens new window): It enumerates all possible partitions to check if substrings are palindromes.
The current task is similar but involves enumerating all segmentations to verify if the substrings appear in the dictionary.
Here's the backtracking method in C++ code:
class Solution {
private:
bool backtracking (const string& s, const unordered_set<string>& wordSet, int startIndex) {
if (startIndex >= s.size()) {
return true;
}
for (int i = startIndex; i < s.size(); i++) {
string word = s.substr(startIndex, i - startIndex + 1);
if (wordSet.find(word) != wordSet.end() && backtracking(s, wordSet, i + 1)) {
return true;
}
}
return false;
}
public:
bool wordBreak(string s, vector<string>& wordDict) {
unordered_set<string> wordSet(wordDict.begin(), wordDict.end());
return backtracking(s, wordSet, 0);
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
- Time Complexity: O(2^n), since each word has two states: split or not split.
- Space Complexity: O(n), for recursion system call stack space.
However, the above code will obviously lead to a time limit exceeded error for certain test cases:
"aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaab"
["a","aa","aaa","aaaa","aaaaa","aaaaaa","aaaaaaa","aaaaaaaa","aaaaaaaaa","aaaaaaaaaa"]
2
Many calculations are repeated during recursion and can be optimized by storing calculated results in an array.
This technique is known as memoized recursion, which we've discussed multiple times.
Using a memory array to store results from each startIndex calculation avoids repeated computation. If memory[startIndex] has already been assigned, we simply use the stored result.
Here's the C++ code:
class Solution {
private:
bool backtracking (const string& s,
const unordered_set<string>& wordSet,
vector<bool>& memory,
int startIndex) {
if (startIndex >= s.size()) {
return true;
}
// If memory[startIndex] is not an initial value, return the result from memory[startIndex]
if (!memory[startIndex]) return memory[startIndex];
for (int i = startIndex; i < s.size(); i++) {
string word = s.substr(startIndex, i - startIndex + 1);
if (wordSet.find(word) != wordSet.end() && backtracking(s, wordSet, memory, i + 1)) {
return true;
}
}
memory[startIndex] = false; // Record that the substring starting at startIndex cannot be segmented
return false;
}
public:
bool wordBreak(string s, vector<string>& wordDict) {
unordered_set<string> wordSet(wordDict.begin(), wordDict.end());
vector<bool> memory(s.size(), 1); // -1 means uninitialized state
return backtracking(s, wordSet, memory, 0);
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
This still has a time complexity of O(2^n) but shows remarkable optimization for certain inputs that would otherwise cause a timeout.
This code can be accepted, but backtracking is not the main algorithm here—the main focus is on dynamic programming!
# Dynamic Programming Approach (Knapsack Problem)
Words are like items, the string s is like a knapsack, and determining if words can form the string s is like asking if items can fill the knapsack.
The same word can be reused for segmentation, indicating a complete knapsack problem!
The dynamic programming process:
Define dp array and index meaning
dp[i]: If the string length isi,dp[i]istrueif it can be segmented into one or more dictionary words.Recursive formula
If
dp[j]istrueand the substring[j, i]appears in the dictionary, thendp[i]istrue(forj < i).Formula: if (substring
[j, i]is in dictionary &&dp[j]istrue) thendp[i] = true.Initialize dp array
Since the formula depends on
dp[j]being true,dp[0]must be true to proceed. If not initialized, all subsequent values would be false.Does
dp[0]have significance?dp[0]indicates an empty string is considered valid, but the problem specifies a non-empty string "s", so test data won't have a case wherei=0. Therefore,dp[0]is initialized to true just to derive the formula.Indexes other than
0will be initialized to false, being overwritten if they can be segmented into dictionary words.Determine traversal order
It's a complete knapsack problem as mentioned. The loop order of items and knapsack needs consideration.
For combination counts, outer loop goes through items, inner loop through knapsack.
For permutation counts, outer loop goes through knapsack, inner loop through items.
In summary:
Combination count: 0518.Coin Change II (opens new window)
Permutation count: 377. Combination Sum IV (opens new window) and 0070.Climbing Stairs Complete Knapsack Version (opens new window)
Minimum count: 322.Coin Change (opens new window) and 279.Perfect Squares (opens new window)
In this problem, we seek permutations because: consider
s = "applepenapple",wordDict = ["apple", "pen"]. If "apple", "pen" are items, the sequence "apple" + "pen" + "apple" is necessary to form "applepenapple". Thus, order matters.So, loop through knapsack first, then items.
Example for
dp[i]calculationFor input:
s = "leetcode",wordDict = ["leet", "code"], the dp state is:
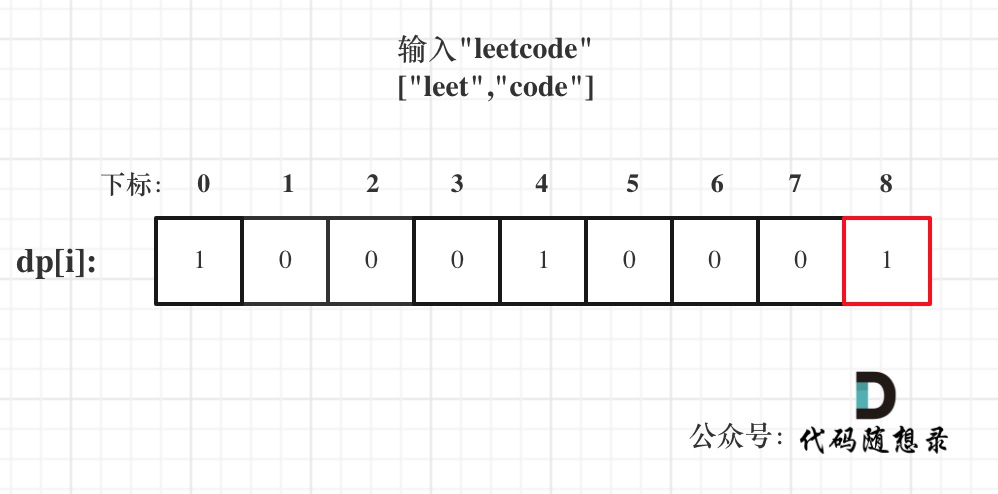
The result is found in dp[s.size()].
With the analysis complete, here's the C++ code:
class Solution {
public:
bool wordBreak(string s, vector<string>& wordDict) {
unordered_set<string> wordSet(wordDict.begin(), wordDict.end());
vector<bool> dp(s.size() + 1, false);
dp[0] = true;
for (int i = 1; i <= s.size(); i++) { // Traverse knapsack
for (int j = 0; j < i; j++) { // Traverse items
string word = s.substr(j, i - j); //substr(start position, number of characters)
if (wordSet.find(word) != wordSet.end() && dp[j]) {
dp[i] = true;
}
}
}
return dp[s.size()];
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
- Time Complexity: O(n^3), due to
substrreturning a substring copy with O(n) complexity (wherenis the substring length). - Space Complexity: O(n)
# Further Exploration
Regarding traversal order, let's explain why iterating over items before the knapsack does not work.
Here's the code for iterating over items first:
class Solution {
public:
bool wordBreak(string s, vector<string>& wordDict) {
unordered_set<string> wordSet(wordDict.begin(), wordDict.end());
vector<bool> dp(s.size() + 1, false);
dp[0] = true;
for (int j = 0; j < wordDict.size(); j++) { // Items
for (int i = wordDict[j].size(); i <= s.size(); i++) { // Knapsack
string word = s.substr(i - wordDict[j].size(), wordDict[j].size());
if (word == wordDict[j] && dp[i - wordDict[j].size()]) {
dp[i] = true;
}
}
}
return dp[s.size()];
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Using: s = "applepenapple", wordDict = ["apple", "pen"], the dp array looks like:
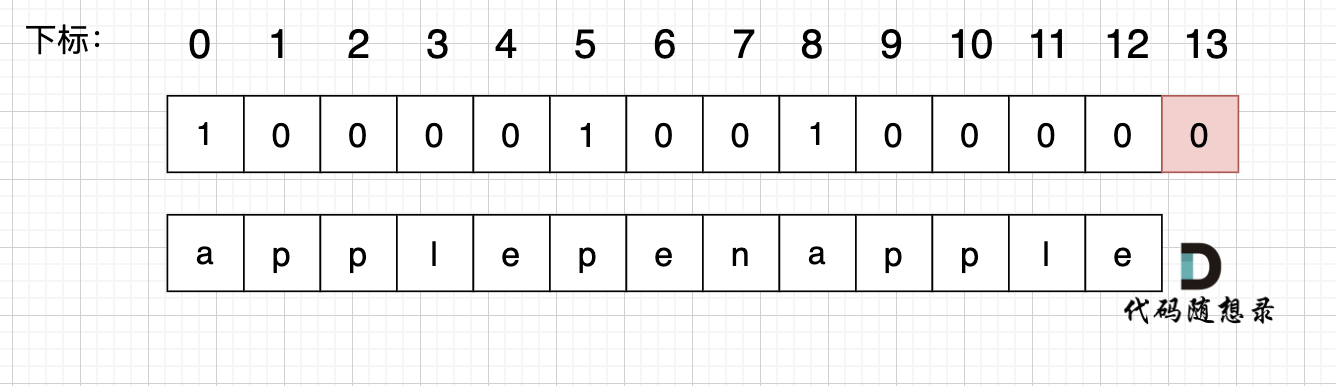
Finally dp[s.size()] = 0 i.e., dp[13] = 0, instead of 1, since "apple" traversed before "pen" leaves dp[8] unassigned as 1. Hence, dp[13] remains 0.
If "apple" is traversed first, then "pen", dp[8] would be 1. Finally, with "apple" traversed again, dp[13] becomes 1.
Try running the above code on LeetCode to clearly understand the recursive logic and dp array changes during each step of the process.
# Summary
This problem is highly similar to the backtracking problem 0131.Palindrome Partitioning (opens new window). Thus, a backtracking solution is provided.
A slight analysis reveals it is a complete knapsack problem requiring ordering of items.
# Other Language Versions
# Java:
class Solution {
public boolean wordBreak(String s, List<String> wordDict) {
HashSet<String> set = new HashSet<>(wordDict);
boolean[] valid = new boolean[s.length() + 1];
valid[0] = true;
for (int i = 1; i <= s.length(); i++) {
for (int j = 0; j < i && !valid[i]; j++) {
if (set.contains(s.substring(j, i)) && valid[j]) {
valid[i] = true;
}
}
}
return valid[s.length()];
}
}
// Another knapsack solution approach
class Solution {
public boolean wordBreak(String s, List<String> wordDict) {
boolean[] dp = new boolean[s.length() + 1];
dp[0] = true;
for (int i = 1; i <= s.length(); i++) {
for (String word : wordDict) {
int len = word.length();
if (i >= len && dp[i - len] && word.equals(s.substring(i - len, i))) {
dp[i] = true;
break;
}
}
}
return dp[s.length()];
}
}
// Backtracking + Memoization
class Solution {
private Set<String> set;
private int[] memo;
public boolean wordBreak(String s, List<String> wordDict) {
memo = new int[s.length()];
set = new HashSet<>(wordDict);
return backtracking(s, 0);
}
public boolean backtracking(String s, int startIndex) {
if (startIndex == s.length()) {
return true;
}
if (memo[startIndex] == -1) {
return false;
}
for (int i = startIndex; i < s.length(); i++) {
String sub = s.substring(startIndex, i + 1);
if (!set.contains(sub)) {
continue;
}
if (backtracking(s, i + 1)) return true;
}
memo[startIndex] = -1;
return false;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
# Python:
Backtracking
class Solution:
def backtracking(self, s: str, wordSet: set[str], startIndex: int) -> bool:
if startIndex >= len(s):
return True
for i in range(startIndex, len(s)):
word = s[startIndex:i + 1]
if word in wordSet and self.backtracking(s, wordSet, i + 1):
return True
return False
def wordBreak(self, s: str, wordDict: List[str]) -> bool:
wordSet = set(wordDict)
return self.backtracking(s, wordSet, 0)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
DP (Version 1)
class Solution:
def wordBreak(self, s: str, wordDict: List[str]) -> bool:
wordSet = set(wordDict)
n = len(s)
dp = [False] * (n + 1)
dp[0] = True
for i in range(1, n + 1):
for j in range(i):
if dp[j] and s[j:i] in wordSet:
dp[i] = True
break
return dp[n]
2
3
4
5
6
7
8
9
10
11
12
13
14
15
DP (Version 2)
class Solution:
def wordBreak(self, s: str, wordDict: List[str]) -> bool:
dp = [False]*(len(s) + 1)
dp[0] = True
for j in range(1, len(s) + 1):
for word in wordDict:
if j >= len(word):
dp[j] = dp[j] or (dp[j - len(word)] and word == s[j - len(word):j])
return dp[len(s)]
2
3
4
5
6
7
8
9
DP (Pruning)
class Solution(object):
def wordBreak(self, s, wordDict):
wordDict.sort(key=lambda x: len(x))
n = len(s)
dp = [False] * (n + 1)
dp[0] = True
for i in range(1, n + 1):
for word in wordDict:
if len(word) > i:
break
dp[i] = dp[i] or (dp[i - len(word)] and s[i - len(word): i] == word)
return dp[-1]
2
3
4
5
6
7
8
9
10
11
12
13
14
# Go:
func wordBreak(s string,wordDict []string) bool {
wordDictSet := make(map[string]bool)
for _, w := range wordDict {
wordDictSet[w] = true
}
dp := make([]bool, len(s)+1)
dp[0] = true
for i := 1; i <= len(s); i++ {
for j := 0; j < i; j++ {
if dp[j] && wordDictSet[s[j:i]] {
dp[i] = true
break
}
}
}
return dp[len(s)]
}
// Convert to determine the number of ways to fill the first several characters of knapsack s
func wordBreak(s string, wordDict []string) bool {
dp := make([]int, len(s)+1)
dp[0] = 1
for i := 0; i <= len(s); i++ { // Knapsack
for j := 0; j < len(wordDict); j++ { // Items
if i >= len(wordDict[j]) && wordDict[j] == s[i-len(wordDict[j]):i] {
dp[i] += dp[i-len(wordDict[j])]
}
}
}
return dp[len(s)] > 0
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# JavaScript:
const wordBreak = (s, wordDict) => {
let dp = Array(s.length + 1).fill(false);
dp[0] = true;
for(let i = 0; i <= s.length; i++){
for(let j = 0; j < wordDict.length; j++) {
if(i >= wordDict[j].length) {
if(s.slice(i - wordDict[j].length, i) === wordDict[j] && dp[i - wordDict[j].length]) {
dp[i] = true
}
}
}
}
return dp[s.length];
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# TypeScript:
Dynamic Programming
function wordBreak(s: string, wordDict: string[]): boolean {
const dp: boolean[] = new Array(s.length + 1).fill(false);
dp[0] = true;
for (let i = 1; i <= s.length; i++) {
for (let j = 0; j < i; j++) {
const tempStr: string = s.slice(j, i);
if (wordDict.includes(tempStr) && dp[j] === true) {
dp[i] = true;
break;
}
}
}
return dp[s.length];
};
2
3
4
5
6
7
8
9
10
11
12
13
14
Backtracking with Memoization
function wordBreak(s: string, wordDict: string[]): boolean {
const memory: boolean[] = [];
return backTracking(s, wordDict, 0, memory);
function backTracking(s: string, wordDict: string[], startIndex: number, memory: boolean[]): boolean {
if (startIndex >= s.length) return true;
if (memory[startIndex] === false) return false;
for (let i = startIndex + 1, length = s.length; i <= length; i++) {
const str: string = s.slice(startIndex, i);
if (wordDict.includes(str) && backTracking(s, wordDict, i, memory))
return true;
}
memory[startIndex] = false;
return false;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# C
bool wordBreak(char* s, char** wordDict, int wordDictSize) {
int len = strlen(s);
bool dp[len + 1];
memset(dp, false, sizeof (dp));
dp[0] = true;
for (int i = 1; i < len + 1; ++i) {
for(int j = 0; j < wordDictSize; j++){
int wordLen = strlen(wordDict[j]);
int k = i - wordLen;
if(k < 0){
continue;
}
dp[i] = (dp[k] && !strncmp(s + k, wordDict[j], wordLen)) || dp[i];
}
}
return dp[len];
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# Rust:
impl Solution {
pub fn word_break(s: String, word_dict: Vec<String>) -> bool {
let mut dp = vec![false; s.len() + 1];
dp[0] = true;
for i in 1..=s.len() {
for j in 0..i {
if word_dict.iter().any(|word| *word == s[j..i]) && dp[j] {
dp[i] = true;
}
}
}
dp[s.len()]
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
