# 70. Climbing Stairs
LeetCode Problem Link (opens new window)
Suppose you're climbing stairs. It takes n steps to reach the top.
Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?
Note: Given n is a positive integer.
Example 1:
- Input: 2
- Output: 2
- Explanation: There are two ways to climb to the top.
- 1 step + 1 step
- 2 steps
Example 2:
- Input: 3
- Output: 3
- Explanation: There are three ways to climb to the top.
- 1 step + 1 step + 1 step
- 1 step + 2 steps
- 2 steps + 1 step
# Solution
If you haven't encountered this problem before, it might seem quite challenging. However, by examining several examples, you can identify a pattern.
There's one way to reach the first step and two ways to reach the second step.
Then, from the first step, you can jump two steps to reach the third step, and from the second step, you can jump one step to reach the third step.
This means the state of reaching the third step can be deduced from the states of reaching the first and second steps, indicating that dynamic programming can be applied.
Let's analyze the problem using the five-step dynamic programming approach:
We can define a one-dimensional array to record the state of different levels.
- Determine the dp array and the meaning of its index.
dp[i]: There are dp[i] ways to climb to the i-th step.
- Establish the recurrence relation.
How can we derive dp[i]?
From the definition of dp[i], it can be derived in two ways.
First, from dp[i - 1]. There are dp[i - 1] ways to the i-1 step, and by taking one more step, we reach dp[i].
Second, from dp[i - 2]. There are dp[i - 2] ways to the i-2 step, and by taking two more steps, we reach dp[i].
Thus, dp[i] is the sum of dp[i - 1] and dp[i - 2]!
So, dp[i] = dp[i - 1] + dp[i - 2].
While deriving dp[i], always remember the definition of dp[i] to prevent divergence.
This highlights the importance of determining the meaning of the dp array and its indices.
- Initialize the dp array.
Review the definition of dp[i]: There are dp[i] ways to climb to the i-th step.
For i = 0, what should dp[i] be? There can be many explanations, but commonly it's directly rationalized for the answer.
For instance, one explanation might be that there is one way to ‘climb’ to the zeroth step, which is to do nothing, hence dp[0] = 1, as if you’re already at the top.
However, I think the more straightforward context is to consider the fact you're starting at the top: dp[0] = 0 because if you're already on the ground, there's no climbing involved.
In reality, such arguments are often moot because explaining dp[0] = 1 is typically due to it working in the recursive process where i starts at 2, allowing the problem to solve over itself, then rationalizing backward for the result.
From the perspective of the dp array definition, dp[0] = 0 is equally valid.
Notice: The problem states n is a positive integer, which implies n is not meant to be 0.
Thus, initialization for dp[0] is essentially irrelevant for this problem!
I believe most will concur that dp[1] = 1 and dp[2] = 2 are straightforward initializations.
Therefore, my principle is: without concern for dp[0], directly initialize dp[1] = 1, dp[2] = 2, and start recursion from i = 3, aligning with dp[i] definitions.
- Determine the traversal order.
From the recurrence formula dp[i] = dp[i - 1] + dp[i - 2];, it's clear the traversal order should be forward.
- Exemplify and derive the dp array.
Let's examine an example where n is 5:
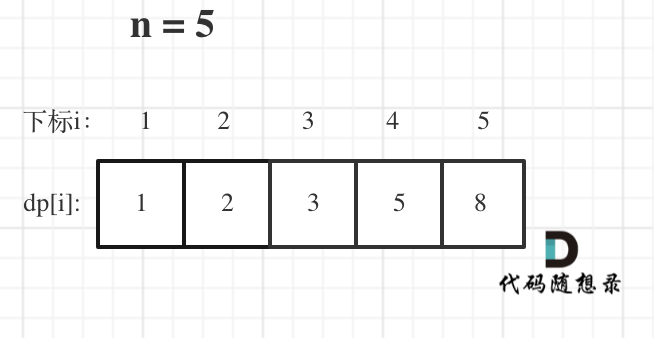
If there is an issue in the code, print out the dp table to see if it aligns with your expectations.
You might notice now that this is essentially the Fibonacci sequence!
The only difference is there's no need to consider how to initialize dp[0], as it holds no meaning for this problem!
After analyzing the five steps, the C++ code is as follows:
// Version 1
class Solution {
public:
int climbStairs(int n) {
if (n <= 1) return n; // To prevent null pointers, as dp[2] is directly referenced.
vector<int> dp(n + 1);
dp[1] = 1;
dp[2] = 2;
for (int i = 3; i <= n; i++) { // Notice that i starts from 3
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
- Time complexity: O(n)
- Space complexity: O(n)
Of course, space optimization is possible, as in the following code:
// Version 2
class Solution {
public:
int climbStairs(int n) {
if (n <= 1) return n;
int dp[3];
dp[1] = 1;
dp[2] = 2;
for (int i = 3; i <= n; i++) {
int sum = dp[1] + dp[2];
dp[1] = dp[2];
dp[2] = sum;
}
return dp[2];
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
- Time complexity: O(n)
- Space complexity: O(1)
In subsequent content dealing with dynamic programming, many problems also rely on previous two or three states to facilitate space optimization. However, I believe writing Version 1 in an interview is usually sufficient—clear and understandable. Further optimization might be pursued if requested by the interviewer.
Version 1 truly showcases the core ideas of dynamic programming and state transition.
# Expansion
This problem can be extended further: In addition to 1 or 2 steps at a time, what if you could climb up to m steps? How many ways to reach the top?
This takes the problem to a new level of complexity, essentially becoming a complete knapsack problem, though no direct problem exists on LeetCode for this, you can practice it on Kamacoder: 57. Climbing Stairs (opens new window)
Later, in discussions about knapsack problems, this problem will be revisited from a knapsack perspective. For an early insight, refer to the article: 70. Climbing Stairs Complete Knapsack Version (opens new window)
Here's the code for this variation:
class Solution {
public:
int climbStairs(int n) {
vector<int> dp(n + 1, 0);
dp[0] = 1;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) { // Change m to 2 to match the original climb stairs problem
if (i - j >= 0) dp[i] += dp[i - j];
}
}
return dp[n];
}
};
2
3
4
5
6
7
8
9
10
11
12
13
In the code above, m represents the maximum steps you can climb.
Note: The code above can’t be executed directly. It mainly illustrates that replacing m with 2 in the original case can solve the climbing stairs problem. Try it if you’re curious!.
You might observe that this could be an excellent problem for tech company interviews, where the first problem is the straightforward climbing stairs task. If the candidate defines dp[0] as 1, the conversation can delve into why dp[0] is initialized as 1, prompting the candidate to find various reasons to justify their approach. Here lies a critical evaluation point of the deeper understanding of dp[i]'s definition.
Subsequently, if the question extends to asking how one might climb if each step could involve up to m steps, it evolves into a more sophisticated challenge not directly available on LeetCode, serving as a superb test of algorithmic prowess.
After executing this sequence of questions, the candidate's algorithmic knowledge should be gauged well by the interviewer's perspective.
Notably, major tech corporations often favor delving deep into seemingly straightforward problems, subtly transformed to probe the candidate's comprehension and problem-solving abilities.
# Summary
This problem shares much in common with the "0509. Fibonacci Number" problem (opens new window), yet exhibits more complexity compared to it. The "0509. Fibonacci Number" (opens new window) problem description virtually provides the recursive formula and initialization details, and other elements emerge naturally.
However, this problem requires step-by-step analysis. Perhaps now, you might appreciate the "Dynamic Programming Fundamentals" five-step approach illuminating the Fibonacci problem's simplicity in applying the methodology.
Simple problems excel as vehicles for grasping methodologies. Awash with intuitive solutions one might breeze through, possessing the capability to encapsulate methods and articulate them brings the necessary proficiencies to master them efficiently and elegantly!
# Other Language Versions
# Java
// Regular method
public int climbStairs(int n) {
int[] dp = new int[n + 1];
dp[0] = 1;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
2
3
4
5
6
7
8
9
10
// Using variables instead of an array
class Solution {
public int climbStairs(int n) {
if(n <= 2) return n;
int a = 1, b = 2, sum = 0;
for(int i = 3; i <= n; i++){
sum = a + b; // f(i - 1) + f(i - 2)
a = b; // Update f(i - 1), used as f(i - 2) in next round
b = sum; // Update f(i), used as f(i - 1) in next round
}
return b;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
# Python
Dynamic Programming (Version One)
# Space complexity O(n)
class Solution:
def climbStairs(self, n: int) -> int:
if n <= 1:
return n
dp = [0] * (n + 1)
dp[1] = 1
dp[2] = 2
for i in range(3, n + 1):
dp[i] = dp[i - 1] + dp[i - 2]
return dp[n]
2
3
4
5
6
7
8
9
10
11
12
13
14
Dynamic Programming (Version Two)
# Space complexity O(3)
class Solution:
def climbStairs(self, n: int) -> int:
if n <= 1:
return n
dp = [0] * 3
dp[1] = 1
dp[2] = 2
for i in range(3, n + 1):
total = dp[1] + dp[2]
dp[1] = dp[2]
dp[2] = total
return dp[2]
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Dynamic Programming (Version Three)
# Space complexity O(1)
class Solution:
def climbStairs(self, n: int) -> int:
if n <= 1:
return n
prev1 = 1
prev2 = 2
for i in range(3, n + 1):
total = prev1 + prev2
prev1 = prev2
prev2 = total
return prev2
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# Go
func climbStairs(n int) int {
if n == 1 {
return 1
}
dp := make([]int, n+1)
dp[1] = 1
dp[2] = 2
for i := 3; i <= n; i++ {
dp[i] = dp[i-1] + dp[i-2]
}
return dp[n]
}
2
3
4
5
6
7
8
9
10
11
12
# JavaScript
var climbStairs = function(n) {
// dp[i] indicates the number of ways to reach the i-th step
// dp[i] = dp[i - 1] + dp[i - 2]
let dp = [1, 2]
for(let i = 2; i < n; i++) {
dp[i] = dp[i - 1] + dp[i - 2]
}
return dp[n - 1]
};
2
3
4
5
6
7
8
9
# TypeScript
Climbing 2 steps
function climbStairs(n: number): number {
/**
dp[i]: Number of ways to reach the i-th step
dp[1]: 1;
dp[2]: 2;
...
dp[i]: dp[i - 1] + dp[i - 2];
*/
const dp: number[] = [];
dp[1] = 1;
dp[2] = 2;
for (let i = 3; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Climbing m steps
function climbStairs(n: number): number {
/**
Climb a maximum of m steps at a time
dp[i]: Number of ways to reach the i-th step
dp[1]: 1;
dp[2]: 2;
dp[3]: dp[2] + dp[1];
...
dp[i]: dp[i - 1] + dp[i - 2] + ... + dp[max(i - m, 1)]; adding from i-1 to max(i-m, 1)
*/
const m: number = 2; // For this problem, m is 2
const dp: number[] = new Array(n + 1).fill(0);
dp[1] = 1;
dp[2] = 2;
for (let i = 3; i <= n; i++) {
const end: number = Math.max(i - m, 1);
for (let j = i - 1; j >= end; j--) {
dp[i] += dp[j];
}
}
return dp[n];
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# C
int climbStairs(int n){
// If n <= 2, return n
if(n <= 2)
return n;
// Initialize dp array with size n+1
int *dp = (int *)malloc(sizeof(int) * (n + 1));
dp[0] = 0, dp[1] = 1, dp[2] = 2;
// Traverse the array from the front, dp[i] = dp[i-1] + dp[i-2]
int i;
for(i = 3; i <= n; ++i) {
dp[i] = dp[i - 1] + dp[i - 2];
}
// Return dp[n]
return dp[n];
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Optimize Space Complexity:
int climbStairs(int n){
// If n <= 2, return n
if(n <= 2)
return n;
// Initialize dp array with size 3
int *dp = (int *)malloc(sizeof(int) * 3);
dp[1] = 1, dp[2] = 2;
// Only keep track of the states of the previous two steps
int i;
for(i = 3; i <= n; ++i) {
int sum = dp[1] + dp[2];
dp[1] = dp[2];
dp[2] = sum;
}
// Return dp[2]
return dp[2];
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# Scala
object Solution {
def climbStairs(n: Int): Int = {
if (n <= 2) return n
var dp = new Array[Int](n + 1)
dp(1) = 1
dp(2) = 2
for (i <- 3 to n) {
dp(i) = dp(i - 1) + dp(i - 2)
}
dp(n)
}
}
2
3
4
5
6
7
8
9
10
11
12
Optimize Space Complexity:
object Solution {
def climbStairs(n: Int): Int = {
if (n <= 2) return n
var (a, b) = (1, 2)
for (i <- 3 to n) {
var tmp = a + b
a = b
b = tmp
}
b // Finally return b
}
}
2
3
4
5
6
7
8
9
10
11
12
# C#
public class Solution {
public int ClimbStairs(int n) {
if(n<=2) return n;
int[] dp = new int[2] { 1, 2 };
for (int i = 3; i <= n; i++)
{
int temp = dp[0] + dp[1];
dp[0] = dp[1];
dp[1] = temp;
}
return dp[1];
}
}
2
3
4
5
6
7
8
9
10
11
12
13
# Rust
impl Solution {
pub fn climb_stairs(n: i32) -> i32 {
if n <= 1 {
return n;
}
let (mut a, mut b, mut f) = (1, 1, 0);
for _ in 2..=n {
f = a + b;
a = b;
b = f;
}
f
}
2
3
4
5
6
7
8
9
10
11
12
13
Using a dp array:
impl Solution {
pub fn climb_stairs(n: i32) -> i32 {
let n = n as usize;
let mut dp = vec![0; n + 1];
dp[0] = 1;
dp[1] = 1;
for i in 2..=n {
dp[i] = dp[i - 1] + dp[i - 2];
}
dp[n]
}
}
2
3
4
5
6
7
8
9
10
11
12
