# 309. Best Time to Buy and Sell Stock with Cooldown
LeetCode Problem Link (opens new window)
Given an integer array, where the i-th element represents the stock price on day i.
Design an algorithm to calculate the maximum profit. You may complete as many transactions as you like (multiple buys and sells of one stock) under the following constraints:
- You cannot engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
- After selling your stock, you cannot buy stock on the next day (i.e., cooldown period of 1 day).
Example:
- Input: [1,2,3,0,2]
- Output: 3
- Explanation: Transactions are: [buy, sell, cooldown, buy, sell]
# Thought Process
Compared to 0122.Best Time to Buy and Sell Stock II (Dynamic Programming) (opens new window), this problem adds a cooldown period.
In 0122.Best Time to Buy and Sell Stock II (Dynamic Programming) (opens new window), there are two states: maximum cash after holding the stock and maximum cash after not holding the stock.
Dynamic programming five steps, analysis as follows:
- Define the dp array and the meaning of the index
dp[i][j]: Maximum cash on the i-th day with the j-th state.
The complexity for many learners arises due to the introduction of the cooldown period, which adds complexity to the states, such as buying today, selling today, being in a cooldown period today, all of which represent not being able to operate stock.
Specifically, it can be divided into the following four states:
- State 1: Holding stock (either bought today or held from a previous buy without any operation)
- Not holding stock, which includes two states of selling stock
- State 2: Holding state of having sold stock (sold stock two days ago, went through one day of cooldown, or maintaining a state of having sold with no operations)
- State 3: Sold stock today
- State 4: Cooldown period today, but a cooldown state is non-persistent and lasts only one day!
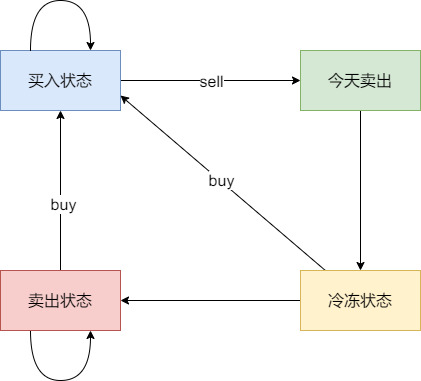
The state of j is:
- 0: State 1
- 1: State 2
- 2: State 3
- 3: State 4
The reason why many explanations are vague is that these four states are merged into three states, specifically merging State 2 and State 4.
From a coding perspective, it indeed can be merged, but logically after merging it becomes very difficult to understand, so my explanation below is based on these four states, analyzing each state clearly.
If you follow the order of the Keet Coder, you’ll notice that in the Best Time to Buy and Sell Stock series of explanations,
- 0121.Best Time to Buy and Sell Stock (opens new window)
- 0122.Best Time to Buy and Sell Stock II (Dynamic Programming) (opens new window)
- 0123.Best Time to Buy and Sell Stock III (opens new window)
- 0188.Best Time to Buy and Sell Stock IV (opens new window)
I have not introduced a separate state for selling stock today, categorizing it as not holding stock state. But in this problem, why list selling stock today as a separate state?
Because, with a cooldown period, the day before a cooldown period can only be the state of selling stock today. If it is not holding stock state, then it becomes unclear as it may not involve a selling operation.
If you haven’t brushed up on the Keet Coder chapters before this, you might be a bit puzzled here. I suggest reviewing the explanations of stock content before this in Keet Coder, to grasp the settings for each day’s state.
Note that each of these states, such as State 1 (holding stock), does not mean you must buy stock today, but rather maintain the state of having bought stock, i.e., you may have bought it a few days ago and then performed no operations, hence maintaining the bought state.
- Determining the recursive formula
To achieve the holding stock state (State 1), i.e., dp[i][0], there are two specific actions:
- Action 1: Carrying forward the holding stock state (State 1) from the previous day, dp[i][0] = dp[i - 1][0]
- Action 2: Buying today, with two possibilities
- Previous day was a cooldown (State 4), dp[i - 1][3] - prices[i]
- Previous day was maintaining sold stock state (State 2), dp[i - 1][1] - prices[i]
Thus, dp[i][0] = max(dp[i - 1][0], dp[i - 1][3] - prices[i], dp[i - 1][1] - prices[i]);
To achieve the holding sold stock state (State 2), i.e., dp[i][1], two specific actions:
- Action 1: Previous day was already State 2
- Action 2: Previous day was a cooldown (State 4)
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
To achieve selling stock today state (State 3), i.e., dp[i][2], only one specific action:
Yesterday must have been holding stock state (State 1), sell today
i.e., dp[i][2] = dp[i - 1][0] + prices[i];
To achieve cooldown state (State 4), i.e., dp[i][3], only one specific action:
Yesterday had been selling stock (State 3)
dp[i][3] = dp[i - 1][2];
From above analysis, the recursive formula code is as follows:
dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3], dp[i - 1][1]) - prices[i]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
dp[i][2] = dp[i - 1][0] + prices[i];
dp[i][3] = dp[i - 1][2];
2
3
4
- How to initialize the dp array
This mainly discusses how to initialize on day 0.
If in holding stock state (State 1), then: dp[0][0] = -prices[0], meaning the stock must be bought on that day.
For maintaining sold stock state (State 2), it’s hard to clearly define an initial value from the definition of State 2, in such situations we refer to what the recursive formula needs it to initialize to.
Assuming i is 1, stock bought on day 1, the recursive formula involves calculating dp[i - 1][1] - prices[i], i.e., dp[0][1] - prices[1]. Now, feel what dp[0][1] (State 2 of day 0) should initialize to: it must be initialized to 0. Imagine it initialized to any other value. The cash remaining after buying stock on day 1 would not match the reality.
Selling stock today (State 3), as per above analysis, dp[0][2] initializes to 0, so does dp[0][3].
- Determine the order of traversal
The recursive formula shows dp[i] relies on dp[i-1], thus traversing from front to back.
- Example of deriving dp array
Take [1,2,3,0,2] as an example, the dp array is:
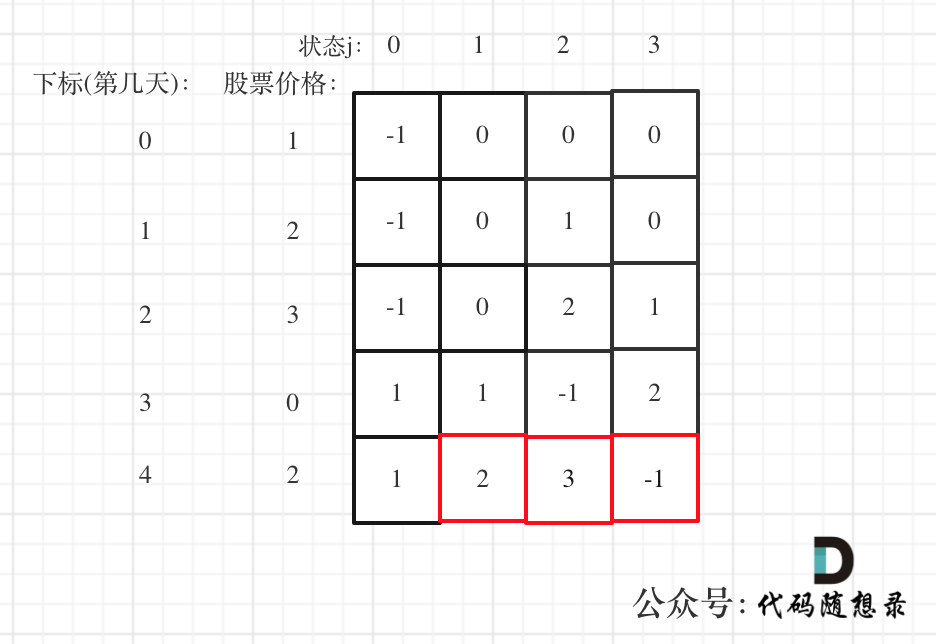
At last, fetching the max value from State 2, State 3, and State 4 gives you the result. Forgetting the cooldown state is common, but the cooldown state is crucial as on the last day it might be the largest.
Below’s the code:
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
if (n == 0) return 0;
vector<vector<int>> dp(n, vector<int>(4, 0));
dp[0][0] -= prices[0]; // Hold stock
for (int i = 1; i < n; i++) {
dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3] - prices[i], dp[i - 1][1] - prices[i]));
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
dp[i][2] = dp[i - 1][0] + prices[i];
dp[i][3] = dp[i - 1][2];
}
return max(dp[n - 1][3], max(dp[n - 1][1], dp[n - 1][2]));
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
- Time Complexity: O(n)
- Space Complexity: O(n)
Of course, space complexity can be optimized to a dp[2][4] sized array, by only storing states of the previous and current day. Enthusiasts can try writing this, as the thought process remains the same.
# Conclusion
This time the problem with the cooldown period is explained in detail, divided into four states with clear state transitions. It is strongly recommended to analyze this using four states; a three-state division can easily lead to confusion.
# Other Language Versions
# Java:
class Solution {
public int maxProfit(int[] prices) {
if (prices == null || prices.length < 2) {
return 0;
}
int[][] dp = new int[prices.length][2];
// bad case
dp[0][0] = 0;
dp[0][1] = -prices[0];
dp[1][0] = Math.max(dp[0][0], dp[0][1] + prices[1]);
dp[1][1] = Math.max(dp[0][1], -prices[1]);
for (int i = 2; i < prices.length; i++) {
// dp formula
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 2][0] - prices[i]);
}
return dp[prices.length - 1][0];
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// using 2*4 array for space optimization
// Here is a brief mention, that when I submitted to LeetCode, the performance of the 2*4 2-D array is almost the same as the 1-D array performance below
// both are time: 1ms, space: 40.X MB (actually a length*4 2-D array is just space: 41.X MB, which doesn't seem like much)
// Stock-based DP problems are generally like this, just treat it as an extension. If someone really asks about optimization, you at least have something to talk about.
class Solution {
/**
1. [i][0] holding the stock
2. [i][1] after cooldown but still not buying the stock
3. [i][2] selling the stock
4. [i][3] cooldown
*/
public int maxProfit(int[] prices) {
int len = prices.length;
int dp[][] = new int [2][4];
dp[0][0] = -prices[0];
for(int i = 1; i < len; i++){
dp[i % 2][0] = Math.max(Math.max(dp[(i - 1) % 2][0], dp[(i - 1) % 2][1] - prices[i]), dp[(i - 1) % 2][3] - prices[i]);
dp[i % 2][1] = Math.max(dp[(i - 1) % 2][1], dp[(i - 1) % 2][3]);
dp[i % 2][2] = dp[(i - 1) % 2][0] + prices[i];
dp[i % 2][3] = dp[(i - 1) % 2][2];
}
return Math.max(Math.max(dp[(len - 1) % 2][1], dp[(len - 1) % 2][2]), dp[(len - 1) % 2][3]);
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
// One-dimensional array optimization
class Solution {
public int maxProfit(int[] prices) {
int[] dp=new int[4];
dp[0] = -prices[0];
dp[1] = 0;
for(int i = 1; i <= prices.length; i++){
// Use a temporary variable to store dp[0], dp[2]
// Because dp[0] and dp[2]'s data will soon change
int temp = dp[0];
int temp1 = dp[2];
dp[0] = Math.max(dp[0], Math.max(dp[3], dp[1]) - prices[i]);
dp[1] = Math.max(dp[1], dp[3]);
dp[2] = temp + prices[i];
dp[3] = temp1;
}
return Math.max(dp[3],Math.max(dp[1],dp[2]));
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// Alternate solution approach
class Solution {
public int maxProfit(int[] prices) {
int[][] dp = new int[prices.length + 1][2];
dp[1][0] = -prices[0];
for (int i = 2; i <= prices.length; i++) {
/*
dp[i][0] Max profit holding stocks on day i;
dp[i][1] Max profit not holding stocks on day i;
Situation one: today is a cooldown, can't buy stocks by dp[i-1][1], so buy by dp[i - 2][1], no issue
Situation two: today is not a cooldown, theoretically should buy by dp[i-1][1], but today's not-cooldown means stocks weren't sold yesterday,
So dp[i-1][1]=dp[i-2][1], thus buy using dp[i-2][1], no issue
*/
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 2][1] - prices[i - 1]);
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] + prices[i - 1]);
}
return dp[prices.length][1];
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# Python:
Version 1
from typing import List
class Solution:
def maxProfit(self, prices: List[int]) -> int:
n = len(prices)
if n == 0:
return 0
dp = [[0] * 4 for _ in range(n)] # Create a dynamic programming array, 4 states representing holding stocks, not holding stocks and being in a cooldown, not holding stocks and not being in a cooldown, and selling stocks that day resulting in cooldown
dp[0][0] = -prices[0] # Initial state: the maximum profit for holding stocks on the first day is the price of buying the stock
for i in range(1, n):
dp[i][0] = max(dp[i-1][0], max(dp[i-1][3] - prices[i], dp[i-1][1] - prices[i])) # The maximum profit for holding stocks today is the same as yesterday for holding stocks or not holding stocks and not being in cooldown from yesterday minus today's stock price
dp[i][1] = max(dp[i-1][1], dp[i-1][3]) # The maximum profit for not holding stocks and being in cooldown today is the same as yesterday for holding stocks plus today's stock price
dp[i][2] = dp[i-1][0] + prices[i] # The maximum profit for not holding stocks and not being in a cooldown is the same as yesterday for not holding stocks and today being sold
dp[i][3] = dp[i-1][2] # The maximum profit for being in cooldown is the same as yesterday for being in a not holding stock and not being in a cooldown
return max(dp[n-1][3], dp[n-1][1], dp[n-1][2]) # Return the maximum profit for not holding stocks on the last day
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Version 2
class Solution:
def maxProfit(self, prices: List[int]) -> int:
n = len(prices)
if n < 2:
return 0
# Define three states in the dynamic programming array
dp = [[0] * 3 for _ in range(n)]
dp[0][0] = -prices[0] # Maximum profit when holding stock
dp[0][1] = 0 # Maximum profit when not holding stock and in a cooldown period
dp[0][2] = 0 # Maximum profit when not holding stock and not in a cooldown period
for i in range(1, n):
# The maximum profit when holding stock today is equal to the maximum profit yesterday when holding stock, or the maximum profit from two days ago when not holding stock minus today's stock price
dp[i][0] = max(dp[i-1][0], dp[i-2][1] - prices[i])
# The maximum profit when not holding stock and in a cooldown period today is equal to yesterday's maximum profit when holding stock and selling it today
dp[i][1] = dp[i-1][0] + prices[i]
# The maximum profit when not holding stocks and not in a cooldown period today is equal to the maximum profit of not holding stocks yesterday, or it was in a cooldown period
dp[i][2] = max(dp[i-1][2], dp[i-1][1])
# Return the maximum profit for not holding stock on the last day
return max(dp[-1][1], dp[-1][2])
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Version 3
class Solution:
def maxProfit(self, prices: List[int]) -> int:
# 0: holding stocks
# (1) keep holding stocks: dp[i][0] = dp[i - 1][0]
# (2) buy stocks: dp[i][0] = dp[i - 1][1] - price, or dp[i - 1][3] - price
# 1: keep no stocks: dp[i][1] = dp[i - 1][1]
# 2: sell stocks: dp[i][2] = dp[i - 1][0] + price
# 3: cooldown day: dp[i][3] = dp[i - 1][2]
dp = [-prices[0], 0, 0, 0]
for price in prices[1:]:
dc = dp.copy() # This is key, keep the state from the previous day, don’t overwrite, only use it later, making the logic simple and easy to understand
dp[0] = max(
dc[0],
dc[1] - price,
dc[3] - price
)
dp[1] = max(
dc[1],
dc[3]
)
dp[2] = dc[0] + price
dp[3] = dc[2]
return max(dp)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# Go:
// Best Time to Buy and Sell Stock with Cooldown Dynamic Programming
// Time Complexity O(n) Space Complexity O(n)
func maxProfit(prices []int) int {
n := len(prices)
if n < 2 {
return 0
}
dp := make([][]int, n)
status := make([]int, n * 4)
for i := range dp {
dp[i] = status[:4]
status = status[4:]
}
dp[0][0] = -prices[0]
for i := 1; i < n; i++ {
dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][1] - prices[i], dp[i - 1][3] - prices[i]))
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3])
dp[i][2] = dp[i - 1][0] + prices[i]
dp[i][3] = dp[i - 1][2]
}
return max(dp[n - 1][1], max(dp[n - 1][2], dp[n - 1][3]))
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
// One-dimensional optimization version
// Time Complexity O(n), Space Complexity O(1)
func maxProfit(prices []int) int {
// 0: Hold stock, either keep holding or buy stock
// 1: No stock, keep the state of not holding (ignoring previous day sell, as that's cooldown, with a state distinction)
// 2: No stock, sell today
// 3: Cooldown, the previous day sold
dp0, dp1, dp2, dp3 := -prices[0], 0, 0, 0
n := len(prices)
for i := 1; i < n; i++ {
t0 := max(dp0, max(dp1, dp3) - prices[i])
t1 := max(dp1, dp3)
t2 := dp0 + prices[i]
t3 := dp2
// Update
dp0, dp1, dp2, dp3 = t0, t1, t2, t3
}
return max(dp1, max(dp2, dp3))
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# JavaScript:
Different state definitions that seem easier to understand
function maxProfit(prices) {
// State of day i hold sell not cool(no stock) the cooldown
const dp = new Array(prices.length).fill(0).map(() => [0, 0, 0, 0]);
dp[0][0] = -prices[0];
for (let i = 1; i < prices.length; i++) {
// Hold
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][2] - prices[i]);
// Sell
dp[i][1] = dp[i - 1][0] + prices[i];
// Not in cooldown
dp[i][2] = Math.max(dp[i - 1][2], dp[i - 1][1]);
// Cooldown (sold the previous day)
dp[i][3] = dp[i - 1][1];
}
return Math.max(...dp.pop());
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
const maxProfit = (prices) => {
if(prices.length < 2) {
return 0
} else if(prices.length < 3) {
return Math.max(0, prices[1] - prices[0]);
}
let dp = Array.from(Array(prices.length), () => Array(4).fill(0));
dp[0][0] = 0 - prices[0];
for(i = 1; i < prices.length; i++) {
dp[i][0] = Math.max(dp[i - 1][0], Math.max(dp[i-1][1], dp[i-1][3]) - prices[i]);
dp[i][1] = Math.max(dp[i -1][1], dp[i - 1][3]);
dp[i][2] = dp[i-1][0] + prices[i];
dp[i][3] = dp[i-1][2];
}
return Math.max(dp[prices.length - 1][1], dp[prices.length - 1][2], dp[prices.length - 1][3]);
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// Space Optimization with One-dimensional array
const maxProfit = (prices) => {
const n = prices.length
const dp = new Array(4).fill(0)
dp[0] = -prices[0]
for (let i = 1; i < n; i ++) {
const temp = dp[0] // Cache the previous state
const temp1 = dp[2]
dp[0] = Math.max(dp[0], Math.max(dp[3] - prices[i], dp[1] - prices[i])) // Hold
dp[1] = Math.max(dp[1], dp[3]) // Not holding, not bought
dp[2] = temp + prices[i] // Sell today
dp[3] = temp1 // Cooldown
}
return Math.max(...dp)
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# TypeScript:
Version 1 consistent with the thought process in this article
function maxProfit(prices: number[]): number {
/**
dp[i][0]: Holding stock;
dp[i][1]: No stock, not in cooldown;
dp[i][2]: Sold today;
dp[i][3]: Cooldown period;
*/
const length: number = prices.length;
const dp: number[][] = new Array(length).fill(0).map(_ => []);
dp[0][0] = -prices[0];
dp[0][1] = dp[0][2] = dp[0][3] = 0;
for (let i = 1; i < length; i++) {
dp[i][0] = Math.max(
dp[i - 1][0],
Math.max(dp[i - 1][3] - prices[i], dp[i - 1][1] - prices[i])
);
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][3]);
dp[i][2] = dp[i - 1][0] + prices[i];
dp[i][3] = dp[i - 1][2];
}
const lastEl: number[] = dp[length - 1];
return Math.max(lastEl[1], lastEl[2], lastEl[3]);
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Version 2, with slightly different state definitions for understanding
function maxProfit(prices: number[]): number {
/**
dp[i][0]: Holding stock, bought today;
dp[i][1]: Holding stock, not bought today;
dp[i][2]: No stock, sold today;
dp[i][3]: No stock, not sold today;
Buying has a cooldown restriction, which means dp[0] can only come from the state of the previous day dp[3];
If there’s a cooldown restriction on selling, that means dp[2] comes from dp[1].
*/
const length: number = prices.length;
const dp: number[][] = new Array(length).fill(0).map(_ => []);
dp[0][0] = -prices[0];
dp[0][1] = -Infinity;
dp[0][2] = dp[0][3] = 0;
for (let i = 1; i < length; i++) {
dp[i][0] = dp[i - 1][3] - prices[i];
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0]);
dp[i][2] = Math.max(dp[i - 1][0], dp[i - 1][1]) + prices[i];
dp[i][3] = Math.max(dp[i - 1][3], dp[i - 1][2]);
}
return Math.max(dp[length - 1][2], dp[length - 1][3]);
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# C:
#define max(a, b) ((a) > (b) ? (a) : (b))
/**
* State 1: Holding stock (today bought stock,
* orheld from previous buy without operation)
* Not holding stock states, with two sold stock states:
* State 2: Holding sold stock state (sold stock two days ago, underwent a day of cooldown,
* or maintaining sold state without operations)
* State 3: Sold stock today
* State 4: Cooldown today, but cooldown cannot persist, lasts one day only!
*/
int maxProfit(int* prices, int pricesSize) {
if(pricesSize == 0){
return 0;
}
int dp[pricesSize][4];
memset(dp, 0, sizeof (int ) * pricesSize * 4);
dp[0][0] = -prices[0];
for (int i = 1; i < pricesSize; ++i) {
dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][1] - prices[i], dp[i - 1][3] - prices[i]));
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
dp[i][2] = dp[i - 1][0] + prices[i];
dp[i][3] = dp[i - 1][2];
}
return max(dp[pricesSize - 1][1], max(dp[pricesSize - 1][2], dp[pricesSize - 1][3]));
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# Rust:
impl Solution {
pub fn max_profit(prices: Vec<i32>) -> i32 {
/*
* dp[i][0]: Holding stock state;
* dp[i][1]: No stock state, not being in cooldown;
* dp[i][2]: No stock state, sold today;
* dp[i][3]: No stock state, being in cooldown;
*/
let mut dp = vec![vec![0; 4]; prices.len()];
dp[0][0] = -prices[0];
for (i, &p) in prices.iter().enumerate().skip(1) {
dp[i][0] = dp[i - 1][0].max((dp[i - 1][1] - p).max(dp[i - 1][3] - p));
dp[i][1] = dp[i - 1][1].max(dp[i - 1][3]);
dp[i][2] = dp[i - 1][0] + p;
dp[i][3] = dp[i - 1][2];
}
*dp[prices.len() - 1].iter().skip(1).max().unwrap()
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
