392. Is Subsequence

LeetCode Problem Link (opens new window)

Given strings s and t, determine if s is a subsequence of t.

A subsequence of a string is a new string formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (For example, "ace" is a subsequence of "abcde" while "aec" is not).

Example 1:

• Input: s = "abc", t = "ahbgdc"
• Output: true

Example 2:

• Input: s = "axc", t = "ahbgdc"
• Output: false

Constraints:

• 0 <= s.length <= 100
• 0 <= t.length <= 10^4

Both strings consist only of lowercase characters.

Approach

(This problem can also be solved using the two-pointer approach with a time complexity of O(n))

This problem can be considered an introductory problem to edit distance, as we only need to calculate deletions in this case and do not need to consider insertions or replacements.

Mastering the dynamic programming approach for this problem lays the foundation for more advanced edit distance problems.

Here is an analysis using the five-step dynamic programming approach:

1. Define the dp array and the meaning of its indices

dp[i][j] indicates the length of the longest common subsequence for the string s ending at i-1 and the string t ending at j-1.

Note that we are checking if s is a subsequence of t, meaning t's length is greater than or equal to s.

You might be wondering why use i-1 to represent the ending index of the string. Why not i?

The reason for this definition is explained in detail in 0718.Maximum Length of Repeated Subarray (opens new window).

Using i as the representation is also possible!

However, by consistently representing it as the string ending at i-1, the subsequent recursive formulas become easier to understand, as explained further below.

2. Define the recursive formula

When determining the recursive formula, consider the following two operations:

• if (s[i - 1] == t[j - 1])
  • Found a character in t that also appears in s
• if (s[i - 1] != t[j - 1])
  • Equivalent to removing an element from t, continue matching

If (s[i - 1] == t[j - 1]), then dp[i][j] = dp[i - 1][j - 1] + 1; because you've found a common character, the length of the common subsequence naturally increases by 1 based on dp[i-1][j-1] (if unclear, review the definition of dp[i][j]).

If (s[i - 1] != t[j - 1]), it is equivalent to removing the element from t, and then dp[i][j] is based on the matching result of s[i - 1] and t[j - 2], namely: dp[i][j] = dp[i][j - 1].

You can see that this recursive formula is essentially the same as that for the 1143.Longest Common Subsequence (opens new window), with the distinction being that in this problem, when removing elements it is always from string t, whereas in 1143 both strings can have elements removed.

3. How to initialize the dp array

From the recursive formula, it's clear that both dp[i][j] depend on dp[i - 1][j - 1] and dp[i][j - 1], hence dp[0][0] and dp[i][0] must be initialized.

Here, you can see why when defining dp[i][j] it was crucial to state it represents the string s ending at i-1 and the string t ending at j-1, forming the longest common subsequence of length dp[i][j].

Because such a definition in the dp matrix leaves space for initialization, as illustrated:

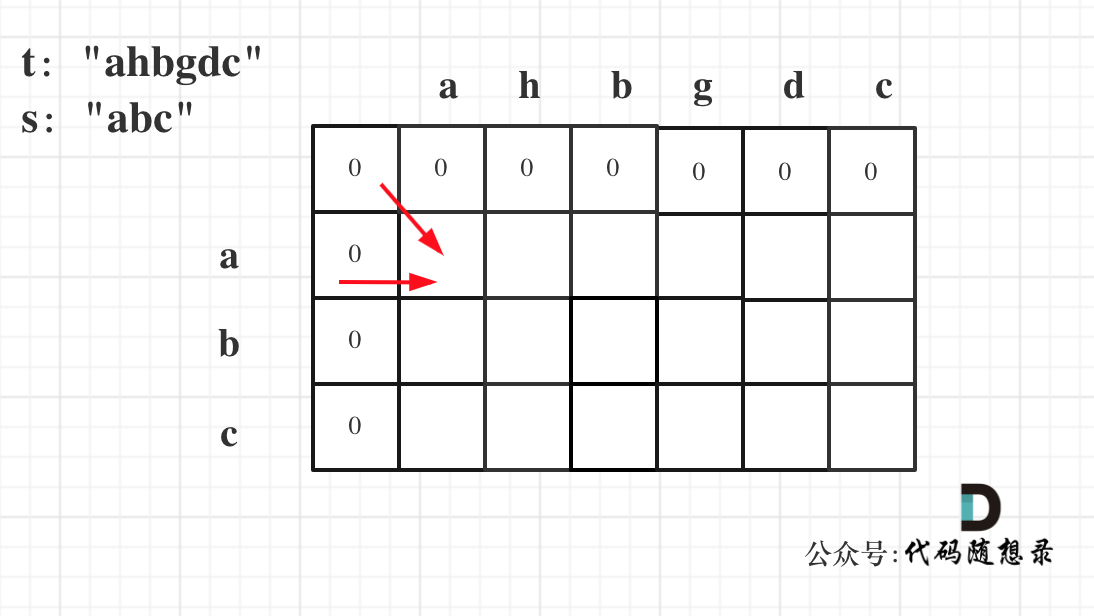
If you had defined dp[i][j] as ending at i and ending at j, initialization would be more cumbersome.

dp[i][0] represents the length of the common subsequence of the string ending at i-1 with an empty string, hence 0. The same applies to dp[0][j].

vector<vector<int>> dp(s.size() + 1, vector<int>(t.size() + 1, 0));

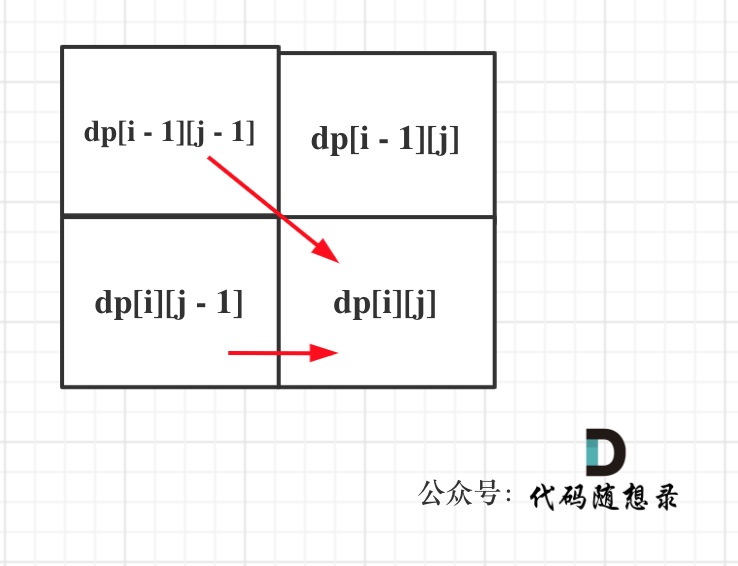
4. Determine the order of traversal

Similarly, from the recursive formula, it's clear that both dp[i][j] depend on dp[i - 1][j - 1] and dp[i][j - 1], and thus traversal should progress from top to bottom and left to right.

Illustrated as follows:

5. Example walkthrough of the dp array

Take example 1: Input: s = "abc", t = "ahbgdc". The dp state transition diagram is as follows:

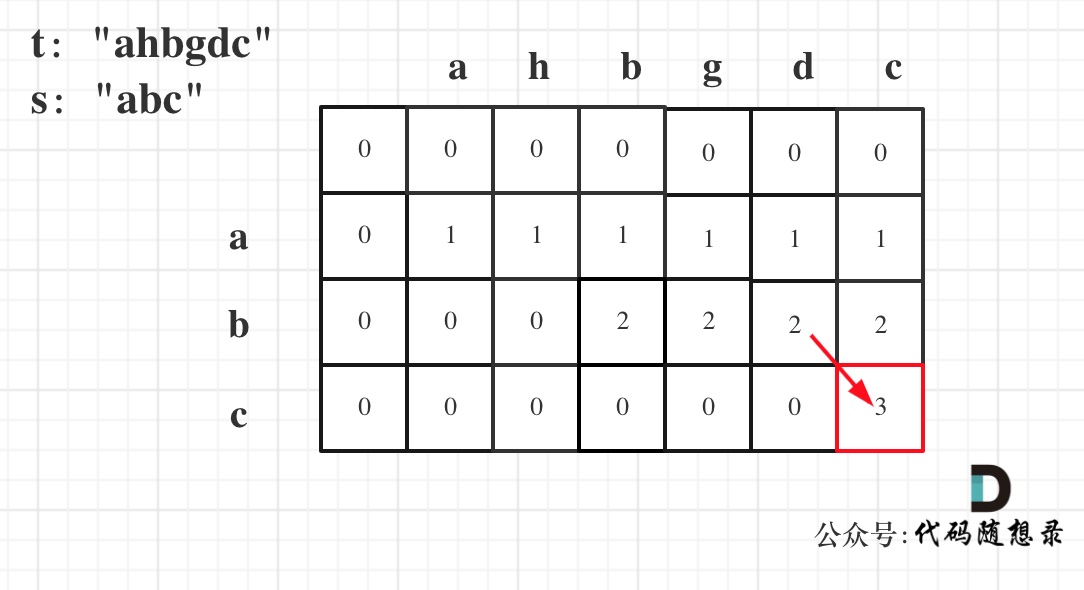
dp[i][j] represents the length of the longest common subsequence of the string s ending at i-1 and the string t ending at j-1, so if dp[s.size()][t.size()] equals the length of string s, it indicates that the longest common subsequence of s and t is s, therefore s is a subsequence of t.

In the diagram dp[s.size()][t.size()] = 3, while s.size() is also 3. So, s is a subsequence of t, and return true.

The five-step dynamic programming analysis concludes here and here is the C++ code:

class Solution {
public:
    bool isSubsequence(string s, string t) {
        vector<vector<int>> dp(s.size() + 1, vector<int>(t.size() + 1, 0));
        for (int i = 1; i <= s.size(); i++) {
            for (int j = 1; j <= t.size(); j++) {
                if (s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
                else dp[i][j] = dp[i][j - 1];
            }
        }
        if (dp[s.size()][t.size()] == s.size()) return true;
        return false;
    }
};

• Time Complexity: O(n × m)
• Space Complexity: O(n × m)

Summary

This problem can be considered an introductory problem to edit distance problems (as it only involves subtraction) and is a classic example of dynamic programming solutions.

Such problems often appear complex when initially read and might seem even more so when simulated. But once the dynamic programming analysis is complete, the resulting code is brief.

In the previous problem explanations, we've discussed 1143.Longest Common Subsequence (opens new window), and you'll notice the similarities between this problem and 1143.

Edit distance problems best showcase the essence and cleverness of dynamic programming. It's worth thoroughly understanding them.

Other Language Versions

Java:

class Solution {
    public boolean isSubsequence(String s, String t) {
        int length1 = s.length(); int length2 = t.length();
        int[][] dp = new int[length1+1][length2+1];
        for(int i = 1; i <= length1; i++){
            for(int j = 1; j <= length2; j++){
                if(s.charAt(i-1) == t.charAt(j-1)){
                    dp[i][j] = dp[i-1][j-1] + 1;
                }else{
                    dp[i][j] = dp[i][j-1];
                }
            }
        }
        if(dp[length1][length2] == length1){
            return true;
        }else{
            return false;
        }
    }
}

After modifying the traversal order, the dp array can be compressed by using a rolling array.

class Solution {
    public boolean isSubsequence(String s, String t) {
        // Modify traversal order, traverse t in the outer loop and s in the inner loop. This results in dp relying only on the element directly above and the top-left diagonal element, making compression feasible.
        int[][] dp = new int[t.length() + 1][s.length() + 1];
        for (int i = 1; i < dp.length; i++) { // Traverse string t
            for (int j = 1; j < dp[i].length; j++) { // Traverse string s
                if (t.charAt(i - 1) == s.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = dp[i - 1][j];
                }
            }
            System.out.println(Arrays.toString(dp[i]));
        }
        return dp[t.length()][s.length()] == s.length();
    }
}

State Compression

class Solution {
    public boolean isSubsequence(String s, String t) {
        int[] dp = new int[s.length() + 1];
        for (int i = 0; i < t.length(); i ++) {
            // Need to use the previous iteration's dp[j - 1], so iterate in reverse
            for (int j = dp.length - 1; j > 0; j --) {
                // i iterates through string t, j iterates through the dp array, and the length of dp is one greater than that of s, thus the -1.
                if (t.charAt(i) == s.charAt(j - 1)) {
                    dp[j] = dp[j - 1] + 1;
                }
            }
        }
        return dp[s.length()] == s.length();
    }
}

Define dp as a boolean type; dp[i] directly represents whether s.substring(0, i) is a subsequence of t.

class Solution { 
    public boolean isSubsequence(String s, String t) {
        boolean[] dp = new boolean[s.length() + 1];
        // Represents "" as a subsequence of t
        dp[0] = true;
        for (int i = 0; i < t.length(); i ++) {
            for (int j = dp.length - 1; j > 0; j --) {
                if (t.charAt(i) == s.charAt(j - 1)) {
                    dp[j] = dp[j - 1];
                }
            }
        }
        return dp[dp.length - 1];
    }
}

Python：

class Solution:
    def isSubsequence(self, s: str, t: str) -> bool:
        dp = [[0] * (len(t)+1) for _ in range(len(s)+1)]
        for i in range(1, len(s)+1):
            for j in range(1, len(t)+1):
                if s[i-1] == t[j-1]:
                    dp[i][j] = dp[i-1][j-1] + 1
                else:
                    dp[i][j] = dp[i][j-1]
        if dp[-1][-1] == len(s):
            return True
        return False

JavaScript：

const isSubsequence = (s, t) => {
    // lengths of s and t
    const [m, n] = [s.length, t.length];
    // initialize dp with all zeros
    const dp = new Array(m + 1).fill(0).map(x => new Array(n + 1).fill(0));
    for (let i = 1; i <= m; i++) {
        for (let j = 1; j <= n; j++) {
            // update dp[i][j], two cases
            if (s[i - 1] === t[j - 1]) {
                dp[i][j] = dp[i - 1][j - 1] + 1;
            } else {
                dp[i][j] = dp[i][j - 1];
            }
        }
    }
    // after traversing, check if dp at bottom-right equals the length of s
    return dp[m][n] === m ? true : false;
};

TypeScript：

2-D Array

function isSubsequence(s: string, t: string): boolean {
    /**
        dp[i][j]: the length of the longest common subsequence for the first i-1 characters of s and the first j-1 characters of t
     */
    const sLen = s.length
    const tLen = t.length
    const dp: number[][] = new Array(sLen + 1).fill(0).map(_ => new Array(tLen + 1).fill(0))

    for (let i = 1; i <= sLen; i++) {
        for (let j = 1; j <= tLen; j++) {
            if (s[i - 1] === t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1
            // just take the dp value of j-2 without considering i-2
            else dp[i][j] = dp[i][j - 1]
        }
    }
    return dp[sLen][tLen] === s.length
}

Rolling Array

function isSubsequence(s: string, t: string): boolean {
    const sLen = s.length
    const tLen = t.length
    const dp: number[] = new Array(tLen + 1).fill(0)

    for (let i = 1; i <= sLen; i++) {
        let prev: number = 0;
        let temp: number = 0;
        for (let j = 1; j <= tLen; j++) {
            // Backup the current state (after the upper layer iteration)
            temp = dp[j]
            // prev is equivalent to dp[j-1] (accumulated with the upper layer state)
            if (s[i - 1] === t[j - 1]) dp[j] = prev + 1
            else dp[j] = dp[j - 1]
            // Continue using the previous layer state to update parameters for the current layer's next state
            prev = temp
        }
    }
    return dp[tLen] === sLen
}

Go:

2-D DP:

func isSubsequence(s string, t string) bool {
    dp := make([][]int, len(s) + 1)
    for i := 0; i < len(dp); i ++{
        dp[i] = make([]int, len(t) + 1)
    }
    for i := 1; i < len(dp); i ++{
        for j := 1; j < len(dp[i]); j ++{
            if s[i - 1] == t[j - 1] {
                dp[i][j] = dp[i - 1][j - 1] +1
            }else{
                dp[i][j] = dp[i][j - 1]
            }
        }
    }
    return dp[len(s)][len(t)] == len(s)
}

1-D DP:

func isSubsequence(s string, t string) bool {
    dp := make([]int, len(s) + 1)
    for i := 1; i <= len(t); i ++ {
        for j := len(s); j >= 1; j -- {
            if t[i - 1] == s[j - 1] {
                dp[j] = dp[j - 1] + 1
            }
        }
    }
    return dp[len(s)] == len(s)
}

Rust:

impl Solution {
    pub fn is_subsequence(s: String, t: String) -> bool {
        let mut dp = vec![vec![0; t.len() + 1]; s.len() + 1];
        for (i, char_s) in s.chars().enumerate() {
            for (j, char_t) in t.chars().enumerate() {
                if char_s == char_t {
                    dp[i + 1][j + 1] = dp[i][j] + 1;
                    continue;
                }
                dp[i + 1][j + 1] = dp[i + 1][j]
            }
        }
        dp[s.len()][t.len()] == s.len()
    }
}

Rolling Array

impl Solution {
    pub fn is_subsequence(s: String, t: String) -> bool {
        let mut dp = vec![0; t.len() + 1];
        let (s, t) = (s.as_bytes(), t.as_bytes());
        for &byte_s in s {
            let mut pre = 0;
            let mut temp = 0;
            for j in 0..t.len() {
                temp = dp[j + 1];
                if byte_s == t[j] {
                    dp[j + 1] = pre + 1;
                } else {
                    dp[j + 1] = dp[j];
                }
                pre = temp;
            }
        }
        dp[t.len()] == s.len()
    }
}