# 718. Maximum Length of Repeated Subarray
LeetCode Problem Link (opens new window)
Given two integer arrays A and B, return the maximum length of a subarray that appears in both arrays.
Example:
Input:
- A: [1,2,3,2,1]
- B: [3,2,1,4,7]
- Output: 3
- Explanation: The longest common subarray is [3, 2, 1].
Constraints:
- 1 <= len(A), len(B) <= 1000
- 0 <= A[i], B[j] < 100
# Approach
Note that the problem refers to subarrays, which are actually contiguous subsequences.
To find the longest repeated subarray in two arrays, a brute-force solution would involve two nested loops to determine the starting positions in each array, followed by another loop (either for or while) to compare elements starting from the two initial positions to measure the length of the repeated subarray.
This problem is a classic one that can be solved using dynamic programming. By using a two-dimensional array to keep track of all comparison scenarios between the arrays, it becomes easier to form the recurrence formula. The dynamic programming five-step analysis is as follows:
- Define the dp array (dp table) and the definition of the indices.
dp[i][j]: represents the length of the longest repeated subarray ending with A[i-1] and B[j-1]. (Note: "ending with A[i-1]" implies the subarray ends specifically at A[i-1].)
Observant readers might wonder what dp[0][0] represents. It certainly can't mean the subarray ending with an index of -1 for array A.
The definition of dp[i][j] dictates that when iterating over the dp table, i and j should both start from 1.
Someone might ask, can't we define dp[i][j] as the longest repeated subarray ending with A[i] and B[j]? Sure you can! But it would be more cumbersome to implement, requiring special handling of the initialization. In the extension section below this explanation, I've provided code and analysis for a second definition approach to the dp array, allowing for comparison.
- Determine the recurrence formula.
According to the definition of dp[i][j], the state of dp[i][j] can only be derived from dp[i-1][j-1].
That is, when A[i-1] and B[j-1] are equal, dp[i][j] = dp[i-1][j-1] + 1;
From the recurrence formula, we can see that the iteration over i and j should start from 1!
- How to initialize the dp array.
Based on the definition of dp[i][j], dp[i][0] and dp[0][j] are actually not meaningful!
However, dp[i][0] and dp[0][j] need initial values in order to align with the recurrence formula dp[i][j] = dp[i-1][j-1] + 1.
Thus, dp[i][0] and dp[0][j] are initialized to 0.
Consider the example: If A[0] equals B[0], then dp[1][1] = dp[0][0] + 1. With dp[0][0] initialized to 0, the recurrence gradually accumulates.
- Determine the iteration order.
Use an outer loop to iterate over A and an inner loop to iterate over B.
Can we swap them, iterating B on the outside and A on the inside? Yes, it's possible, but here we'll use A on the outside and B on the inside for consistency.
Additionally, the problem requires the length of the longest subarray. Therefore, during iteration, we should keep track of the maximum value of dp[i][j].
Here's the code:
for (int i = 1; i <= nums1.size(); i++) {
for (int j = 1; j <= nums2.size(); j++) {
if (nums1[i - 1] == nums2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
}
if (dp[i][j] > result) result = dp[i][j];
}
}
2
3
4
5
6
7
8
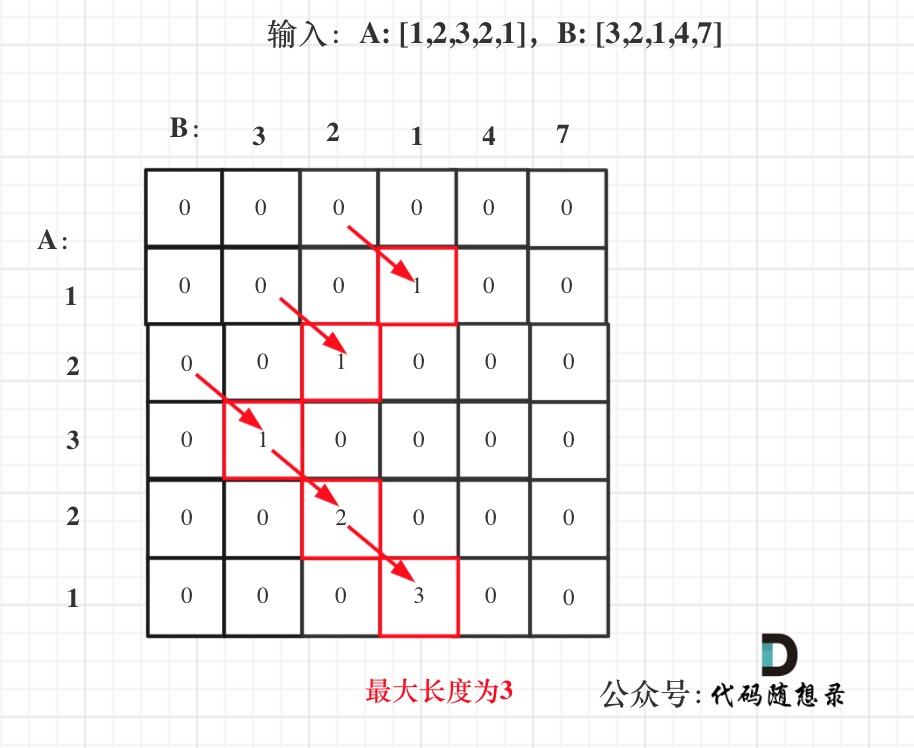
- Illustrate the dp array with an example.
Take the example from the problem statement, A: [1,2,3,2,1], B: [3,2,1,4,7], and visualize the state changes in the dp array as follows:
After completing the five-step analysis, here is the C++ code:
// Version 1
class Solution {
public:
int findLength(vector<int>& nums1, vector<int>& nums2) {
vector<vector<int>> dp (nums1.size() + 1, vector<int>(nums2.size() + 1, 0));
int result = 0;
for (int i = 1; i <= nums1.size(); i++) {
for (int j = 1; j <= nums2.size(); j++) {
if (nums1[i - 1] == nums2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
}
if (dp[i][j] > result) result = dp[i][j];
}
}
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
- Time Complexity: O(n × m), where n is the length of A, m is the length of B
- Space Complexity: O(n × m)
# Rolling Array
In the figure below:
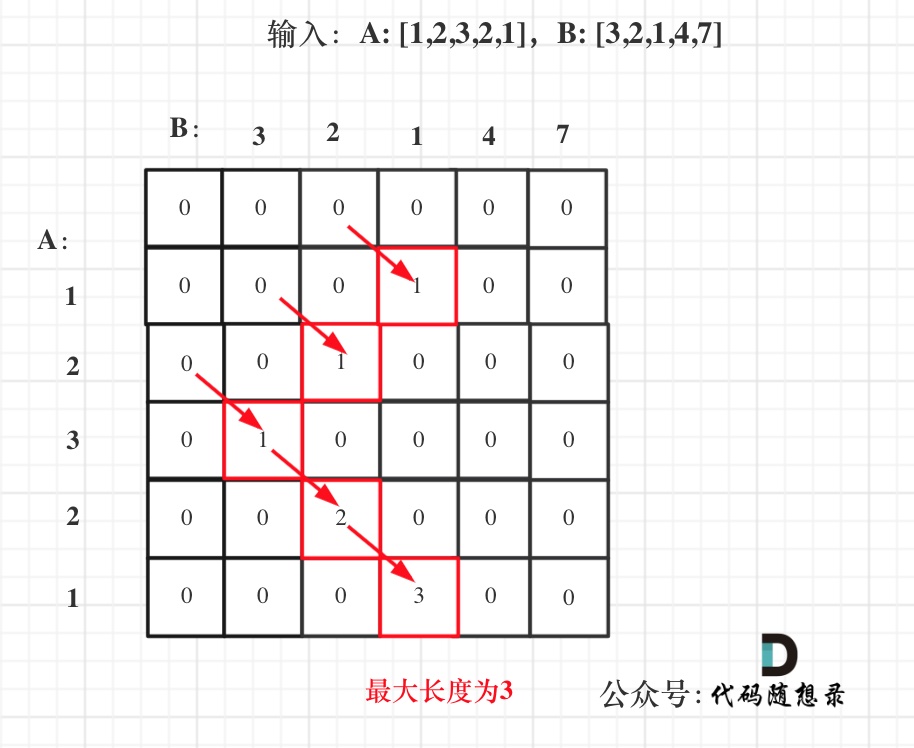
We can see that dp[i][j] is derived from dp[i-1][j-1]. This allows us to compress it into a one-dimensional array, meaning dp[j] is derived from dp[j-1].
Effectively, the state of dp[i-1][j] is copied to dp[i][j] for continued use.
Hence, when iterating the B array, it has to be backward to avoid overwriting existing data.
// Version 2
class Solution {
public:
int findLength(vector<int>& A, vector<int>& B) {
vector<int> dp(vector<int>(B.size() + 1, 0));
int result = 0;
for (int i = 1; i <= A.size(); i++) {
for (int j = B.size(); j > 0; j--) {
if (A[i - 1] == B[j - 1]) {
dp[j] = dp[j - 1] + 1;
} else dp[j] = 0; // Note: when not equal, set to 0
if (dp[j] > result) result = dp[j];
}
}
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
- Time Complexity: $O(n × m)$, where n is the length of A, m is the length of B
- Space Complexity: $O(m)$
# Extension
Earlier we discussed why the dp array is defined as: using the subarray ending with A[i-1] and B[j-1], with the longest repeated subarray length being dp[i][j].
But what about defining dp[i][j] as ending with A[i] and B[j]? Of course, you can do that, it just becomes slightly more cumbersome to implement.
When defining dp[i][j] as ending with A[i] and B[j], you must initialize the first row and first column. For instance, if nums1[i] is equal to nums2[0], then dp[i][0] should be initialized to 1, because the longest repeated subarray under those conditions is 1. The same logic applies for nums2[j] and nums1[0].
Here's the code for that:
// Version 3
class Solution {
public:
int findLength(vector<int>& nums1, vector<int>& nums2) {
vector<vector<int>> dp (nums1.size() + 1, vector<int>(nums2.size() + 1, 0));
int result = 0;
// Initialize the first row and first column
for (int i = 0; i < nums1.size(); i++) if (nums1[i] == nums2[0]) dp[i][0] = 1;
for (int j = 0; j < nums2.size(); j++) if (nums1[0] == nums2[j]) dp[0][j] = 1;
for (int i = 0; i < nums1.size(); i++) {
for (int j = 0; j < nums2.size(); j++) {
if (nums1[i] == nums2[j] && i > 0 && j > 0) { // Prevent negative indices
dp[i][j] = dp[i - 1][j - 1] + 1;
}
if (dp[i][j] > result) result = dp[i][j];
}
}
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
You will notice this method requires additional assignment code for the initialization.
For the collection of all results using if (dp[i][j] > result) result = dp[i][j];, both nested for-loops must begin from 0. This necessitates adding an extra check && i > 0 && j > 0.
For beginners with an insecure foundation, there might be confusion regarding why the loop includes i=0,j=0 rather than commencing with i=1,j=1 given the recurrence relation. The reason for this is that not starting from i=0,j=0 might miss some outcomes:
nums1 = [70,39,25,40,7]
nums2 = [52,20,67,5,31]
2
Incidentally, if you're inclined, you might use the following code which aligns with the same thinking of the previous C++ version:
class Solution {
public int findLength(int[] nums1, int[] nums2) {
int len1 = nums1.length;
int len2 = nums2.length;
int[][] result = new int[len1][len2];
int maxresult = Integer.MIN_VALUE;
for(int i=0;i<len1;i++){
if(nums1[i] == nums2[0])
result[i][0] = 1;
if(maxresult<result[i][0])
maxresult = result[i][0];
}
for(int j=0;j<len2;j++){
if(nums1[0] == nums2[j])
result[0][j] = 1;
if(maxresult<result[0][j])
maxresult = result[0][j];
}
for(int i=1;i<len1;i++){
for(int j=1;j<len2;j++){
if(nums1[i]==nums2[j])
result[i][j] = result[i-1][j-1]+1;
if(maxresult<result[i][j])
maxresult = result[i][j];
}
}
return maxresult;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
For beginners, be sure to understand what data is being initialized within the dp array.
Overall, this approach does involve writing extra code compared to Version 1 while also being a bit more logically complex. The advantage is that it provides a more intuitive definition for the dp array.
# Other Language Versions
# Java:
// Version 1
class Solution {
public int findLength(int[] nums1, int[] nums2) {
int result = 0;
int[][] dp = new int[nums1.length + 1][nums2.length + 1];
for (int i = 1; i <= nums1.length; i++) {
for (int j = 1; j <= nums2.length; j++) {
if (nums1[i - 1] == nums2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
result = Math.max(result, dp[i][j]);
}
}
}
return result;
}
}
// Version 2: Rolling array
class Solution {
public int findLength(int[] nums1, int[] nums2) {
int[] dp = new int[nums2.length + 1];
int result = 0;
for (int i = 1; i <= nums1.length; i++) {
for (int j = nums2.length; j > 0; j--) {
if (nums1[i - 1] == nums2[j - 1]) {
dp[j] = dp[j - 1] + 1;
} else {
dp[j] = 0;
}
result = Math.max(result, dp[j]);
}
}
return result;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
# Python:
2D DP
class Solution:
def findLength(self, nums1: List[int], nums2: List[int]) -> int:
# Create a 2D array dp to record the length of the longest common subarray
dp = [[0] * (len(nums2) + 1) for _ in range(len(nums1) + 1)]
# Record the length of the longest common subarray
result = 0
# Traverse through the nums1 array
for i in range(1, len(nums1) + 1):
# Traverse through the nums2 array
for j in range(1, len(nums2) + 1):
# If nums1[i-1] == nums2[j-1]
if nums1[i - 1] == nums2[j - 1]:
# The length of the longest common subarray at this position is the previous position's length plus one
dp[i][j] = dp[i - 1][j - 1] + 1
# Update the length of the longest common subarray
if dp[i][j] > result:
result = dp[i][j]
# Return the length of the longest common subarray
return result
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
1D DP
class Solution:
def findLength(self, nums1: List[int], nums2: List[int]) -> int:
# Create a 1D array dp to store the length of the longest common subarray
dp = [0] * (len(nums2) + 1)
# Record the length of the longest common subarray
result = 0
# Traverse through the nums1 array
for i in range(1, len(nums1) + 1):
# Variable to save the value of the previous position
prev = 0
# Traverse through the nums2 array
for j in range(1, len(nums2) + 1):
# Save the current value as it will be updated in the following
current = dp[j]
# If nums1[i-1] == nums2[j-1]
if nums1[i - 1] == nums2[j - 1]:
# The length of the longest common subarray at this position is the length of the previous position plus one
dp[j] = prev + 1
# Update the length of the longest common subarray
if dp[j] > result:
result = dp[j]
else:
# If not equal, set the current position to zero
dp[j] = 0
# Update the prev variable to the current position's value for use in the next iteration
prev = current
# Return the length of the longest common subarray
return result
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
2D DP Extension
class Solution:
def findLength(self, nums1: List[int], nums2: List[int]) -> int:
# Create a 2D array dp to record the length of the longest common subarray
dp = [[0] * (len(nums2) + 1) for _ in range(len(nums1) + 1)]
# Record the length of the longest common subarray
result = 0
# Initialize the first row and first column
for i in range(len(nums1)):
if nums1[i] == nums2[0]:
dp[i + 1][1] = 1
for j in range(len(nums2)):
if nums1[0] == nums2[j]:
dp[1][j + 1] = 1
# Fill in the dp array
for i in range(1, len(nums1) + 1):
for j in range(1, len(nums2) + 1):
if nums1[i - 1] == nums2[j - 1]:
# If nums1[i-1] and nums2[j-1] are equal, the length of the longest common subarray at this position is the value at the top left plus one
dp[i][j] = dp[i - 1][j - 1] + 1
if dp[i][j] > result:
# Update the length of the longest common subarray
result = dp[i][j]
# Return the length of the longest common subarray
return result
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# Go:
func findLength(A []int, B []int) int {
m, n := len(A), len(B)
res := 0
dp := make([][]int, m+1)
for i := 0; i <= m; i++ {
dp[i] = make([]int, n+1)
}
for i := 1; i <= m; i++ {
for j := 1; j <= n; j++ {
if A[i-1] == B[j-1] {
dp[i][j] = dp[i-1][j-1] + 1
}
if dp[i][j] > res {
res = dp[i][j]
}
}
}
return res
}
// Rolling array
func findLength(nums1 []int, nums2 []int) int {
n, m, res := len(nums1), len(nums2), 0
dp := make([]int, m+1)
for i := 1; i <= n; i++ {
for j := m; j >= 1; j-- {
if nums1[i-1] == nums2[j-1] {
dp[j] = dp[j-1] + 1
} else {
dp[j] = 0 // Note: when not equal, set to 0
}
res = max(res, dp[j])
}
}
return res
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
# JavaScript:
Dynamic Programming
const findLength = (A, B) => {
// Length of arrays A and B
const [m, n] = [A.length, B.length];
// Initialize dp array, all initialized to 0
const dp = new Array(m + 1).fill(0).map(x => new Array(n + 1).fill(0));
// Initialize maximum length to 0
let res = 0;
for (let i = 1; i <= m; i++) {
for (let j = 1; j <= n; j++) {
// Upon encountering A[i - 1] === B[j - 1], update dp array
if (A[i - 1] === B[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
}
// Update res
res = dp[i][j] > res ? dp[i][j] : res;
}
}
// Upon completion of iteration, return res
return res;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Rolling Array
const findLength = (nums1, nums2) => {
let len1 = nums1.length, len2 = nums2.length;
// dp[i][j]: the length of longest common subarray ending with nums1[i-1], nums2[j-1]
let dp = new Array(len2+1).fill(0);
let res = 0;
for (let i = 1; i <= len1; i++) {
for (let j = len2; j > 0; j--) {
if (nums1[i-1] === nums2[j-1]) {
dp[j] = dp[j-1] + 1;
} else {
dp[j] = 0;
}
res = Math.max(res, dp[j]);
}
}
return res;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# TypeScript:
Dynamic Programming:
function findLength(nums1: number[], nums2: number[]): number {
/**
dp[i][j]: the length of the longest repeated subarray ending with nums[i-1] and nums[j-1]
*/
const length1: number = nums1.length,
length2: number = nums2.length;
const dp: number[][] = new Array(length1 + 1).fill(0)
.map(_ => new Array(length2 + 1).fill(0));
let resMax: number = 0;
for (let i = 1; i <= length1; i++) {
for (let j = 1; j <= length2; j++) {
if (nums1[i - 1] === nums2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
resMax = Math.max(resMax, dp[i][j]);
}
}
}
return resMax;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Rolling Array:
function findLength(nums1: number[], nums2: number[]): number {
const length1: number = nums1.length,
length2: number = nums2.length;
const dp: number[] = new Array(length1 + 1).fill(0);
let resMax: number = 0;
for (let i = 1; i <= length1; i++) {
for (let j = length2; j >= 1; j--) {
if (nums1[i - 1] === nums2[j - 1]) {
dp[j] = dp[j - 1] + 1;
resMax = Math.max(resMax, dp[j]);
} else {
dp[j] = 0;
}
}
}
return resMax;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Rust:
Rolling Array
impl Solution {
pub fn find_length(nums1: Vec<i32>, nums2: Vec<i32>) -> i32 {
let (mut res, mut dp) = (0, vec![0; nums2.len()]);
for n1 in nums1 {
for j in (0..nums2.len()).rev() {
if n1 == nums2[j] {
dp[j] = if j == 0 { 1 } else { dp[j - 1] + 1 };
res = res.max(dp[j]);
} else {
dp[j] = 0;
}
}
}
res
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# C:
int findLength(int* nums1, int nums1Size, int* nums2, int nums2Size) {
int dp[nums1Size + 1][nums2Size + 1];
memset(dp, 0, sizeof(dp));
int result = 0;
for (int i = 1; i <= nums1Size; ++i) {
for (int j = 1; j <= nums2Size; ++j) {
if(nums1[i - 1] == nums2[j - 1]){
dp[i][j] = dp[i - 1][j - 1] + 1;
}
if(dp[i][j] > result){
result = dp[i][j];
}
}
}
return result;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# Cangjie
func findLength(nums1: Array<Int64>, nums2: Array<Int64>): Int64 {
let n = nums1.size
let m = nums2.size
let dp = Array(n + 1, {_ => Array(m + 1, item: 0)})
var res = 0
for (i in 1..=n) {
for (j in 1..=m) {
if (nums1[i - 1] == nums2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1
}
res = max(res, dp[i][j])
}
}
return res
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
