# 1035. Uncrossed Lines
LeetCode Problem Link (opens new window)
On two separate horizontal lines, write the integers from nums1 and nums2 in the given order.
You can draw connecting lines between numbers nums1[i] and nums2[j] only if:
nums1[i] == nums2[j]- and the connecting lines do not intersect (non-horizontal).
Note that even at the endpoints, lines cannot intersect: each number can only belong to one line.
Draw lines in this manner and return the maximum number of connecting lines possible.

# Thought Process
I believe many readers might not have a clear idea when first seeing this problem, so let's analyze it step by step.
You are to draw lines connecting nums1[i] and nums2[j] whenever nums1[i] == nums2[j], and ensure that the lines do not intersect!
The fact that the lines do not intersect implies that we are finding a subsequence of nums1 that is also present in nums2, with the order preserved. If the order is preserved, the lines connecting the matching numbers will not intersect.
Consider the example where nums1 = [1,4,2] and nums2 = [1,2,4], which results in intersecting lines as shown:
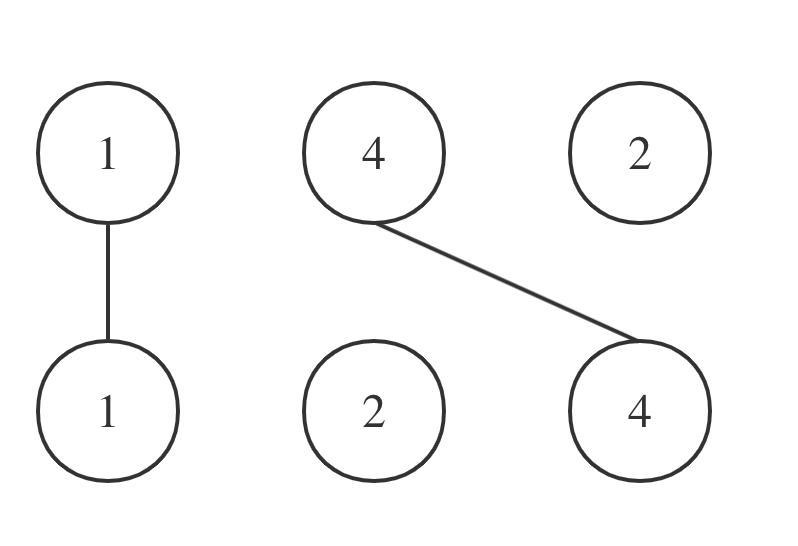
Actually, this means the longest common subsequence of nums1 and nums2 is [1,4] with a length of 2. This common subsequence has to maintain the relative order (i.e., if number 4 appears after number 1 in the sequence from nums1, then it must do so in nums2 as well).
After this analysis, you can see: The problem of finding the maximum number of connecting lines is actually about finding the length of the longest common subsequence of the two strings!
Therefore, this problem is essentially identical to the problem 1143. Longest Common Subsequence (opens new window).
It's so similar that you can just rename the strings and reuse the same code from the previous problem.
Since this problem is about finding the length of the longest common subsequence, I will not go over the five dynamic programming steps here, as we have already covered them in a previous solution. If you need to refresh your memory on the longest common subsequence, please refer to: 1143. Longest Common Subsequence (opens new window).
Here is the solution code:
class Solution {
public:
int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
vector<vector<int>> dp(nums1.size() + 1, vector<int>(nums2.size() + 1, 0));
for (int i = 1; i <= nums1.size(); i++) {
for (int j = 1; j <= nums2.size(); j++) {
if (nums1[i - 1] == nums2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[nums1.size()][nums2.size()];
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
- Time Complexity: O(n * m)
- Space Complexity: O(n * m)
# Summary
As you can see from the code, this problem is fundamentally about finding the longest common subsequence between two strings. However, if you haven't solved 1143. Longest Common Subsequence (opens new window) before, this problem can be quite challenging.
This is why I chose to introduce 1143. Longest Common Subsequence (opens new window) before tackling this problem. A correct sequence of solving problems is crucial for effective learning in algorithms!
This ordering is something I've deduced after solving numerous problems (both ACM and LeetCode), and I encourage you to reflect on it.
# Other Language Versions
# Java:
class Solution {
public int maxUncrossedLines(int[] nums1, int[] nums2) {
int len1 = nums1.length;
int len2 = nums2.length;
int[][] dp = new int[len1 + 1][len2 + 1];
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
if (nums1[i - 1] == nums2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[len1][len2];
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# Python:
class Solution:
def maxUncrossedLines(self, nums1: List[int], nums2: List[int]) -> int:
dp = [[0] * (len(nums2)+1) for _ in range(len(nums1)+1)]
for i in range(1, len(nums1)+1):
for j in range(1, len(nums2)+1):
if nums1[i-1] == nums2[j-1]:
dp[i][j] = dp[i-1][j-1] + 1
else:
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
return dp[-1][-1]
2
3
4
5
6
7
8
9
10
# Go:
func maxUncrossedLines(nums1 []int, nums2 []int) int {
dp := make([][]int, len(nums1) + 1)
for i := range dp {
dp[i] = make([]int, len(nums2) + 1)
}
for i := 1; i <= len(nums1); i++ {
for j := 1; j <= len(nums2); j++ {
if (nums1[i - 1] == nums2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1
} else {
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
}
}
}
return dp[len(nums1)][len(nums2)]
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# Rust:
impl Solution {
pub fn max_uncrossed_lines(nums1: Vec<i32>, nums2: Vec<i32>) -> i32 {
let mut dp = vec![vec![0; nums2.len() + 1]; nums1.len() + 1];
for (i, num1) in nums1.iter().enumerate() {
for (j, num2) in nums2.iter().enumerate() {
if num1 == num2 {
dp[i + 1][j + 1] = dp[i][j] + 1;
} else {
dp[i + 1][j + 1] = dp[i][j + 1].max(dp[i + 1][j]);
}
}
}
dp[nums1.len()][nums2.len()]
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Rolling Array
impl Solution {
pub fn max_uncrossed_lines(nums1: Vec<i32>, nums2: Vec<i32>) -> i32 {
let mut dp = vec![0; nums2.len() + 1];
for num1 in nums1 {
let mut prev = 0;
for (j, &num2) in nums2.iter().enumerate() {
let temp = dp[j + 1];
if num1 == num2 {
// Use the previous state to prevent redundant calculations
dp[j + 1] = prev + 1;
} else {
dp[j + 1] = dp[j + 1].max(dp[j]);
}
prev = temp;
}
}
dp[nums2.len()]
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# JavaScript:
const maxUncrossedLines = (nums1, nums2) => {
// Lengths of two arrays
const [m, n] = [nums1.length, nums2.length];
// Create and initialize dp array to 0
const dp = new Array(m + 1).fill(0).map(x => new Array(n + 1).fill(0));
for (let i = 1; i <= m; i++) {
for (let j = 1; j <= n; j++) {
// Update dp[i][j] based on two cases
if (nums1[i - 1] === nums2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
// Return the element at the bottom right of the dp array
return dp[m][n];
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# TypeScript:
Two-dimensional array
function maxUncrossedLines(nums1: number[], nums2: number[]): number {
/**
dp[i][j]: max number of connecting lines using the first i-1 elements of nums1 and j-1 elements of nums2
*/
const length1: number = nums1.length,
length2: number = nums2.length;
const dp: number[][] = new Array(length1 + 1).fill(0)
.map(_ => new Array(length2 + 1).fill(0));
for (let i = 1; i <= length1; i++) {
for (let j = 1; j <= length2; j++) {
if (nums1[i - 1] === nums2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[length1][length2];
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Rolling array
function maxUncrossedLines(nums1: number[], nums2: number[]): number {
const len1 = nums1.length
const len2 = nums2.length
const dp: number[] = new Array(len2 + 1).fill(0)
for (let i = 1; i <= len1; i++) {
let prev: number = 0;
let temp: number = 0;
for (let j = 1; j <= len2; j++) {
// Back up the current state (updated by previous iteration)
temp = dp[j]
// prev represents dp[j-1] (including past state)
// If only using dp[j-1], it wouldn't carry the past state
if (nums1[i - 1] === nums2[j - 1]) dp[j] = prev + 1
// dp[j] refers to previous dp[i][j-1], dp[j-1] refers to dp[i-1][j]
else dp[j] = Math.max(dp[j], dp[j - 1])
// Update the parameter with the current layer state for next state
prev = temp
}
}
return dp[len2]
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
