121. Best Time to Buy and Sell Stock

LeetCode Problem Link (opens new window)

Given an array prices where prices[i] is the price of a given stock on the i-th day.

You can only choose to buy one share of the stock on one day and sell it on a different future day. Design an algorithm to find the maximum profit you can achieve.

Return the maximum profit you can achieve from this transaction. If you cannot achieve any profit, return 0.

• Example 1:

• Input: [7,1,5,3,6,4]

• Output: 5
  Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5. Note that you cannot sell before you buy.

• Example 2:

• Input: prices = [7,6,4,3,1]

• Output: 0
  Explanation: In this case, no transaction is done, so the maximum profit is 0.

Thought Process

Brute Force

The most straightforward solution is brute force, which involves finding the optimal price interval.

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int result = 0;
        for (int i = 0; i < prices.size(); i++) {
            for (int j = i + 1; j < prices.size(); j++){
                result = max(result, prices[j] - prices[i]);
            }
        }
        return result;
    }
};

• Time complexity: O(n^2)
• Space complexity: O(1)

This method will obviously exceed time limits.

Greedy

Since the stock can be bought and sold only once, a natural greedy approach is to find the leftmost minimum price and the rightmost maximum price, with the difference being the maximum profit.

C++ code is as follows:

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int low = INT_MAX;
        int result = 0;
        for (int i = 0; i < prices.size(); i++) {
            low = min(low, prices[i]);  // Find the leftmost lowest price
            result = max(result, prices[i] - low); // Get the maximum interval profit
        }
        return result;
    }
};

• Time complexity: O(n)
• Space complexity: O(1)

Dynamic Programming

The five steps for dynamic programming analysis are as follows:

1. Define the dp array (or table) and the meaning of the index

dp[i][0] represents the maximum cash on the i-th day while holding stock. You may wonder, in this problem, can there be any cash left after buying once?

Initially, cash is 0. So if you buy stock on the i-th day, the cash would be -prices[i], which is a negative number.

dp[i][1] represents the maximum cash on the i-th day without holding stock.

Note that it says "holding," which does not necessarily mean "buying"! It could also mean maintaining the state of having bought it the previous day.

Many confuse "holding" with "buying."

Further explanation follows in the recursive formula analysis.

2. Determine the recursive formula

If holding stock on the i-th day, then dp[i][0], can be derived from two states:

• The state where the previous day already held stock, keep this state, cash remains as yesterday, i.e., dp[i - 1][0]
• Buy stock today, cash left after buying at today's price, i.e., -prices[i]

Thus, choose the largest cash: dp[i][0] = max(dp[i - 1][0], -prices[i]);

If not holding stock on the i-th day, dp[i][1], can also be derived:

• The state where the previous day did not hold stock, keep this state, cash remains as yesterday, i.e., dp[i - 1][1]
• Sell stock today, cash gained by selling at today's price, i.e., prices[i] + dp[i - 1][0]

Similarly, take the largest, dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);

Thus, the recursive formula:

dp[i][0] = max(dp[i - 1][0], -prices[i]);
dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);

3. Initialize the dp array

From the recursive formula, dp[i][0] is derived from dp[i - 1], so dp[0][0] and dp[0][1] must be set.

On the 0th day, holding stock means buying it as there's no previous day, so dp[0][0] = -prices[0];

Not holding stock on the 0th day means cash is 0, so dp[0][1] = 0;

4. Determine the traversal order

The recursive formula shows that dp[i] is derived from dp[i - 1], a forward traversal is needed.

5. Example to derive the dp array

In Example 1, Input: [7,1,5,3,6,4] results in the dp states as follows:

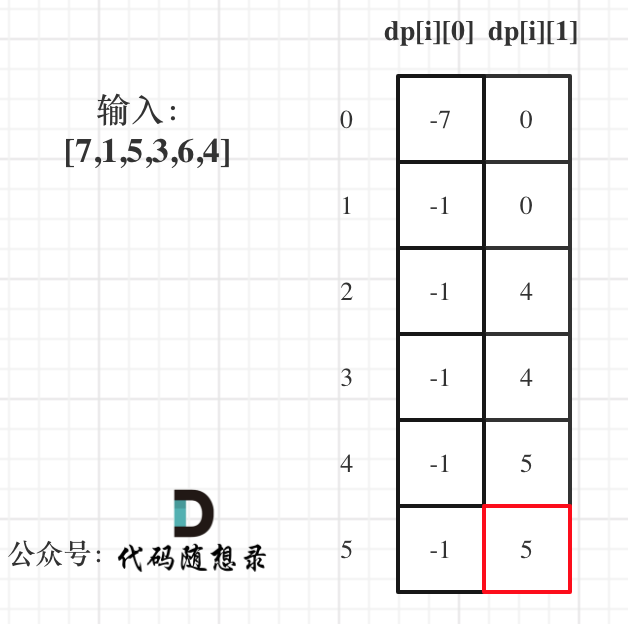
dp[5][1] is the final result.

Why not dp[5][0]?

Because in this problem, the state without holding stock must yield more cash than the state with holding stock!

Analysis complete, C++ code is as follows:

// Version 1
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int len = prices.size();
        if (len == 0) return 0;
        vector<vector<int>> dp(len, vector<int>(2));
        dp[0][0] -= prices[0];
        dp[0][1] = 0;
        for (int i = 1; i < len; i++) {
            dp[i][0] = max(dp[i - 1][0], -prices[i]);
            dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);
        }
        return dp[len - 1][1];
    }
};

• Time complexity: O(n)
• Space complexity: O(n)

The recursive formula shows dp[i] only depends on the state from dp[i - 1].

dp[i][0] = max(dp[i - 1][0], -prices[i]);
dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);

Therefore, only two states need recording, this can be optimized with a rolling array:

// Version 2
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int len = prices.size();
        vector<vector<int>> dp(2, vector<int>(2)); // Only a 2 * 2 array
        dp[0][0] -= prices[0];
        dp[0][1] = 0;
        for (int i = 1; i < len; i++) {
            dp[i % 2][0] = max(dp[(i - 1) % 2][0], -prices[i]);
            dp[i % 2][1] = max(dp[(i - 1) % 2][1], prices[i] + dp[(i - 1) % 2][0]);
        }
        return dp[(len - 1) % 2][1];
    }
};

• Time complexity: O(n)
• Space complexity: O(1)

Start with Version 1, and then optimize to Version 2 based on Version 1. Directly writing Version 2 might lead to bugs.

Thus, Version 2 should evolve from Version 1.

Versions in Other Languages

Java:

Greedy approach:

class Solution {
    public int maxProfit(int[] prices) {
        // find the lowest purchase price
        int low = Integer.MAX_VALUE;
        // res updates until the array is fully traversed
        int res = 0;
        for(int i = 0; i < prices.length; i++){
            low = Math.min(prices[i], low);
            res = Math.max(prices[i] - low, res);
        }
        return res;
    }
}

Dynamic Programming: Version 1

// Solution 1
class Solution {
    public int maxProfit(int[] prices) {
        if (prices == null || prices.length == 0) return 0;
        int length = prices.length;
        // dp[i][0] represents the maximum profit on the i-th day while holding stocks
        // dp[i][1] represents the maximum profit on the i-th day without holding stocks
        int[][] dp = new int[length][2];
        int result = 0;
        dp[0][0] = -prices[0];
        dp[0][1] = 0;
        for (int i = 1; i < length; i++) {
            dp[i][0] = Math.max(dp[i - 1][0], -prices[i]);
            dp[i][1] = Math.max(dp[i - 1][0] + prices[i], dp[i - 1][1]);
        }
        return dp[length - 1][1];
    }
}

Dynamic Programming: Version 2 (Using a 2-dimensional array, similar to the previous theme, below is a more optimized version using a one-dimensional array)

class Solution {
    public int maxProfit(int[] prices) {
        int len = prices.length;
        int dp[][] = new int[2][2];
        
        dp[0][0] = - prices[0];
        dp[0][1] = 0;

        for (int i = 1; i < len; i++){
            dp[i % 2][0] = Math.max(dp[(i - 1) % 2][0], - prices[i]);
            dp[i % 2][1] = Math.max(dp[(i - 1) % 2][1], prices[i] + dp[(i - 1) % 2][0]);
        }
        return dp[(len - 1) % 2][1];
    }
}

Dynamic Programming: Version 2 (Using a one-dimensional array)

class Solution {
  public int maxProfit(int[] prices) {
    int[] dp = new int[2];
    // Record a transaction, a transaction has buy and sell two states
    // 0 means holding, 1 means selling
    dp[0] = -prices[0];
    dp[1] = 0;
    // Reference Fibonacci problem optimization method
    // Iterate from i=1, with prices.length days, so i<=prices.length
    for (int i = 1; i <= prices.length; i++) {
      // Previous day holding; or bought today
      dp[0] = Math.max(dp[0], -prices[i - 1]);
      // If dp[0] is updated, then dp[1] is updated to positive dp[1]
      // So using dp[0] here is fine as well
      // Previous day selling; or sold today, the previous day must have been holding
      dp[1] = Math.max(dp[1], dp[0] + prices[i - 1]);
    }
    return dp[1];
  }
}

Python:

Greedy approach:

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        low = float("inf")
        result = 0
        for i in range(len(prices)):
            low = min(low, prices[i]) # Find the leftmost lowest price
            result = max(result, prices[i] - low) # Directly get the maximum interval profit
        return result

Dynamic Programming: Version 1

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        length = len(prices)
        if length == 0:
            return 0
        dp = [[0] * 2 for _ in range(length)]
        dp[0][0] = -prices[0]
        dp[0][1] = 0
        for i in range(1, length):
            dp[i][0] = max(dp[i-1][0], -prices[i])
            dp[i][1] = max(dp[i-1][1], prices[i] + dp[i-1][0])
        return dp[-1][1]

Dynamic Programming: Version 2

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        length = len(prices)
        dp = [[0] * 2 for _ in range(2)] # Note that here only a 2 * 2 matrix is initialized
        dp[0][0] = -prices[0]
        dp[0][1] = 0
        for i in range(1, length):
            dp[i % 2][0] = max(dp[(i-1) % 2][0], -prices[i])
            dp[i % 2][1] = max(dp[(i-1) % 2][1], prices[i] + dp[(i-1) % 2][0])
        return dp[(length-1) % 2][1]

Dynamic Programming: Version 3

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        length = len(prices)
        dp0, dp1 = -prices[0], 0 # Only two constants are maintained here as updating dp0 doesn't affect dp1
        for i in range(1, length):
            dp1 = max(dp1, dp0 + prices[i])
            dp0 = max(dp0, -prices[i])
        return dp1

Go:

Greedy approach:

func maxProfit(prices []int) int {
    min := prices[0]
    res := 0
    for i := 1; i < len(prices); i++ {
        if prices[i] - min > res {
            res = prices[i]-min
        }
        if min > prices[i] {
            min = prices[i]
        }
    }
    return res
}

Dynamic Programming: Version 1

func maxProfit(prices []int) int {
	length := len(prices)
	if length == 0{return 0}
	dp := make([][]int,length)
	for i := 0; i < length; i++ {
		dp[i] = make([]int, 2)
	}
	dp[0][0] = -prices[0]
	dp[0][1] = 0
	for i := 1; i < length; i++ {
		dp[i][0] = max(dp[i-1][0], -prices[i])
		dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i])
	}
	return dp[length-1][1]
}

func max(a, b int) int {
    if a > b {
        return a 
    }
    return b 
}

Dynamic Programming: Version 2

func maxProfit(prices []int) int {
    dp := [2][2]int{}
    dp[0][0] = -prices[0]   
    dp[0][1] = 0
    for i := 1; i < len(prices); i++ {
        dp[i%2][0] = max(dp[(i-1)%2][0], -prices[i])
        dp[i%2][1] = max(dp[(i-1)%2][1], dp[(i-1)%2][0]+prices[i])
    }

    return dp[(len(prices)-1)%2][1]
}

func max(a, b int) int {
    if a > b{
        return a 
    }

    return b
}

JavaScript:

Dynamic Programming

const maxProfit = prices => {
    const len = prices.length;
    // Create dp array
    const dp = new Array(len).fill([0, 0]);
    // Initialize dp array
    dp[0] = [-prices[0], 0];
    for (let i = 1; i < len; i++) {
        // Update dp[i]
        dp[i] = [
            Math.max(dp[i - 1][0], -prices[i]),
            Math.max(dp[i - 1][1], prices[i] + dp[i - 1][0]),
        ];
    }
    return dp[len - 1][1];
};

Greedy approach

var maxProfit = function(prices) {
    let lowerPrice = prices[0];// The key is to maintain this minimum (Greedy approach)
    let profit = 0;
    for(let i = 0; i < prices.length; i++){
        lowerPrice = Math.min(lowerPrice, prices[i]);// Greedily choose the leftmost minimum price
        profit = Math.max(profit, prices[i] - lowerPrice);// A single traversal can get the maximum profit
    }
    return profit;
};

TypeScript：

Greedy approach

function maxProfit(prices: number[]): number {
    if (prices.length === 0) return 0;
    let buy: number = prices[0];
    let profitMax: number = 0;
    for (let i = 1, length = prices.length; i < length; i++) {
        profitMax = Math.max(profitMax, prices[i] - buy);
        buy = Math.min(prices[i], buy);
    }
    return profitMax;
};

Dynamic Programming: Version 1

function maxProfit(prices: number[]): number {
    /**
        dp[i][0]: Maximum cash on the i-th day while holding stocks
        dp[i][1]: Maximum cash on the i-th day without holding stocks
     */
    const length = prices.length;
    if (length === 0) return 0;
    const dp: number[][] = [];
    dp[0] = [-prices[0], 0];
    for (let i = 1; i < length; i++) {
        dp[i] = [];
        dp[i][0] = Math.max(dp[i - 1][0], -prices[i]);
        dp[i][1] = Math.max(dp[i - 1][0] + prices[i], dp[i - 1][1]);
    }
    return dp[length - 1][1];
};

Dynamic Programming: Version 2

// dp[i][0] represents the most cash you can hold stocks by the i-th day
// dp[i][1] represents the most cash you can have without holding stocks by the i-th day
function maxProfit(prices: number[]): number {
    const dp:number[][] = Array(2).fill(0).map(item => Array(2));
    dp[0][0] = -prices[0];
    dp[0][1] = 0;
    
    for (let i = 1; i < prices.length; i++) {
        dp[i % 2][0] = Math.max(dp[(i - 1) % 2][0], -prices[i]);
        dp[i % 2][1] = Math.max(dp[(i - 1) % 2][1], dp[(i - 1) % 2][0] + prices[i]);
    }

    // Return the maximum cash without holding stocks
    return dp[(prices.length-1) % 2][1];
};

C#：

Greedy approach

public class Solution
{
    public int MaxProfit(int[] prices)
    {
        int min = Int32.MaxValue;
        int res = 0;
        for (int i = 0; i < prices.Length; i++)
        {
            min = Math.Min(prices[i], min);
            res = Math.Max(prices[i] - min, res);
        }
        return res;
    }
}

Dynamic Programming

public class Solution
{
	public int MaxProfit(int[] prices)
    {
        int[] dp = new int[2];
        int size = prices.Length;
        (dp[0], dp[1]) = (-prices[0], 0);
        for (int i = 0; i < size; i++)
        {
            dp[0] = Math.Max(dp[0], -prices[i]);
            dp[1] = Math.Max(dp[1], dp[0]+prices[i]);
        }
        return dp[1];
    }
}

C：

Greedy

#define max(a, b) ((a) > (b) ? (a) : (b))
#define min(a, b) ((a) > (b) ? (b) : (a))

int maxProfit(int* prices, int pricesSize) {
    int low = INT_MIN;
    int result = 0;
    for(int i = 0; i < pricesSize; i++){
        low = min(low, prices[i]);
        result = max(result, prices[i] - low);
    }
    return result;
}

Dynamic Programming

#define max(a, b) ((a) > (b) ? (a) : (b))

int maxProfit(int* prices, int pricesSize){
    if(pricesSize == 0){
        return 0;
    }
    // Initialize dp
    int ** dp = malloc(sizeof (int *) * pricesSize);
    for(int i = 0; i < pricesSize; i++){
        dp[i] = malloc(sizeof (int ) * 2);
    }
    // Index 0 denotes maximum cash holding stocks, index 1 denotes cash without holding stocks
    dp[0][0] = -prices[0];
    dp[0][1] = 0;
    for(int i = 1; i < pricesSize; i++){
        dp[i][0] = max(dp[i - 1][0], - prices[i]);
        dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);
    }
    return dp[pricesSize - 1][1];
}

Rust:

Greedy

impl Solution {
    pub fn max_profit(prices: Vec<i32>) -> i32 {
        let (mut low, mut res) = (i32::MAX, 0);
        for p in prices {
            low = p.min(low);
            res = res.max(p - low);
        }
        res
    }
}

Dynamic Programming

impl Solution {
    pub fn max_profit(prices: Vec<i32>) -> i32 {
        let mut dp = vec![-prices[0], 0];
        for p in prices {
            dp[0] = dp[0].max(-p);
            dp[1] = dp[1].max(dp[0] + p);
        }
        dp[1]
    }
}