# 337. House Robber III
LeetCode Problem Link (opens new window)
After robbing a series of houses along a street and circling those houses, the thief now discovers a new area to target for burglary. This area has only one entrance, referred to as the "root". Apart from the "root", each house is connected to exactly one "parent" house. After some investigation, the intelligent thief realizes that "the arrangement of all the houses in this area resembles a binary tree". If two directly connected houses are robbed on the same night, an alarm will automatically sound.
Calculate the maximum amount of money the thief can rob in one night without triggering the alarm.
# Approach
This problem is similar to 198.House Robber (opens new window) and 213.House Robber II (opens new window), except this one uses a tree structure.
If you're not familiar with tree traversal, this problem can be quite challenging.
For trees, the first thing that comes to mind is the traversal method: pre-order, in-order, post-order (depth-first search), or level-order traversal (breadth-first search).
This problem requires post-order traversal because we need the return values of recursion functions for the next step of the computation.
Like 198.House Robber and 213.House Robber II, the key is to decide whether to rob the current node or not.
If the current node is robbed, the two children node cannot be robbed. If the current node is not robbed, then we can consider robbing the left and right children (note that we say "consider" here).
# Brute Force Recursive Solution
class Solution {
public:
int rob(TreeNode* root) {
if (root == NULL) return 0;
if (root->left == NULL && root->right == NULL) return root->val;
// Rob the parent node
int val1 = root->val;
if (root->left) val1 += rob(root->left->left) + rob(root->left->right);
if (root->right) val1 += rob(root->right->left) + rob(root->right->right);
// Do not rob the parent node
int val2 = rob(root->left) + rob(root->right);
return max(val1, val2);
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
- Time Complexity: O(n^2), this time complexity is not quite standard and hard to precisely define, as nodes further down are recalculated more often.
- Space Complexity: O(log n), considering the recursive system stack space.
Of course, the above code will time out because there are repeated calculations in the recursion process.
We calculate the subtree with the root's four grandchildren (left and right children's children) as the header node and also calculate the subtree with the root's left and right children as header nodes. When calculating the children, the grandchildren are recalculated.
# Memoized Recursion
So we can use a map to save the already calculated results, so if the grandchildren are already calculated, we can reuse the results when calculating the children.
class Solution {
public:
unordered_map<TreeNode* , int> umap;
int rob(TreeNode* root) {
if (root == NULL) return 0;
if (root->left == NULL && root->right == NULL) return root->val;
if (umap[root]) return umap[root];
// Rob the parent node
int val1 = root->val;
if (root->left) val1 += rob(root->left->left) + rob(root->left->right);
if (root->right) val1 += rob(root->right->left) + rob(root->right->right);
// Do not rob the parent node
int val2 = rob(root->left) + rob(root->right);
umap[root] = max(val1, val2);
return max(val1, val2);
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
- Time Complexity: O(n)
- Space Complexity: O(log n), considering the recursive system stack space
# Dynamic Programming
In the two methods above, we haven't recorded the maximum amount of money a node can get by robbing or not robbing, instead we calculate it in real-time.
Dynamic programming, however, means using a state transition container to record the state changes, and here we can use an array of size two to record the most money obtained by robbing or not robbing the current node.
This question is like an introduction to tree DP because the state transition occurs on the tree. When we talk about recursion in binary trees, we often use the three-step recursive approach, which I will use here combined with the five-step dynamic programming approach to explain this problem.
- Determine the parameters and return value of the recursive function
Here, we need to get the maximum money amount for robbing and not robbing a node, so the return value is an array of length 2.
The parameter is the current node, as shown in the following code:
vector<int> robTree(TreeNode* cur) {
Actually, this return array is the dp array.
So, the dp array (dp table) and the meaning of the index: index 0 records the maximum amount of money obtained by not robbing the node, and index 1 records the maximum amount obtained by robbing the node.
So in this case, the dp array is an array of length 2!
Some might wonder how an array of length 2 can mark the status of each node in the tree?
Remember that in the recursion process, the system stack will save the recursive parameters for each layer.
If you still don't understand, keep reading, and you'll get it when you see the code.
- Determine termination conditions
While traversing, if an empty node is encountered, it is apparent that both robbing and not robbing result in 0, so it returns:
if (cur == NULL) return vector<int>{0, 0};
This effectively initializes the dp array.
- Determine traversal order
First, it is essential to use post-order traversal since we need the return value of the recursive functions to compute the next steps.
Get the amount of money obtained by robbing and not robbing the left node through recursion.
Get the amount by robbing and not robbing the right node through recursion.
Code is as follows:
// index 0: not robbing, index 1: robbing
vector<int> left = robTree(cur->left); // left
vector<int> right = robTree(cur->right); // right
// root
2
3
4
- Determine the logic of a single-layer recursion
If the current node is robbed, then the left and right children node cannot be robbed, so val1 = cur->val + left[0] + right[0]; (refer to dp array's definition).
If not robbing the current node, then the left and right children node may or may not be robbed, whichever is maximum. Thus: val2 = max(left[0], left[1]) + max(right[0], right[1]).
Finally, the node's status after these evaluations is {val2, val1}; i.e., {maximum money obtained without robbing the node, maximum money obtained robbing the node}.
Code is as follows:
vector<int> left = robTree(cur->left); // left
vector<int> right = robTree(cur->right); // right
// Rob cur
int val1 = cur->val + left[0] + right[0];
// Not Rob cur
int val2 = max(left[0], left[1]) + max(right[0], right[1]);
return {val2, val1};
2
3
4
5
6
7
8
- Example of deriving the dp array
Using example 1, dp array states as follows (remember to use post-order traversal):
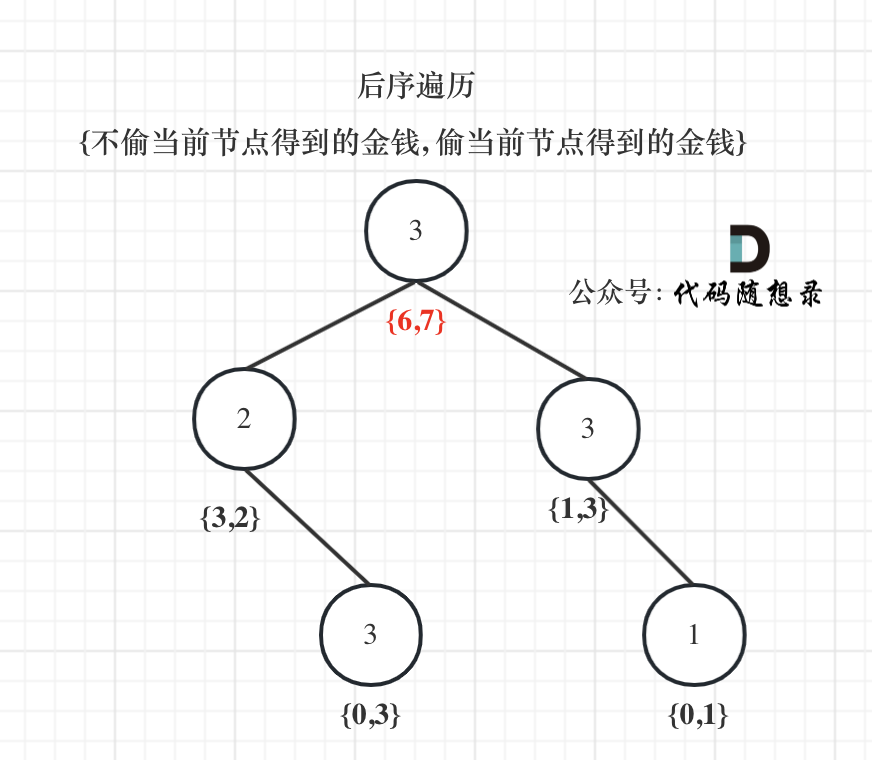
Finally, the root node is the maximum of index 0 and index 1, which is the maximum amount of money that can be robbed.
The recursive three-step approach combined with dynamic programming's five-step analysis is complete, C++ code is as follows:
class Solution {
public:
int rob(TreeNode* root) {
vector<int> result = robTree(root);
return max(result[0], result[1]);
}
// Array of length 2: 0: not robbing, 1: robbing
vector<int> robTree(TreeNode* cur) {
if (cur == NULL) return vector<int>{0, 0};
vector<int> left = robTree(cur->left);
vector<int> right = robTree(cur->right);
// Rob cur, then cannot rob left and right nodes.
int val1 = cur->val + left[0] + right[0];
// Not rob cur, can rob or not rob left and right nodes, take the larger situation
int val2 = max(left[0], left[1]) + max(right[0], right[1]);
return {val2, val1};
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
- Time Complexity: O(n), each node is visited only once
- Space Complexity: O(log n), considering the recursive system stack space
# Summary
This problem is an introductory example of tree DP. Through this problem, you should understand that tree DP is about deducing the recursive formula on a tree.
Tree DP is not that mysterious!
It's simply that we're used to deducing formulas on one-dimensional or two-dimensional arrays, and switching to trees requires a sufficient understanding of tree traversal!
Do you remember the problem discussed in the Greedy Algorithms section Greedy Algorithm: Binary Tree Cameras (opens new window)? It's an example of greedy algorithms applied on trees. I can also name this algorithm as Tree Greedy.
The term "Tree Greedy" is born, from "代码随想录".
# Other Language Versions
# Java
class Solution {
// 1. Recursive burglary that times out
public int rob(TreeNode root) {
if (root == null)
return 0;
int money = root.val;
if (root.left != null) {
money += rob(root.left.left) + rob(root.left.right);
}
if (root.right != null) {
money += rob(root.right.left) + rob(root.right.right);
}
return Math.max(money, rob(root.left) + rob(root.right));
}
// 2. Recursive burglary with state recording
// Execution time: 3 ms, beating 56.24% of users in Java submissions
public int rob1(TreeNode root) {
Map<TreeNode, Integer> memo = new HashMap<>();
return robAction(root, memo);
}
int robAction(TreeNode root, Map<TreeNode, Integer> memo) {
if (root == null)
return 0;
if (memo.containsKey(root))
return memo.get(root);
int money = root.val;
if (root.left != null) {
money += robAction(root.left.left, memo) + robAction(root.left.right, memo);
}
if (root.right != null) {
money += robAction(root.right.left, memo) + robAction(root.right.right, memo);
}
int res = Math.max(money, robAction(root.left, memo) + robAction(root.right, memo));
memo.put(root, res);
return res;
}
// 3. State-marked recursion
// Execution time: 0 ms, beating 100% of users in Java submissions
// If not robbing: Max(not robbing left child, robbing left child) + Max(not robbing right child, robbing right child)
// root[0] = Math.max(rob(root.left)[0], rob(root.left)[1]) +
// Math.max(rob(root.right)[0], rob(root.right)[1])
// If robbing: Not robbing left child + Not robbing right child + robbing current node
// root[1] = rob(root.left)[0] + rob(root.right)[0] + root.val;
public int rob3(TreeNode root) {
int[] res = robAction1(root);
return Math.max(res[0], res[1]);
}
int[] robAction1(TreeNode root) {
int res[] = new int[2];
if (root == null)
return res;
int[] left = robAction1(root.left);
int[] right = robAction1(root.right);
res[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
res[1] = root.val + left[0] + right[0];
return res;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
# Python
Brute Force Recursive
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rob(self, root: TreeNode) -> int:
if root is None:
return 0
if root.left is None and root.right is None:
return root.val
# Rob the parent node
val1 = root.val
if root.left:
val1 += self.rob(root.left.left) + self.rob(root.left.right)
if root.right:
val1 += self.rob(root.right.left) + self.rob(root.right.right)
# Do not rob the parent node
val2 = self.rob(root.left) + self.rob(root.right)
return max(val1, val2)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Memoized Recursion
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
memory = {}
def rob(self, root: TreeNode) -> int:
if root is None:
return 0
if root.left is None and root.right is None:
return root.val
if self.memory.get(root) is not None:
return self.memory[root]
# Rob the parent node
val1 = root.val
if root.left:
val1 += self.rob(root.left.left) + self.rob(root.left.right)
if root.right:
val1 += self.rob(root.right.left) + self.rob(root.right.right)
# Do not rob the parent node
val2 = self.rob(root.left) + self.rob(root.right)
self.memory[root] = max(val1, val2)
return max(val1, val2)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
Dynamic Programming
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def rob(self, root: Optional[TreeNode]) -> int:
# dp array (dp table) and the meaning of the index:
# 1. Index 0 records the maximum amount of money obtained by **not robbing the node**
# 2. Index 1 records the maximum amount of money obtained by **robbing the node**
dp = self.traversal(root)
return max(dp)
# Use post-order traversal, because the return values of the recursive functions are needed for subsequent calculations
def traversal(self, node):
# Termination condition of recursion
if not node:
return (0, 0)
left = self.traversal(node.left)
right = self.traversal(node.right)
# Not rob the current node, rob the child nodes
val_0 = max(left[0], left[1]) + max(right[0], right[1])
# Rob the current node, do not rob the child nodes
val_1 = node.val + left[0] + right[0]
return (val_0, val_1)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# Go
Brute force recursive solution
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func rob(root *TreeNode) int {
if root == nil {
return 0
}
if root.Left == nil && root.Right == nil {
return root.Val
}
// Rob the parent node
val1 := root.Val
if root.Left != nil {
val1 += rob(root.Left.Left) + rob(root.Left.Right)
}
if root.Right != nil {
val1 += rob(root.Right.Left) + rob(root.Right.Right)
}
// Do not rob the parent node
val2 := rob(root.Left) + rob(root.Right)
return max(val1, val2)
}
func max(x, y int) int {
if x > y {
return x
}
return y
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
Memoized recursive solution
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
var umap = make(map[*TreeNode]int)
func rob(root *TreeNode) int {
if root == nil {
return 0
}
if root.Left == nil && root.Right == nil {
return root.Val
}
if val, ok := umap[root]; ok {
return val
}
// Rob the parent node
val1 := root.Val
if root.Left != nil {
val1 += rob(root.Left.Left) + rob(root.Left.Right)
}
if root.Right != nil {
val1 += rob(root.Right.Left) + rob(root.Right.Right)
}
// Do not rob the parent node
val2 := rob(root.Left) + rob(root.Right)
umap[root] = max(val1, val2)
return max(val1, val2)
}
func max(x, y int) int {
if x > y {
return x
}
return y
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
Dynamic programming
func rob(root *TreeNode) int {
res := robTree(root)
return slices.Max(res)
}
func robTree(cur *TreeNode) []int {
if cur == nil {
return []int{0, 0}
}
// Post-order traversal
left := robTree(cur.Left)
right := robTree(cur.Right)
// Consider robbing current house
robCur := cur.Val + left[0] + right[0]
// Consider not robbing current house
notRobCur := slices.Max(left) + slices.Max(right)
// Note the order: 0: not robbing, 1: robbing
return []int{notRobCur, robCur}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# JavaScript
Dynamic Programming
const rob = root => {
// Post-order traversal function
const postOrder = node => {
// Recursive base case
if (!node) return [0, 0];
// Traverse left subtree
const left = postOrder(node.left);
// Traverse right subtree
const right = postOrder(node.right);
// Do not rob current node, rob or do not rob child nodes, take maximum
const DoNot = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
// Rob current node, do not rob child nodes
const Do = node.val + left[0] + right[0];
// [DoNot, Do]
return [DoNot, Do];
};
const res = postOrder(root);
// Return maximum value
return Math.max(...res);
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# TypeScript
Memoized Post-order Traversal
const memory: Map<TreeNode, number> = new Map();
function rob(root: TreeNode | null): number {
if (root === null) return 0;
if (memory.has(root)) return memory.get(root);
// Do not rob current node
const res1: number = rob(root.left) + rob(root.right);
// Rob current node
let res2: number = root.val;
if (root.left !== null) res2 += rob(root.left.left) + rob(root.left.right);
if (root.right !== null) res2 += rob(root.right.left) + rob(root.right.right);
const res: number = Math.max(res1, res2);
memory.set(root, res);
return res;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
State-marked Post-order Traversal
function rob(root: TreeNode | null): number {
return Math.max(...robNode(root));
};
// [0]-Do not rob current node, [1]-Rob current node
type MaxValueArr = [number, number];
function robNode(node: TreeNode | null): MaxValueArr {
if (node === null) return [0, 0];
const leftArr: MaxValueArr = robNode(node.left);
const rightArr: MaxValueArr = robNode(node.right);
// Do not rob
const val1: number = Math.max(leftArr[0], leftArr[1]) +
Math.max(rightArr[0], rightArr[1]);
// Rob
const val2: number = leftArr[0] + rightArr[0] + node.val;
return [val1, val2];
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# C
int *robTree(struct TreeNode *node) {
int* amounts = (int*) malloc(sizeof(int) * 2);
memset(amounts, 0, sizeof(int) * 2);
if(node == NULL){
return amounts;
}
int * left = robTree(node->left);
int * right = robTree(node->right);
// Rob current node
amounts[1] = node->val + left[0] + right[0];
// Do not rob current node
amounts[0] = max(left[0], left[1]) + max(right[0], right[1]);
return amounts;
}
int rob(struct TreeNode* root) {
int * dp = robTree(root);
// 0 represents not robbing the current node to get the maximum, 1 represents robbing the current node to get the maximum
return max(dp[0], dp[1]);
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# Rust
Dynamic Programming:
use std::cell::RefCell;
use std::rc::Rc;
impl Solution {
pub fn rob(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
let (v1, v2) = Self::rob_tree(&root);
v1.max(v2)
}
pub fn rob_tree(cur: &Option<Rc<RefCell<TreeNode>>>) -> (i32, i32) {
match cur {
None => (0, 0),
Some(node) => {
let left = Self::rob_tree(&node.borrow_mut().left);
let right = Self::rob_tree(&node.borrow_mut().right);
(
left.0.max(left.1) + right.0.max(right.1), // Rob left and right child
node.borrow().val + left.0 + right.0, // Rob parent
)
}
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
