# 62. Unique Paths
Link to LeetCode problem (opens new window)
A robot is located at the top-left corner of an m x n grid (marked as "Start" in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked as "Finish" in the diagram below).
How many possible unique paths are there?
Example 1:

- Input: m = 3, n = 7
- Output: 28
Example 2:
- Input: m = 2, n = 3
- Output: 3
Explanation: Starting from the top-left corner, there are a total of 3 ways to reach the bottom-right corner.
- Right -> Right -> Down
- Right -> Down -> Right
- Down -> Right -> Right
Example 3:
- Input: m = 7, n = 3
- Output: 28
Example 4:
- Input: m = 3, n = 3
- Output: 6
Constraints:
- 1 <= m, n <= 100
- The answer is guaranteed to be less than or equal to 2 * 10^9
# Approach
# Depth-First Search (DFS)
At first glance, a straightforward approach to solve this problem is to use depth-first search (DFS) from graph theory to enumerate all possible paths.
Since the robot can only move either down or right, the path it takes can actually be thought of as forming a binary tree, where each leaf node represents a potential path to the target.
For example:
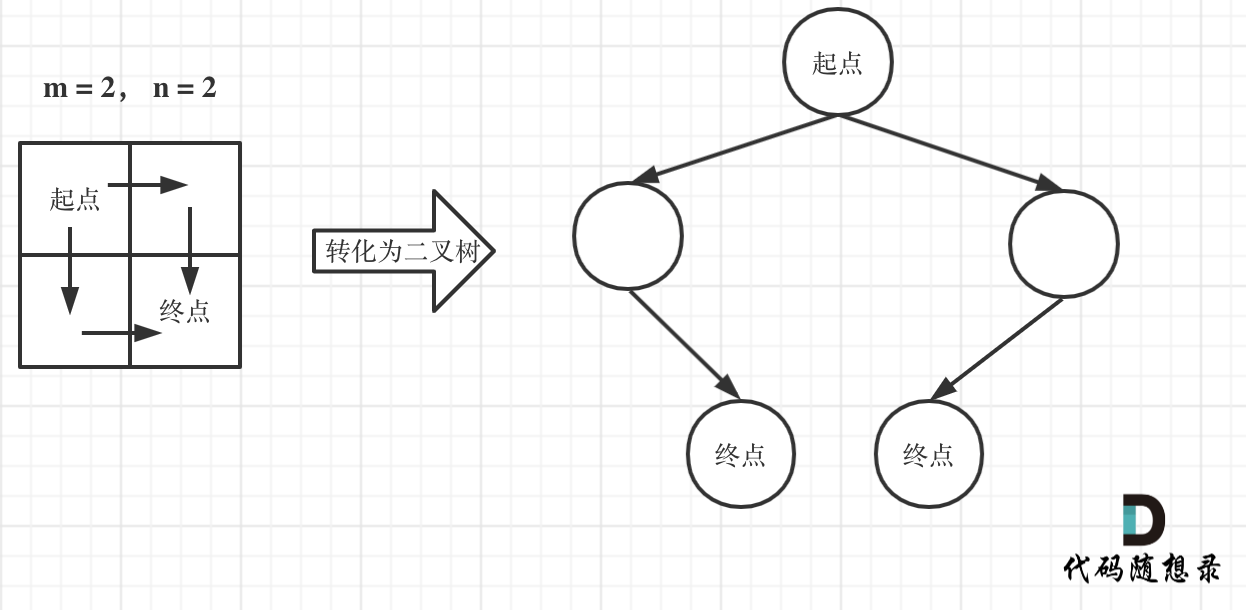
In this instance, the problem can be transformed into finding the number of leaf nodes in the binary tree. The code is as follows:
class Solution {
private:
int dfs(int i, int j, int m, int n) {
if (i > m || j > n) return 0; // Out of bounds
if (i == m && j == n) return 1; // Found a valid path, corresponds to a leaf node
return dfs(i + 1, j, m, n) + dfs(i, j + 1, m, n);
}
public:
int uniquePaths(int m, int n) {
return dfs(1, 1, m, n);
}
};
2
3
4
5
6
7
8
9
10
11
12
If you run this code, you'll notice it leads to a timeout!
To analyze the time complexity, this DFS algorithm essentially needs to traverse the entire binary tree.
The depth of this tree is m+n-1 (considering depth starting from 1).
The number of nodes in the binary tree would be 2^(m + n - 1) - 1. This can be understood as the DFS algorithm traversing an almost complete binary tree.
Thus, the time complexity of the above DFS code is O(2^(m + n - 1) - 1), which is an exponential time complexity, exceptionally high.
# Dynamic Programming
The robot starts from position (0, 0) and aims to reach the endpoint (m - 1, n - 1).
Let's analyze using the dynamic programming five-step approach:
- Define the dp array and its index meaning.
dp[i][j]: Represents the number of different paths from (0, 0) to (i, j).
- Determine the recursive formula.
To find dp[i][j], it can only be derived from two directions, i.e., dp[i - 1][j] and dp[i][j - 1].
Recall that dp[i - 1][j] represents the number of paths from (0, 0) to (i - 1, j) and dp[i][j - 1] similarly.
Thus, naturally, dp[i][j] = dp[i - 1][j] + dp[i][j - 1], as dp[i][j] can only come from these two directions.
- Initialize the dp array.
How to initialize? Initially, dp[i][0] should all be 1, because there's only one path from (0, 0) to (i, 0), and the same logic applies to dp[0][j].
The initialization code is:
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;
2
- Determine the iteration order.
Here, look at the recursive formula dp[i][j] = dp[i - 1][j] + dp[i][j - 1], where dp[i][j] is derived from its top and left side, hence iterating layer by layer from left to right will suffice.
This ensures dp[i][j] has calculated values for dp[i - 1][j] and dp[i][j - 1].
- Example to infer the dp array.
As illustrated below:
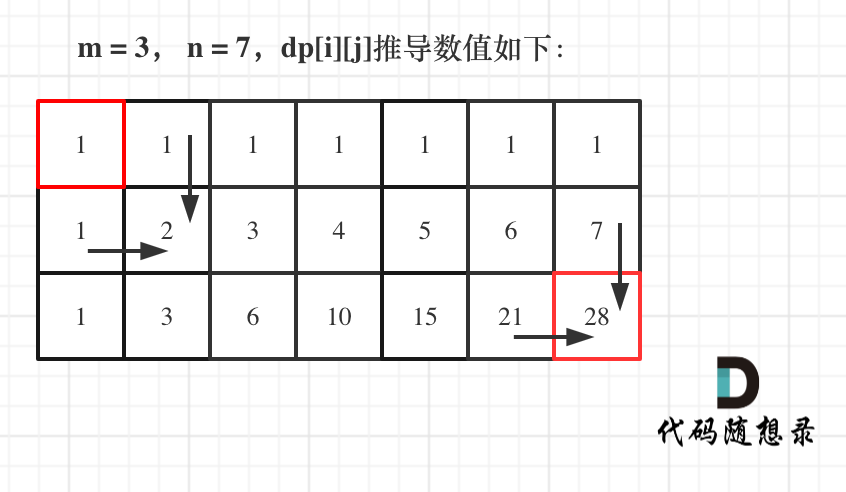
Here's the complete analysis and the C++ code:
class Solution {
public:
int uniquePaths(int m, int n) {
vector<vector<int>> dp(m, vector<int>(n, 0));
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
- Time Complexity: O(m × n)
- Space Complexity: O(m × n)
Actually, this can be optimized using a one-dimensional array (or rolling array), but a 2D array is easier to understand. For those who have understood the 2D array approach, consider looking into the 1D approach. The C++ code is as follows:
class Solution {
public:
int uniquePaths(int m, int n) {
vector<int> dp(n);
for (int i = 0; i < n; i++) dp[i] = 1;
for (int j = 1; j < m; j++) {
for (int i = 1; i < n; i++) {
dp[i] += dp[i - 1];
}
}
return dp[n - 1];
}
};
2
3
4
5
6
7
8
9
10
11
12
13
- Time Complexity: O(m × n)
- Space Complexity: O(n)
# Combinatorial Approach
In this grid, any complete path for m and n must consist of exactly m + n - 2 steps.
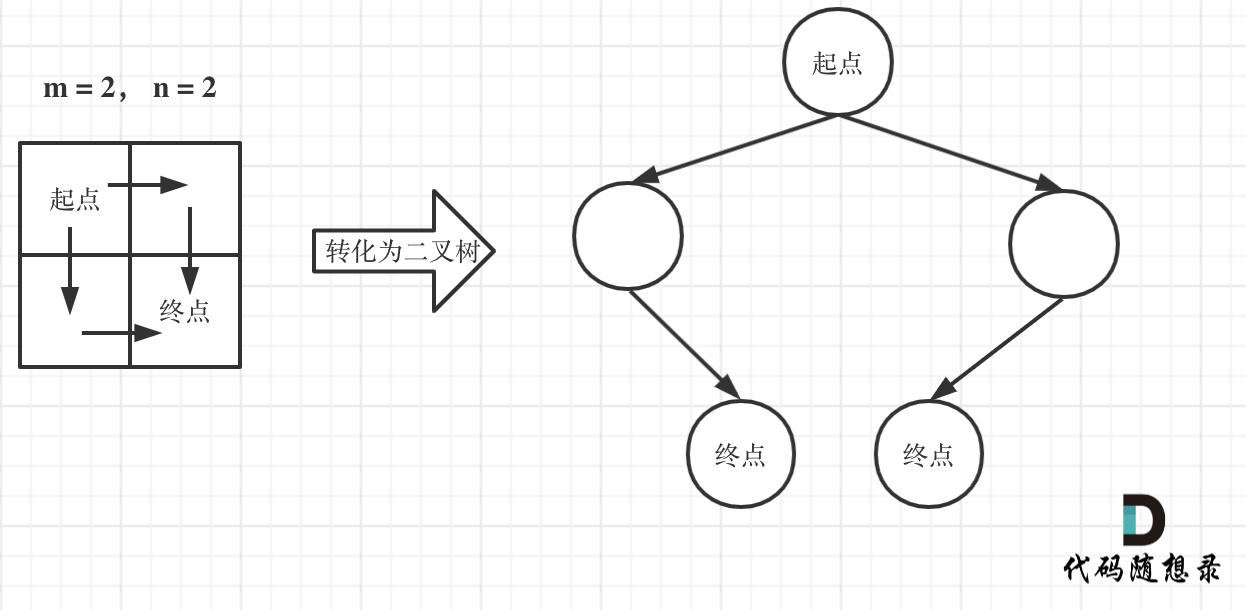
Among these m + n - 2 steps, there must be exactly m - 1 steps that move downward, no matter in which order they occur.
So how many ways are there? It can be transformed into selecting m - 1 steps from m + n - 2 steps.
Thus, it's a combinatorial problem.
The solution is depicted as follows:
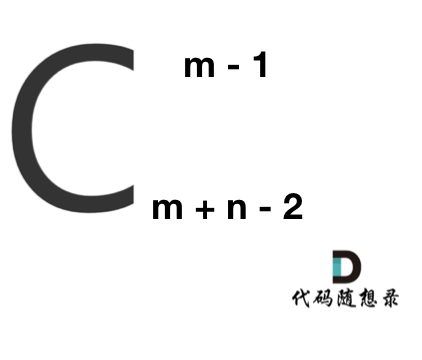
When calculating combinations, be cautious of overflow from multiplying two integers! Hence, do not calculate the numerator and denominator separately before performing division.
For example, the following code is invalid.
class Solution {
public:
int uniquePaths(int m, int n) {
int numerator = 1, denominator = 1;
int count = m - 1;
int t = m + n - 2;
while (count--) numerator *= (t--); // Calculating the numerator directly causes overflow
for (int i = 1; i <= m - 1; i++) denominator *= i; // Calculating the denominator
return numerator / denominator;
}
};
2
3
4
5
6
7
8
9
10
11
You need to continuously divide the numerator by the denominator while calculating it, code as follows:
class Solution {
public:
int uniquePaths(int m, int n) {
long long numerator = 1; // Numerator
int denominator = m - 1; // Denominator
int count = m - 1;
int t = m + n - 2;
while (count--) {
numerator *= (t--);
while (denominator != 0 && numerator % denominator == 0) {
numerator /= denominator;
denominator--;
}
}
return numerator;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
- Time Complexity: O(m)
- Space Complexity: O(1)
The code for calculating a combination problem is not easy, especially handling overflow!
# Summary
In this article, three solutions are provided: DFS, dynamic programming, and combinatorial.
DFS clearly results in a timeout. We also analyzed the time complexity of DFS to understand why it times out.
Then, we presented the DP solution using a structured five-step approach, emphasizing the importance of correct initialization.
# Other Language Versions
# Java
/**
* 1. Determine the dp array index meaning: dp[i][j] is the count of unique paths to each coordinate.
* 2. Recurrence relation: dp[i][j] = dp[i-1][j] + dp[i][j-1]
* 3. Initialization: dp[i][0]=1, dp[0][i]=1; initialize the first row/column.
* 4. Iteration order: Line by line traversal
* 5. Deduct the result .........
*
* @param m
* @param n
* @return
*/
public static int uniquePaths(int m, int n) {
int[][] dp = new int[m][n];
// Initialization
for (int i = 0; i < m; i++) {
dp[i][0] = 1;
}
for (int i = 0; i < n; i++) {
dp[0][i] = 1;
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
return dp[m-1][n-1];
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
State Compression
class Solution {
public int uniquePaths(int m, int n) {
// In a 2D dp array, the current value depends only on the top and left values, so it can be compressed into a 1D array.
int[] dp = new int[n];
// Initialization: the first row can only be reached from the left, so there is only one path.
Arrays.fill(dp, 1);
for (int i = 1; i < m; i ++) {
// The first column also has only one path, so start from the second column.
for (int j = 1; j < n; j ++) {
dp[j] += dp[j - 1]; // dp[j] = dp[j] (from above) + dp[j - 1] (from left)
}
}
return dp[n - 1];
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# Python
Recursion
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
if m == 1 or n == 1:
return 1
return self.uniquePaths(m - 1, n) + self.uniquePaths(m, n - 1)
2
3
4
5
Dynamic Programming (Version 1)
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
# Create a 2D list for storing unique path counts
dp = [[0] * n for _ in range(m)]
# Set up base cases for the first row and first column
for i in range(m):
dp[i][0] = 1
for j in range(n):
dp[0][j] = 1
# Calculate the number of unique paths for each cell
for i in range(1, m):
for j in range(1, n):
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
# Return the number of unique paths for the bottom-right cell
return dp[m - 1][n - 1]
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Dynamic Programming (Version 2)
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
# Create a 1D list for storing unique path counts per column
dp = [1] * n
# Calculate the number of unique paths for each cell
for j in range(1, m):
for i in range(1, n):
dp[i] += dp[i - 1]
# Return the number of unique paths for the bottom-right cell
return dp[n - 1]
2
3
4
5
6
7
8
9
10
11
12
Combinatorial
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
numerator = 1 # Numerator
denominator = m - 1 # Denominator
count = m - 1 # Counter representing the number of remaining factorial products needed
t = m + n - 2 # Initial factorial product
while count > 0:
numerator *= t # Calculate the numerator part of the factorial product
t -= 1 # Decrement the factorial product
while denominator != 0 and numerator % denominator == 0:
numerator //= denominator # Simplify the numerator
denominator -= 1 # Decrement the denominator
count -= 1 # Decrease counter to continue calculating the next product
return numerator # Return the final unique path count
2
3
4
5
6
7
8
9
10
11
12
13
14
# Go
Dynamic Programming
func uniquePaths(m int, n int) int {
dp := make([][]int, m)
for i := range dp {
dp[i] = make([]int, n)
dp[i][0] = 1
}
for j := 0; j < n; j++ {
dp[0][j] = 1
}
for i := 1; i < m; i++ {
for j := 1; j < n; j++ {
dp[i][j] = dp[i-1][j] + dp[i][j-1]
}
}
return dp[m-1][n-1]
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Combinatorial Approach
func uniquePaths(m int, n int) int {
numerator := 1
denominator := m - 1
count := m - 1
t := m + n - 2
for count > 0 {
numerator *= t
t--
for denominator != 0 && numerator % denominator == 0 {
numerator /= denominator
denominator--
}
count--
}
return numerator
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# JavaScript
var uniquePaths = function(m, n) {
const dp = Array(m).fill().map(item => Array(n))
for (let i = 0; i < m; ++i) {
dp[i][0] = 1
}
for (let i = 0; i < n; ++i) {
dp[0][i] = 1
}
for (let i = 1; i < m; ++i) {
for (let j = 1; j < n; ++j) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
}
}
return dp[m - 1][n - 1]
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Version 2: Directly initialize dp values to 1
/**
* @param {number} m
* @param {number} n
* @return {number}
*/
var uniquePaths = function(m, n) {
let dp = new Array(m).fill(1).map(() => new Array(n).fill(1));
// dp[i][j] indicates the number of paths to reach the point (i, j)
for (let i = 1; i < m; i++) {
for (let j = 1; j < n; j++) {
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
return dp[m-1][n-1];
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# TypeScript
function uniquePaths(m: number, n: number): number {
/**
dp[i][j]: The number of paths to reach (i, j)
dp[0][*]: 1;
dp[*][0]: 1;
...
dp[i][j]: dp[i - 1][j] + dp[i][j - 1];
*/
const dp: number[][] = new Array(m).fill(0).map(_ => []);
for (let i = 0; i < m; i++) {
dp[i][0] = 1;
}
for (let i = 0; i < n; i++) {
dp[0][i] = 1;
}
for (let i = 1; i < m; i++) {
for (let j = 1; j < n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# Rust
impl Solution {
pub fn unique_paths(m: i32, n: i32) -> i32 {
let (m, n) = (m as usize, n as usize);
let mut dp = vec![vec![1; n]; m];
for i in 1..m {
for j in 1..n {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
dp[m - 1][n - 1]
}
}
2
3
4
5
6
7
8
9
10
11
12
# C
// Initialize the dp array
int **initDP(int m, int n) {
// Dynamically allocate the dp array
int **dp = (int**)malloc(sizeof(int *) * m);
int i, j;
for(i = 0; i < m; ++i) {
dp[i] = (int *)malloc(sizeof(int) * n);
}
// From (0, 0) to (i, 0), there's only one path, hence dp[i][0] is 1, the same applies to dp[0][j]
for(i = 0; i < m; ++i)
dp[i][0] = 1;
for(j = 0; j < n; ++j)
dp[0][j] = 1;
return dp;
}
int uniquePaths(int m, int n){
// dp array: dp[i][j] represents the number of paths from dp[0][0] to dp[i][j]
int **dp = initDP(m, n);
int i, j;
// To reach dp[i][j], one can only start from dp[i-1][j] or dp[i][j-1]
// dp[i][j] = dp[i-1][j] + dp[i][j-1]
for(i = 1; i < m; ++i) {
for(j = 1; j < n; ++j) {
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
int result = dp[m-1][n-1];
free(dp);
return result;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
Rolling Array Solution:
int uniquePaths(int m, int n){
int i, j;
// Initialize dp array
int *dp = (int*)malloc(sizeof(int) * n);
for (i = 0; i < n; ++i)
dp[i] = 1;
for (j = 1; j < m; ++j) {
for (i = 1; i < n; ++i) {
// dp[i] stands for dp[i-1][j] from the 2D dp solution; dp[i-1] stands for dp[i][j-1]
dp[i] += dp[i - 1];
}
}
return dp[n - 1];
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# Scala
object Solution {
def uniquePaths(m: Int, n: Int): Int = {
var dp = Array.ofDim[Int](m, n)
for (i <- 0 until m) dp(i)(0) = 1
for (j <- 1 until n) dp(0)(j) = 1
for (i <- 1 until m; j <- 1 until n) {
dp(i)(j) = dp(i - 1)(j) + dp(i)(j - 1)
}
dp(m - 1)(n - 1)
}
}
2
3
4
5
6
7
8
9
10
11
# C#
// 2D array
public class Solution
{
public int UniquePaths(int m, int n)
{
int[,] dp = new int[m, n];
for (int i = 0; i < m; i++) dp[i, 0] = 1;
for (int j = 0; j < n; j++) dp[0, j] = 1;
for (int i = 1; i < m; i++)
{
for (int j = 1; j < n; j++)
{
dp[i, j] = dp[i - 1, j] + dp[i, j - 1];
}
}
return dp[m - 1, n - 1];
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// 1D array
public class Solution
{
public int UniquePaths(int m, int n)
{
int[] dp = new int[n];
for (int i = 0; i < n; i++)
dp[i] = 1;
for (int i = 1; i < m; i++)
for (int j = 1; j < n; j++)
dp[j] += dp[j - 1];
return dp[n - 1];
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
