# 343. Integer Break

LeetCode Problem Link (opens new window)

Given a positive integer n, break it into the sum of at least two positive integers and maximize the product of those integers. Return the maximum product you can get.

Example 1:

Input: 2
Output: 1
Explanation: 2 = 1 + 1, 1 × 1 = 1.

Example 2:

Input: 10
Output: 36
Explanation: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36.
Note: You may assume that n is not less than 2 and not greater than 58.

# Approach

When encountering this problem, we think about whether to break it into two, three, or four parts...

Let's explore how to use dynamic programming to solve it.

# Dynamic Programming

Let's analyze using the five steps of dynamic programming:

Define the dp array (dp table) and the meaning of its indices

dp[i]: The maximum product obtained by breaking the number i.

The definition of dp[i] will be carried through the entire solution process. Whenever something is unclear, consider what dp[i] actually represents!
Determine the recursion formula

How is the maximum product dp[i] obtained?

We can iterate over j from 1, with two ways to obtain dp[i].

One way is direct multiplication: ( j \times (i-j) ).

The other is by breaking down ((i-j)): ( j \times dp[i-j] ). Think of the definition of the dp array if this is unclear.

A common question might be: Why not further split j?

Since we start iterating j from 1, splitting j has already been covered in the iterations. So iterating from 1 to j, we compare ((i-j) \times j) and ( dp[i-j] \times j) to get the maximum. The recursion formula: dp[i] = max(dp[i], max((i-j) * j, dp[i-j] * j));

We can also interpret this: ( j \times (i-j) ) simply breaks the integer into two numbers multiplying, and ( j \times dp[i-j] ) breaks it into two or more parts.

Using dp[i-j] * dp[j] implicitly means breaking the number into four or more parts.

So the formula is: dp[i] = max({dp[i], (i-j) * j, dp[i-j] * j});

Then why still compare with dp[i]?

Because in deriving the formula, each calculation of dp[i] takes the maximum value.
Initialize dp

Some might wonder how to initialize dp[0] and dp[1]?

Some discussions set dp[0] = 1 and dp[1] = 1, but explanations can be inadequate, mainly because such initialization could solve the problem.

Strictly according to dp[i]'s definition, dp[0] and dp[1] shouldn't be initialized; they hold no meaningful values.

What is the maximum product when breaking 0 or 1?

It is unsolvable.

Here we only initialize dp[2] = 1. According to dp[i]'s definition, breaking the number 2, the maximum product is 1, which is indisputable!
Determine the iteration order

Consider the recursion formula: dp[i] = max(dp[i], max((i-j) * j, dp[i-j] * j));

Since dp[i] depends on the state of dp[i-j], the iteration for i should definitely go from front to back, starting with dp[i-j] and then having dp[i].

Thus the iteration order is:
```
for (int i = 3; i <= n ; i++) {
    for (int j = 1; j < i - 1; j++) {
        dp[i] = max(dp[i], max((i-j) * j, dp[i-j] * j));
    }
}
```
1
2
3
4
5
Note: Iterate j starting from 1. Starting from 0 doesn't make sense since breaking a number with a 0 to get the maximum product holds no meaning.

j's end condition could very well be j < i but stopping at j < i - 1 is slightly more efficient, saving one step; for instance, preemptively handling when j = i - 1, has already been considered j = 1.

Regarding where to begin i from 3, this allows dp[i-j] to utilize correctly initialized values as dp[2].

Further optimization could be:
```
for (int i = 3; i <= n ; i++) {
    for (int j = 1; j <= i / 2; j++) {
        dp[i] = max(dp[i], max((i-j) * j, dp[i-j] * j));
    }
}
```
1
2
3
4
5
Given breaking a number n to maximize product, always breaks into m similar parts for the largest product.

Example: breaking 6 into 3 * 3 or breaking 10 into 3 * 3 * 4. For 100 too, it’s the same concept of breaking into m similar parts for maximum product.

Though we don't know the exact value of m, we know it’s at least 2. So the worst is splitting into two similar parts, potentially the largest value.

Thus, j only iterates until ( n/2 ); after that, it’s not the maximum value. Exploring the proof that “breaking a number n maximizes when breaking into m similar parts” is an interesting research area left for the curious.

Example of deriving the dp array

When n is 10, the values in the dp array are as follows:

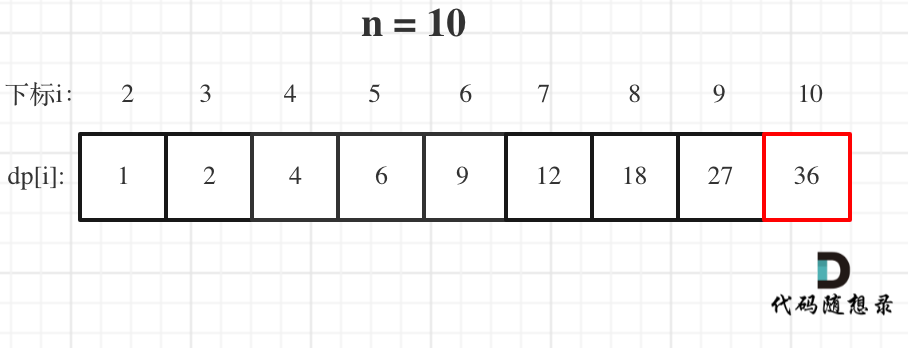
343. Integer Break

After analyzing the dynamic programming five steps, the C++ code is as follows:

class Solution {
public:
    int integerBreak(int n) {
        vector<int> dp(n + 1);
        dp[2] = 1;
        for (int i = 3; i <= n ; i++) {
            for (int j = 1; j <= i / 2; j++) {
                dp[i] = max(dp[i], max((i-j) * j, dp[i-j] * j));
            }
        }
        return dp[n];
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13

Time Complexity: O(n^2)
Space Complexity: O(n)

# Greedy

This problem can also be solved greedily by splitting as many 3s as possible. If the remainder is 4, keep it and multiply, which requires mathematical proof for validity!

I haven't provided a proof, but utilized the conclusion. For those curious, further study on mathematical justification is encouraged.

Here's my C++ code:

class Solution {
public:
    int integerBreak(int n) {
        if (n == 2) return 1;
        if (n == 3) return 2;
        if (n == 4) return 4;
        int result = 1;
        while (n > 4) {
            result *= 3;
            n -= 3;
        }
        result *= n;
        return result;
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

Time Complexity: O(n)
Space Complexity: O(1)

# Conclusion

Master the dynamic programming approach for this problem. Although the greedy solution is simple, it requires mathematical proof; if one can justify it, that's acceptable.

My initial attempt at this problem was such:

class Solution {
public:
    int integerBreak(int n) {
        if (n <= 3) return 1 * (n - 1);
        vector<int> dp(n + 1, 0);
        dp[1] = 1;
        dp[2] = 2;
        dp[3] = 3;
        for (int i = 4; i <= n ; i++) {
            for (int j = 1; j <= i / 2; j++) {
                dp[i] = max(dp[i], dp[i - j] * dp[j]);
            }
        }
        return dp[n];
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

This code can also be accepted!

The recursion formula appears logical, with dp[i] equal to the maximum product from splitting i-j multiplied by splitting j. It seems legitimate!

However, upon explaining initialization, contradictions arise: why must dp[1] be 1, and according to dp[i] definition, dp[2] shouldn’t be 2.

Yet if the recursion formula is dp[i] = max(dp[i], dp[i-j] * dp[j]);, it forces such initialization. The formula is logical, but the initialization contradicts itself.

Though the initial position has a check if (n <= 3) return 1 * (n - 1);, ensuring correct results for n <= 3, the code later assigns dp[1] value 1 and dp[2] value 2, which contradicts dp[i]'s own definition!

I highlight this example to emphasize the importance of precision; though the above code can be AC, and superficially seems right, the correct result just happens by chance.

# Other Language Versions

# Java

class Solution {
    public int integerBreak(int n) {
        int[] dp = new int[n+1]; // dp[i] is the maximum product after breaking integer i
        dp[2] = 1;
        for(int i = 3; i <= n; i++) {
            for(int j = 1; j <= i-j; j++) {
                // j <= i-j means within the range, no need to surpass it, no risking using dp[0] or dp[1]
                dp[i] = Math.max(dp[i], Math.max(j*(i-j), j*dp[i-j]));
                // j * (i - j) simply splits i into two numbers i, i-j, and then multiplies
                // j * dp[i - j] actually splits i into two or more numbers before multiplying.
            }
        }
        return dp[n];
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

Greedy

class Solution {
    public int integerBreak(int n) {
        if(n == 2) return 1;
        if(n == 3) return 2;
        int result = 1;
        while(n > 4) {
            n-=3;
            result *=3;
        }
        return result*n;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12

# Python

Dynamic Programming (Version 1)

class Solution:
         # Assume breaking integer i first results in j (1 <= j < i), hence two solutions:
        # 1) Break i into j and i-j, i-j not split further, product is j * (i-j)
        # 2) Break i into j and i-j, and further split i-j, product is j * dp[i-j]
    def integerBreak(self, n):
        dp = [0] * (n + 1)
        dp[2] = 1  # Initialize dp[2] as 1, as for n=2 there's only one split manner: 1+1=2, product is 1
       
        # Calculate from 3 through n
        for i in range(3, n + 1):
            # Traverse all possible split points
            for j in range(1, i // 2 + 1):

                # Calculate the product of split j and remaining (i-j), compare and take the bigger one
                
                dp[i] = max(dp[i], (i - j) * j, dp[i - j] * j)
        
        return dp[n]  # Return the final calculated result

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

Dynamic Programming (Version 2)

class Solution:
    def integerBreak(self, n):
        if n <= 3:
            return 1 * (n - 1)  # For n less than or equal to 3, return 1 * (n - 1)

        dp = [0] * (n + 1)  # Create an array of size n+1 to store maximum product results
        dp[1] = 1  # When n equals 1, the maximum product is 1
        dp[2] = 2  # When n equals 2, the maximum product is 2
        dp[3] = 3  # When n equals 3, the maximum product is 3

        # Calculate from 4 through n
        for i in range(4, n + 1):
            # Traverse all possible split points
            for j in range(1, i // 2 + 1):
                # Calculate the product of split j and remaining (i - j), compare and take the bigger one
                dp[i] = max(dp[i], dp[i - j] * dp[j])

        return dp[n]  # Return the maximum product result of integer split

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

Greedy

class Solution:
    def integerBreak(self, n):
        if n == 2:  # For n equals 2, only one split way: 1+1=2, product is 1
            return 1
        if n == 3:  # For n equals 3, only one split way: 2+1=3, product is 2
            return 2
        if n == 4:  # For n equals 4, two split ways: 2+2=4 and 1+1+1+1=4, product is 4
            return 4
        result = 1
        while n > 4:
            result *= 3  # Multiply by 3 each time, as 3’s product surpasses other numbers
            n -= 3  # Subtract 3 each time
        result *= n  # Multiply the remainder n by the final result
        return result

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

# Go

Dynamic Programming

func integerBreak(n int) int {
    /**
    Dynamic Programming Five Steps
    1. Define dp indices and their meaning
    2. Define the recursion formula
    3. Initialize dp
    4. Define the loop order
    5. Print dp
    **/
    dp := make([]int, n+1)
    dp[1] = 1
    dp[2] = 1
    for i := 3; i < n+1; i++ {
        for j := 1; j < i-1; j++ {
// i can be broken into i-j and j. To ensure the maximum, iterate through existing values for j and take the maximum of three: the previous dp[i], the original multiplication, or j multiplied by dp[i-j].
            dp[i] = max(dp[i], max(j*(i-j), j*dp[i-j]))
        }
    }
    return dp[n]
}
func max(a, b int) int{
    if a > b {
        return a
    }
    return b
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

Greedy

func integerBreak(n int) int {
    if n == 2 {
        return 1
    }
    if n == 3 {
        return 2
    }
    if n == 4 {
        return 4
    }
    result := 1
    for n > 4 {
        result *= 3
        n -= 3
    }
    result *= n
    return result
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

# JavaScript

var integerBreak = function(n) {
    let dp = new Array(n + 1).fill(0)
    dp[2] = 1

    for(let i = 3; i <= n; i++) {
        for(let j = 1; j <= i / 2; j++) {
            dp[i] = Math.max(dp[i], dp[i - j] * j, (i - j) * j)
        }
    }
    return dp[n]
};

1
2
3
4
5
6
7
8
9
10
11

# Rust

pub fn integer_break(n: i32) -> i32 {
    let n = n as usize;
    let mut dp = vec![0; n + 1];
    dp[2] = 1;
    for i in 3..=n {
        for j in 1..i-1 {
            dp[i] = dp[i].max((i - j) * j).max(dp[i - j] * j);
        }
    }
    dp[n] as i32
}

1
2
3
4
5
6
7
8
9
10
11

Greedy:

impl Solution {
    pub fn integer_break(mut n: i32) -> i32 {
        match n {
            2 => 1,
            3 => 2,
            4 => 4,
            5.. => {
                let mut res = 1;
                while n > 4 {
                    res *= 3;
                    n -= 3;
                }
                res * n
            }
            _ => panic!("Error"),
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

# TypeScript

function integerBreak(n: number): number {
    /**
        dp[i]: i corresponds to the maximum product
        dp[2]: 1;
        ...
        dp[i]: max(
            1 * dp[i - 1], 1 * (i - 1),
            2 * dp[i - 2], 2 * (i - 2),
            ..., (i - 2) * dp[2], (i - 2) * 2
        );
     */
    const dp: number[] = new Array(n + 1).fill(0);
    dp[2] = 1;
    for (let i = 3; i <= n; i++) {
        for (let j = 1; j <= i / 2; j++) {
            dp[i] = Math.max(dp[i], j * dp[i - j], j * (i - j));
        }
    }
    return dp[n];
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

# C

// Initialize DP array
int *initDP(int num) {
    int* dp = (int*)malloc(sizeof(int) * (num + 1));
    int i;
    for(i = 0; i < num + 1; ++i) {
        dp[i] = 0;
    }
    return dp;
}

// Get maximum of three numbers
int max(int num1, int num2, int num3) {
    int tempMax = num1 > num2 ? num1 : num2;
    return tempMax > num3 ? tempMax : num3;
}

int integerBreak(int n){
    int *dp = initDP(n);
    // Initialize dp[2] as 1
    dp[2] = 1;

    int i;
    for(i = 3; i <= n; ++i) {
        int j;
        for(j = 1; j < i - 1; ++j) {
            // Retrieve maximum of previous loop: dp[i], original multiplication, or j*dp[i-j].
            dp[i] = max(dp[i], j * (i - j), j * dp[i - j]);
        }
    }
    return dp[n];
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

# Scala

object Solution {
  def integerBreak(n: Int): Int = {
    var dp = new Array[Int](n + 1)
    dp(2) = 1
    for (i <- 3 to n) {
      for (j <- 1 until i - 1) {
        dp(i) = math.max(dp(i), math.max(j * (i - j), j * dp(i - j)))
      }
    }
    dp(n)
  }
}

1
2
3
4
5
6
7
8
9
10
11
12

# PHP

class Solution {

    /**
     * @param Integer $n
     * @return Integer
     */
    function integerBreak($n) {
        if($n == 0 || $n == 1) return 0;
        if($n == 2) return 1;

        $dp = [];
        $dp[0] = 0;
        $dp[1] = 0;
        $dp[2] = 1;
        for($i=3;$i<=$n;$i++){
            for($j = 1;$j <= $i/2; $j++){
                $dp[$i] = max(($i-$j)*$j, $dp[$i-$j]*$j, $dp[$i]);
            }
        }

        return $dp[$n];
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# C#

public class Solution
{
    public int IntegerBreak(int n)
    {
        int[] dp = new int[n + 1];
        dp[2] = 1;
        for (int i = 3; i <= n; i++)
        {
            for (int j = 1; j <= i / 2; j++)
            {
                dp[i] = Math.Max(dp[i],Math.Max(j*(i-j),j*dp[i-j]));
            }
        }
        return dp[n];
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

← 6. Unique Paths II 8. Unique Binary Search Trees →