# 123. Best Time to Buy and Sell Stock III
LeetCode Problem Link (opens new window)
Given an array, its i-th element represents the stock price on day i.
Design an algorithm to calculate the maximum profit you can achieve. You may complete at most two transactions.
Note: You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
Example 1:
Input: prices = [3,3,5,0,0,3,1,4]
Output: 6 Explanation: Buy on day 4 (stock price = 0) and sell on day 6 (stock price = 3), profit = 3-0 = 3. Then, buy on day 7 (stock price = 1) and sell on day 8 (stock price = 4), profit = 4-1 = 3.
Example 2:
Input: prices = [1,2,3,4,5]
Output: 4 Explanation: Buy on day 1 (stock price = 1) and sell on day 5 (stock price = 5), profit = 5-1 = 4. Note that you cannot buy on day 1, buy on day 2 and then sell them later, as you are engaging multiple transactions at the same time. You must sell your stocks before you buy again.
Example 3:
Input: prices = [7,6,4,3,1]
Output: 0 Explanation: In this case, no transaction is done, so the maximum profit is 0.
Example 4:
Input: prices = [1]
Output: 0
Constraints:
- 1 <= prices.length <= 10^5
- 0 <= prices[i] <= 10^5
# Solution
This problem is considerably more challenging compared to 0121.Best Time to Buy and Sell Stock (opens new window) and 0122.Best Time to Buy and Sell Stock II (opens new window).
The key to solving this problem is understanding that you can make at most two complete transactions, which implies you can complete zero, one, or two transactions.
Let’s break it down using the dynamic programming approach with five key steps:
- Define the DP array and its meaning
There are five states in a day:
- No operation (actually, we can omit this state).
- Hold stock for the first time.
- Do not hold stock for the first time.
- Hold stock for the second time.
- Do not hold stock for the second time.
In dp[i][j], i represents the i-th day, j is in the range [0 - 4] indicating the five states, and dp[i][j] represents the maximum cash available on day i for state j.
It's crucial to note: dp[i][1] represents holding the stock on day i, not necessarily buying it on that day, which is a common point of confusion.
For example, dp[i][1] does not mean you have to buy the stock on day i; it could have been bought on day i-1, and dp[i][1] merely extends this state of holding stock.
- Determine the recursive formula
To reach the state dp[i][1], there are two operations:
- Operation 1: Bought the stock on day i, so
dp[i][1] = dp[i-1][0] - prices[i]. - Operation 2: Did nothing on day i, extending a previously held state, so
dp[i][1] = dp[i-1][1].
The goal is to choose the max, so dp[i][1] = max(dp[i-1][0] - prices[i], dp[i-1][1]).
Similarly, for dp[i][2]:
- Operation 1: Sold the stock on day i, so
dp[i][2] = dp[i-1][1] + prices[i]. - Operation 2: Did nothing, so
dp[i][2] = dp[i-1][2].
Hence, dp[i][2] = max(dp[i-1][1] + prices[i], dp[i-1][2]).
The same logic applies to the remaining states:
dp[i][3] = max(dp[i-1][3], dp[i-1][2] - prices[i]);
dp[i][4] = max(dp[i-1][4], dp[i-1][3] + prices[i]);
- Initialization of the DP array
On the 0-th day, with no operation: dp[0][0] = 0;
On the 0-th day, the state of buying the first stock: dp[0][1] = -prices[0];
On the 0-th day, the state of selling stock for the first time: Though no buy action has been undertaken, it can be viewed as buying and selling on the same day, so dp[0][2] = 0;
For buying stock the second time on the 0-th day, it relies on the state of having previously sold once, essentially equivalent to having done one complete buy-sell cycle, leaving cash at dp[0][3] = -prices[0];
Similarly, the initialization for selling the second time: dp[0][4] = 0;
- Determine the traversal order
From the recursive formula, it's clear the traversal must be from past to present, as dp[i] relies on dp[i-1].
- Example for array
prices = [1,2,3,4,5]
Below is the DP array:
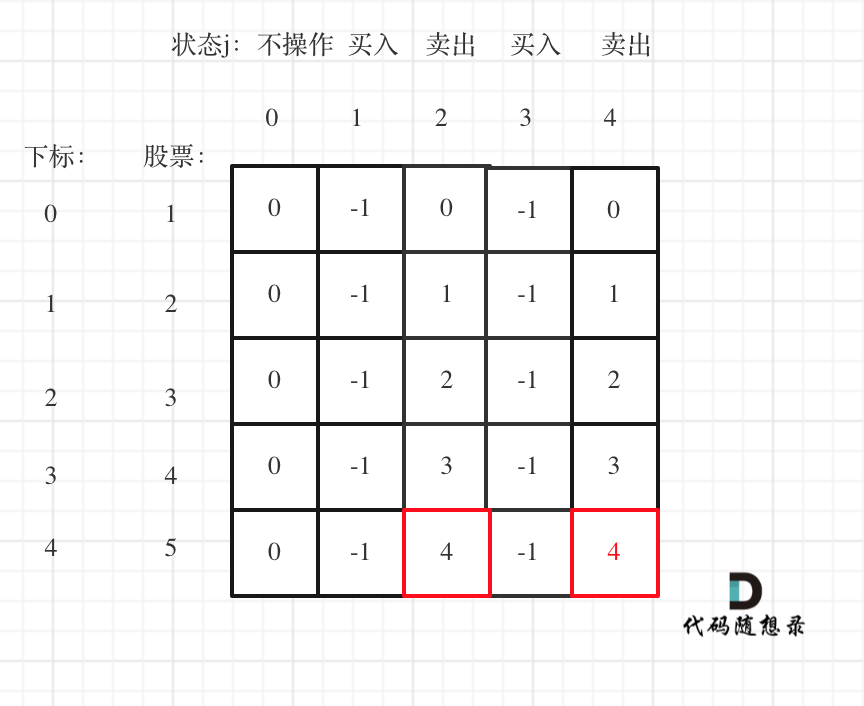
Notice the red box indicates the state of having sold stock twice.
In the end, the maximum must come from the sold states, particularly from the last state of having sold twice. If the first sale was the maximum, you could just buy and sell again on the same day. Thus, dp[4][4] encompasses the situation of dp[4][2]. Essentially, the final sell state holds the maximum profit.
So, the ultimate maximum profit is found at dp[4][4].
After detailing these five steps, we can easily derive the following code:
// Version 1
class Solution {
public:
int maxProfit(vector<int>& prices) {
if (prices.size() == 0) return 0;
vector<vector<int>> dp(prices.size(), vector<int>(5, 0));
dp[0][1] = -prices[0];
dp[0][3] = -prices[0];
for (int i = 1; i < prices.size(); i++) {
dp[i][0] = dp[i - 1][0];
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);
dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
}
return dp[prices.size() - 1][4];
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
- Time Complexity: O(n)
- Space Complexity: O(n × 5)
Additionally, there’s an optimized version regarding space, as seen in LeetCode’s official solution, which we provide in the C++ version below:
// Version 2
class Solution {
public:
int maxProfit(vector<int>& prices) {
if (prices.size() == 0) return 0;
vector<int> dp(5, 0);
dp[1] = -prices[0];
dp[3] = -prices[0];
for (int i = 1; i < prices.size(); i++) {
dp[1] = max(dp[1], dp[0] - prices[i]);
dp[2] = max(dp[2], dp[1] + prices[i]);
dp[3] = max(dp[3], dp[2] - prices[i]);
dp[4] = max(dp[4], dp[3] + prices[i]);
}
return dp[4];
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
- Time Complexity: O(n)
- Space Complexity: O(1)
Notice dp[2] utilizes dp[1] from the same day. Here’s a simple explanation:
If dp[1] extends the previous buy-in state, then dp[2] = max(dp[2], dp[1] + prices[i]); means selling today.
If dp[1] equals dp[0] - prices[i], today was a buy action, and dp[2] = max(dp[2], dp[1] + prices[i]); nullifies earnings, equivalent to no operation, retaining the cash position at yesterday’s sell state.
This simplified formulation may seem easier but tends to be convoluted. It's not advisable to follow this approach as it often leads to confusion!
Understanding and mastering the approach shown in Version 1 is sufficient for this problem!
# Further Discussion
Technically, the '0. No operation' state is unnecessary since, with no operation, cash remains at zero, similar to 0121.Best Time to Buy and Sell Stock (opens new window) and 0122.Best Time to Buy and Sell Stock II (opens new window).
Here is the following code:
// Version 3
class Solution {
public:
int maxProfit(vector<int>& prices) {
if (prices.size() == 0) return 0;
vector<vector<int>> dp(prices.size(), vector<int>(5, 0));
dp[0][1] = -prices[0];
dp[0][3] = -prices[0];
for (int i = 1; i < prices.size(); i++) {
dp[i][1] = max(dp[i - 1][1], 0 - prices[i]);
dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);
dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
}
return dp[prices.size() - 1][4];
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# Additional Language Versions
# Java:
// Version 1
class Solution {
public int maxProfit(int[] prices) {
int len = prices.length;
// Edge case check. As per the problem, length >= 1, can be omitted
if (prices.length == 0) return 0;
/*
* Define 5 states:
* 0: No operation, 1: First buy, 2: First sell, 3: Second buy, 4: Second sell
*/
int[][] dp = new int[len][5];
dp[0][1] = -prices[0];
// Initializing second buy ensures the result is maximum profit of up to two transactions
dp[0][3] = -prices[0];
for (int i = 1; i < len; i++) {
dp[i][1] = Math.max(dp[i - 1][1], -prices[i]);
dp[i][2] = Math.max(dp[i - 1][2], dp[i - 1][1] + prices[i]);
dp[i][3] = Math.max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
dp[i][4] = Math.max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
}
return dp[len - 1][4];
}
}
// Version 2: Space optimization
class Solution {
public int maxProfit(int[] prices) {
int[] dp = new int[4];
// Store states for two transactions
// dp[0] denotes first transaction buy
dp[0] = -prices[0];
// dp[1] denotes first transaction sell
dp[1] = 0;
// dp[2] denotes second transaction buy
dp[2] = -prices[0];
// dp[3] denotes second transaction sell
dp[3] = 0;
for(int i = 1; i <= prices.length; i++){
// Either no change, buy if none, sell if having
dp[0] = Math.max(dp[0], -prices[i-1]);
dp[1] = Math.max(dp[1], dp[0]+prices[i-1]);
// Second transaction, consider first transaction's sell profit
dp[2] = Math.max(dp[2], dp[1]-prices[i-1]);
dp[3] = Math.max(dp[3], dp[2]+ prices[i-1]);
}
return dp[3];
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
# Python:
Version 1:
class Solution:
def maxProfit(self, prices: List[int]) -> int:
if len(prices) == 0:
return 0
dp = [[0] * 5 for _ in range(len(prices))]
dp[0][1] = -prices[0]
dp[0][3] = -prices[0]
for i in range(1, len(prices)):
dp[i][0] = dp[i-1][0]
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i])
dp[i][2] = max(dp[i-1][2], dp[i-1][1] + prices[i])
dp[i][3] = max(dp[i-1][3], dp[i-1][2] - prices[i])
dp[i][4] = max(dp[i-1][4], dp[i-1][3] + prices[i])
return dp[-1][4]
2
3
4
5
6
7
8
9
10
11
12
13
14
Version 2:
class Solution:
def maxProfit(self, prices: List[int]) -> int:
if len(prices) == 0:
return 0
dp = [0] * 5
dp[1] = -prices[0]
dp[3] = -prices[0]
for i in range(1, len(prices)):
dp[1] = max(dp[1], dp[0] - prices[i])
dp[2] = max(dp[2], dp[1] + prices[i])
dp[3] = max(dp[3], dp[2] - prices[i])
dp[4] = max(dp[4], dp[3] + prices[i])
return dp[4]
2
3
4
5
6
7
8
9
10
11
12
13
# Go:
Version 1
func maxProfit(prices []int) int {
dp := make([][]int, len(prices))
for i := 0; i < len(prices); i++ {
dp[i] = make([]int, 5)
}
dp[0][0] = 0
dp[0][1] = -prices[0]
dp[0][2] = 0
dp[0][3] = -prices[0]
dp[0][4] = 0
for i := 1; i < len(prices); i++ {
dp[i][0] = dp[i-1][0]
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i])
dp[i][2] = max(dp[i-1][2], dp[i-1][1] + prices[i])
dp[i][3] = max(dp[i-1][3], dp[i-1][2] - prices[i])
dp[i][4] = max(dp[i-1][4], dp[i-1][3] + prices[i])
}
return dp[len(prices)-1][4]
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
Version 2
func maxProfit(prices []int) int {
if len(prices) == 0 {
return 0
}
dp := make([]int, 5)
dp[1] = -prices[0]
dp[3] = -prices[0]
for i := 1; i < len(prices); i++ {
dp[1] = max(dp[1], dp[0] - prices[i])
dp[2] = max(dp[2], dp[1] + prices[i])
dp[3] = max(dp[3], dp[2] - prices[i])
dp[4] = max(dp[4], dp[3] + prices[i])
}
return dp[4]
}
func max(x, y int) int {
if x > y {
return x
}
return y
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Version 3
func maxProfit(prices []int) int {
if len(prices) == 0 {
return 0
}
dp := make([][5]int, len(prices))
dp[0][1] = -prices[0]
dp[0][3] = -prices[0]
for i := 1; i < len(prices); i++ {
dp[i][1] = max(dp[i-1][1], 0 - prices[i])
dp[i][2] = max(dp[i-1][2], dp[i-1][1] + prices[i])
dp[i][3] = max(dp[i-1][3], dp[i-1][2] - prices[i])
dp[i][4] = max(dp[i-1][4], dp[i-1][3] + prices[i])
}
return dp[len(prices)-1][4]
}
func max(x, y int) int {
if x > y {
return x
}
return y
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Version 4: In a one-dimensional easy-to-understand dp
func maxProfit(prices []int) int {
dp := make([]int, 4)
dp[0] = -prices[0]
dp[2] = -prices[0]
for _, price := range prices[1:] {
dc := slices.Clone(dp) // The key part, preserve the previous day's dp state to prevent overwriting, thus only utilize this, not dp, resulting in a simple, comprehensible logic
dp[0] = max(dc[0], -price)
dp[1] = max(dc[1], dc[0] + price)
dp[2] = max(dc[2], dc[1] - price)
dp[3] = max(dc[3], dc[2] + price)
}
return dp[3]
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# JavaScript:
Version 1:
const maxProfit = prices => {
const len = prices.length;
const dp = new Array(len).fill(0).map(x => new Array(5).fill(0));
dp[0][1] = -prices[0];
dp[0][3] = -prices[0];
for (let i = 1; i < len; i++) {
dp[i][0] = dp[i - 1][0];
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
dp[i][2] = Math.max(dp[i - 1][2], dp[i - 1][1] + prices[i]);
dp[i][3] = Math.max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
dp[i][4] = Math.max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
}
return dp[len - 1][4];
};
2
3
4
5
6
7
8
9
10
11
12
13
14
Version 2:
const maxProfit = prices => {
const len = prices.length;
const dp = new Array(5).fill(0);
dp[1] = -prices[0];
dp[3] = -prices[0];
for (let i = 1; i < len; i++) {
dp[1] = Math.max(dp[1], dp[0] - prices[i]);
dp[2] = Math.max(dp[2], dp[1] + prices[i]);
dp[3] = Math.max(dp[3], dp[2] - prices[i]);
dp[4] = Math.max(dp[4], dp[3] + prices[i]);
}
return dp[4];
};
2
3
4
5
6
7
8
9
10
11
12
13
# TypeScript:
Version 1
function maxProfit(prices: number[]): number {
/**
dp[i][0]: No operation;
dp[i][1]: First buy;
dp[i][2]: First sell;
dp[i][3]: Second buy;
dp[i][4]: Second sell;
*/
const length: number = prices.length;
if (length === 0) return 0;
const dp: number[][] = new Array(length).fill(0)
.map(_ => new Array(5).fill(0));
dp[0][1] = -prices[0];
dp[0][3] = -prices[0];
for (let i = 1; i < length; i++) {
dp[i][0] = dp[i - 1][0];
dp[i][1] = Math.max(dp[i - 1][1], -prices[i]);
dp[i][2] = Math.max(dp[i - 1][2], dp[i - 1][1] + prices[i]);
dp[i][3] = Math.max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
dp[i][4] = Math.max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
}
return Math.max(dp[length - 1][2], dp[length - 1][4]);
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# C:
#define max(a, b) ((a) > (b) ? (a) : (b))
#define min(a, b) ((a) > (b) ? (b) : (a))
int maxProfit(int* prices, int pricesSize) {
int buy1 = prices[0], buy2 = prices[0];
int profit1 = 0, profit2 = 0;
for (int i = 0; i < pricesSize; ++i) {
// Find the minimum purchase point
buy1 = min(buy1, prices[i]);
// Calculate maximum profit for the first transaction, keep updating this
profit1 = max(profit1, prices[i] - buy1);
// Calculate the cost for buying the second stock, considering the profit from the first sell
// Current price - profit from first transaction = new investment cost
// To maximize profit, find the minimum cost
buy2 = min(buy2, prices[i] - profit1);
// Profit after the second sell: current price minus cost, keep updating this maximum profit
profit2 = max(profit2, prices[i] - buy2);
}
return profit2;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# Rust:
Version 1
impl Solution {
pub fn max_profit(prices: Vec<i32>) -> i32 {
/*
* Define 5 states:
* 0: No operation, 1: First buy, 2: First sell, 3: Second buy, 4: Second sell
*/
let mut dp = vec![vec![0; 5]; prices.len()];
dp[0][1] = -prices[0];
dp[0][3] = -prices[0];
for (i, &p) in prices.iter().enumerate().skip(1) {
// No operation
// dp[i][0] = dp[i - 1][0];
dp[i][1] = dp[i - 1][1].max(-p);
dp[i][2] = dp[i - 1][2].max(dp[i - 1][1] + p);
dp[i][3] = dp[i - 1][3].max(dp[i - 1][2] - p);
dp[i][4] = dp[i - 1][4].max(dp[i - 1][3] + p);
}
dp[prices.len() - 1][4]
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Version 2
impl Solution {
pub fn max_profit(prices: Vec<i32>) -> i32 {
let (mut one_buy, mut one_sale, mut two_buy, mut two_sale) = (-prices[0], 0, -prices[0], 0);
for p in prices {
one_buy = one_buy.max(-p);
one_sale = one_sale.max(p + one_buy);
two_buy = two_buy.max(one_sale - p);
two_sale = two_sale.max(two_buy + p);
}
two_sale
}
}
2
3
4
5
6
7
8
9
10
11
12
13
