516. Longest Palindromic Subsequence

LeetCode problem link (opens new window)

Given a string s, find the longest palindromic subsequence in it and return its length. You may assume that the maximum length of s is 1000.

Example 1: Input: "bbbab" Output: 4 A possible longest palindromic subsequence is "bbbb".

Example 2: Input: "cbbd" Output: 2 A possible longest palindromic subsequence is "bb".

Constraints:

• 1 <= s.length <= 1000
• s consists only of lowercase English letters

Thought Process

We recently discussed dynamic programming on palindromic substrings (opens new window), which focuses on palindromic substrings, but this problem requires finding a palindromic subsequence. It's important to understand the distinction between the two.

Palindromic substrings are contiguous, while palindromic subsequences are not contiguous! Both are classic problems in dynamic programming.

For palindromic substrings, you can also try these:

• 647. Palindromic Substrings
• 5. Longest Palindromic Substring

The thought process is somewhat similar, but this problem is slightly simpler as it involves fewer cases.

Let's analyze the five steps of dynamic programming for this problem:

1. Define the dp array (dp table) and the meaning of its indices

dp[i][j]: the length of the longest palindromic subsequence in the substring s[i:j].

2. Determine the recurrence formula

In the problem of palindromic substrings, a crucial part is checking whether s[i] equals s[j].

If s[i] equals s[j], then dp[i][j] = dp[i + 1][j - 1] + 2;

As illustrated:

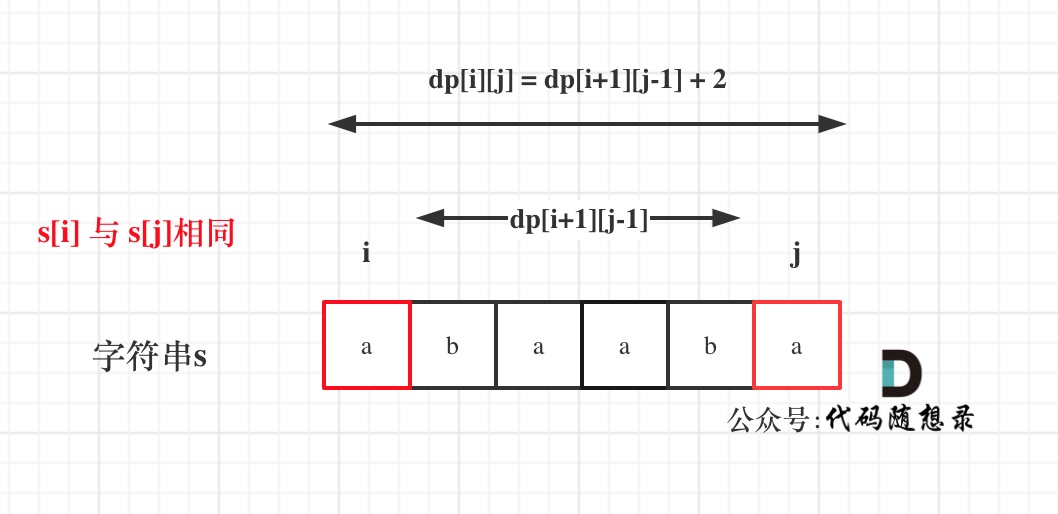
(If you don't understand this, recall the definition of dp[i][j])

If s[i] does not equal s[j], it indicates that simultaneously adding s[i] and s[j] does not increase the length of the palindromic subsequence in the range [i,j]. Therefore, consider adding either s[j] or s[i] separately to see which can form the longest palindromic subsequence.

Adding s[j] results in the palindromic subsequence of length dp[i + 1][j].

Adding s[i] results in the palindromic subsequence of length dp[i][j - 1].

Hence, dp[i][j] would be the maximum among them, i.e., dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);

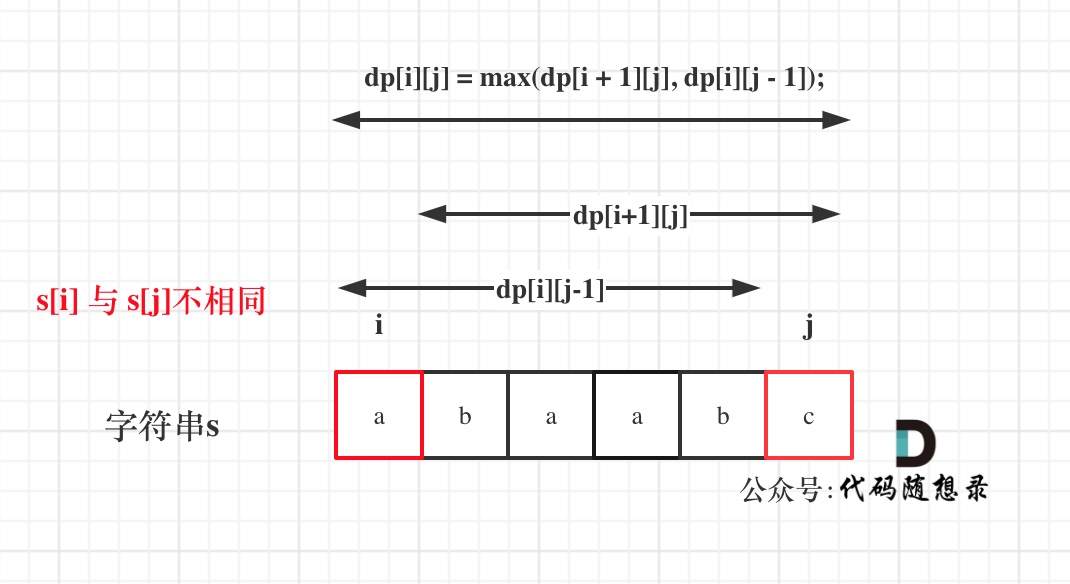
The code is as follows:

if (s[i] == s[j]) {
    dp[i][j] = dp[i + 1][j - 1] + 2;
} else {
    dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
}

3. Initialize the dp array

First, consider the situation when i equals j. From the recurrence formula: dp[i][j] = dp[i + 1][j - 1] + 2;, you can see that this formula cannot calculate cases where i and j are the same.

Thus, you have to manually initialize: when i equals j, then dp[i][j] must be 1, which means the length of a palindromic subsequence of a single character is 1.

For other cases, you can initialize dp[i][j] to 0 so that in the recurrence formula: dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);, dp[i][j] will not be overwritten by the initial value.

vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0));
for (int i = 0; i < s.size(); i++) dp[i][i] = 1;

4. Determine the order of traversal

From the recurrence formula, it is clear that dp[i][j] depends on dp[i + 1][j - 1], dp[i + 1][j], and dp[i][j - 1], as shown:

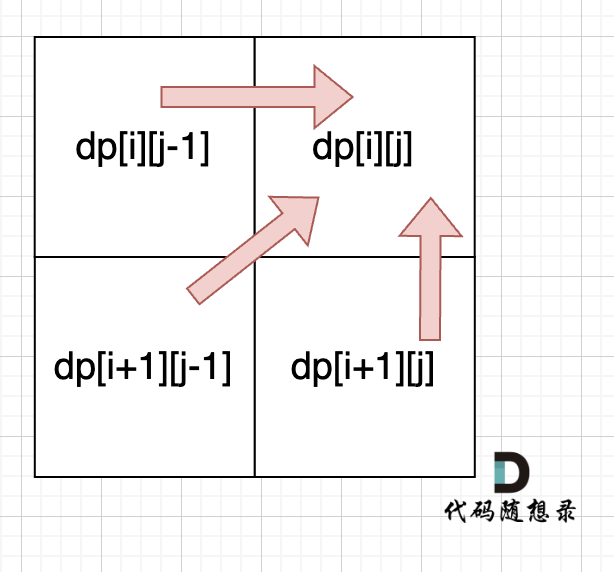
Thus, when iterating over i, you need to iterate from bottom to top to ensure that the next row's data is computed.

For j, it can be traversed normally from left to right.

The code is as follows:

for (int i = s.size() - 1; i >= 0; i--) {
    for (int j = i + 1; j < s.size(); j++) {
        if (s[i] == s[j]) {
            dp[i][j] = dp[i + 1][j - 1] + 2;
        } else {
            dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
        }
    }
}

5. Example trace of the dp array

For an input s:"cbbd", the dp array states are as shown:

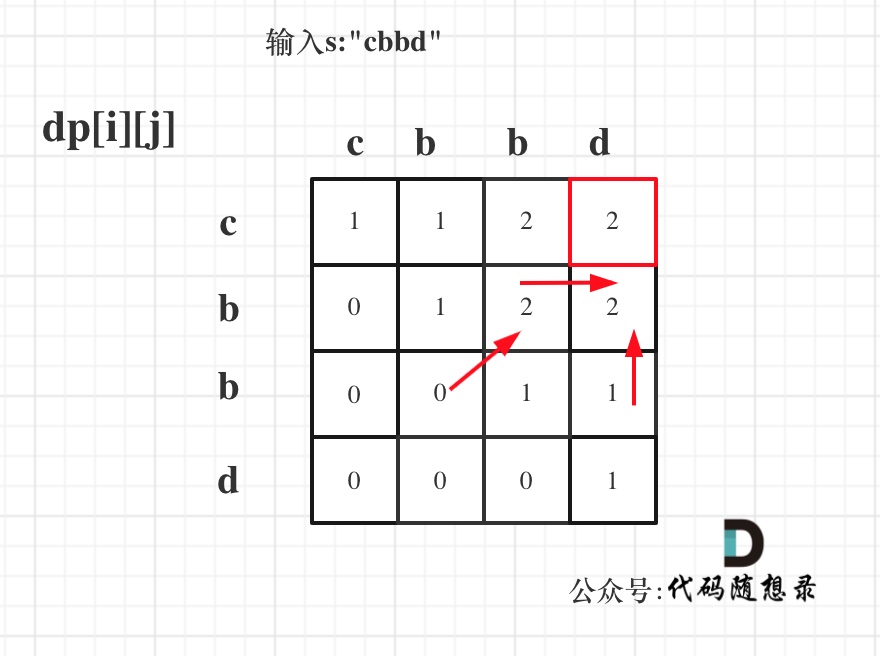
The red box displays the final result: dp[0][s.size() - 1];

With the above analysis, the C++ code is as follows:

class Solution {
public:
    int longestPalindromeSubseq(string s) {
        vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0));
        for (int i = 0; i < s.size(); i++) dp[i][i] = 1;
        for (int i = s.size() - 1; i >= 0; i--) {
            for (int j = i + 1; j < s.size(); j++) {
                if (s[i] == s[j]) {
                    dp[i][j] = dp[i + 1][j - 1] + 2;
                } else {
                    dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[0][s.size() - 1];
    }
};

• Time complexity: O(n^2)
• Space complexity: O(n^2)

Versions in other languages

Java:

public class Solution {
    public int longestPalindromeSubseq(String s) {
        int len = s.length();
        int[][] dp = new int[len + 1][len + 1];
        for (int i = len - 1; i >= 0; i--) { // iterate from the end to ensure no missed cases
            dp[i][i] = 1; // initialization
            for (int j = i + 1; j < len; j++) {
                if (s.charAt(i) == s.charAt(j)) {
                    dp[i][j] = dp[i + 1][j - 1] + 2;
                } else {
                    dp[i][j] = Math.max(dp[i + 1][j], Math.max(dp[i][j], dp[i][j - 1]));
                }
            }
        }
        return dp[0][len - 1];
    }
}

Python:

class Solution:
    def longestPalindromeSubseq(self, s: str) -> int:
        dp = [[0] * len(s) for _ in range(len(s))]
        for i in range(len(s)):
            dp[i][i] = 1
        for i in range(len(s)-1, -1, -1):
            for j in range(i+1, len(s)):
                if s[i] == s[j]:
                    dp[i][j] = dp[i+1][j-1] + 2
                else:
                    dp[i][j] = max(dp[i+1][j], dp[i][j-1])
        return dp[0][-1]

Go:

func longestPalindromeSubseq(s string) int {
	size := len(s)
	max := func(a, b int) int {
		if a > b {
			return a
		}
		return b
	}
	dp := make([][]int, size)
	for i := 0; i < size; i++ {
		dp[i] = make([]int, size)
		dp[i][i] = 1
	}
	for i := size - 1; i >= 0; i-- {
		for j := i + 1; j < size; j++ {
			if s[i] == s[j] {
				dp[i][j] = dp[i+1][j-1] + 2
			} else {
				dp[i][j] = max(dp[i][j-1], dp[i+1][j])
			}
		}
	}
	return dp[0][size-1]
}

JavaScript:

const longestPalindromeSubseq = (s) => {
    const strLen = s.length;
    let dp = Array.from(Array(strLen), () => Array(strLen).fill(0));

    for(let i = 0; i < strLen; i++) {
        dp[i][i] = 1;
    }

    for(let i = strLen - 1; i >= 0; i--) {
        for(let j = i + 1; j < strLen; j++) {
            if(s[i] === s[j]) {
                dp[i][j] = dp[i+1][j-1] + 2;
            } else {
                dp[i][j] = Math.max(dp[i+1][j], dp[i][j-1]);
            }
        }
    }

    return dp[0][strLen - 1];
};

TypeScript:

function longestPalindromeSubseq(s: string): number {
    /**
        dp[i][j]: length of longest palindromic subsequence in range [i,j]
     */
    const length: number = s.length;
    const dp: number[][] = new Array(length).fill(0)
        .map(_ => new Array(length).fill(0));
    for (let i = 0; i < length; i++) {
        dp[i][i] = 1;
    }
    // Bottom-up and left-to-right iteration
    for (let i = length - 1; i >= 0; i--) {
        for (let j = i + 1; j < length; j++) {
            if (s[i] === s[j]) {
                dp[i][j] = dp[i + 1][j - 1] + 2;
            } else {
                dp[i][j] = Math.max(dp[i][j - 1], dp[i + 1][j]);
            }
        }
    }
    return dp[0][length - 1];
};

Rust:

impl Solution {
    pub fn longest_palindrome_subseq(s: String) -> i32 {
        let mut dp = vec![vec![0; s.len()]; s.len()];
        for i in (0..s.len()).rev() {
            dp[i][i] = 1;
            for j in i + 1..s.len() {
                if s[i..=i] == s[j..=j] {
                    dp[i][j] = dp[i + 1][j - 1] + 2;
                    continue;
                }
                dp[i][j] = dp[i + 1][j].max(dp[i][j - 1]);
            }
        }
        dp[0][s.len() - 1]
    }
}