keetcoder

# 474. Ones and Zeroes

LeetCode Problem Link (opens new window)

Given a binary string array strs and two integers m and n.

Find the size of the largest subset of strs that contains at most m zeros and n ones.

A subset x is a subset of y if all elements of x are also elements of y.

Example 1:

  • Input: strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3

  • Output: 4

  • Explanation: The largest subset that contains at most 5 zeros and 3 ones is {"10","0001","1","0"}, so the answer is 4. Other subsets that meet the conditions but are smaller include {"0001","1"} and {"10","1","0"}. {"111001"} does not meet the condition because it contains 4 ones, which is more than the allowed 3.

Example 2:

  • Input: strs = ["10", "0", "1"], m = 1, n = 1
  • Output: 2
  • Explanation: The largest subset is {"0", "1"}, so the answer is 2.

Constraints:

  • 1 <= strs.length <= 600
  • 1 <= strs[i].length <= 100
  • strs[i] consists only of '0' and '1'.
  • 1 <= m, n <= 100

# Thought Process

If you're not familiar with the knapsack problem, first check out these two articles:

This problem can be a bit tricky, somewhat like a brain teaser programmers pose to themselves. Why make it harder for programmers?

About this problem, some may think of it as a multi-knapsack problem, and some explanations are written this way.

However, this problem is not a multi-knapsack problem. Let's review with this diagram to clarify the different types of knapsack problems:

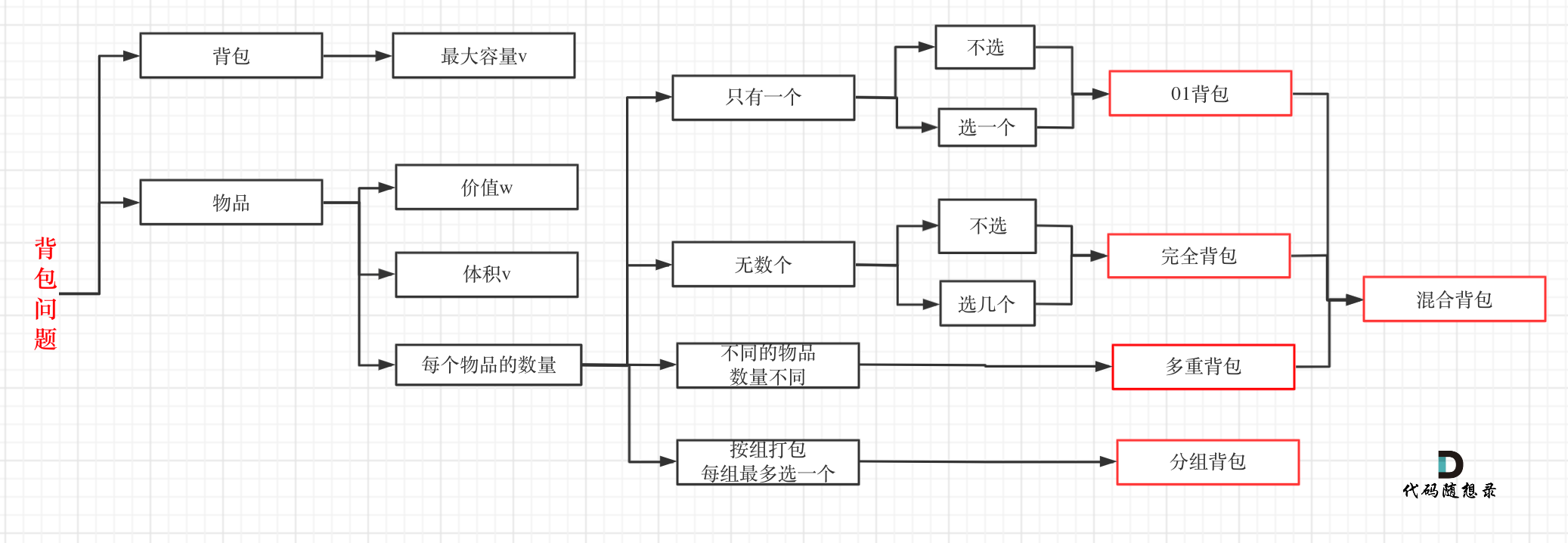
416.分割等和子集1

The multiple knapsack problem deals with items that have different quantities.

In this problem, the elements in the strs array are the items, and each item represents one!

The values m and n are analogous to a knapsack, but with two dimensions.

Some might confuse m and n as different items, feeling it's a multiple knapsack problem.

But this problem is actually a 0-1 knapsack problem!

Although, this knapsack has two dimensions, one being m and the other being n. Different lengths of strings are items of varying sizes waiting to be packed.

Let's start the five-step dynamic programming process:

  1. Define the dp array (dp table) and the meaning of the indices

dp[i][j]: The maximum size of the subset of strs with at most i zeros and j ones is dp[i][j].

  1. Establish the recurrence relation

dp[i][j] can be derived from the previous string in strs, each string containing zeroNum zeros, and oneNum ones.

dp[i][j] can be dp[i - zeroNum][j - oneNum] + 1.

During iteration, we take the maximum value of dp[i][j].

So the recurrence relation is: dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);

At this point, recall the recurrence relation of the 0-1 knapsack: dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

You'll find that the zeroNum and oneNum of strings are like the weights of items (weight[i]), while the count of items itself is like the item's value (value[i]).

This is a classic 0-1 knapsack problem! Just with item weights having two dimensions.

  1. Initialize the dp array

In Dynamic Programming: Knapsack Theory 01 Knapsack-2 (opens new window), we explained how initializing the 0-1 knapsack dp array to 0 suffices.

Since item values won't be negative, initializing with 0 ensures the dp[i][j] won't be overwritten.

  1. Determine the iteration order

In Dynamic Programming: Knapsack Theory 01 Knapsack-2 (opens new window), it's explained why the 0-1 knapsack iterates in this order: outer for loop iterating over items, inner for loop iterating over knapsack capacities, and iterating from back to front.

Thus, for this problem, items are strings in strs, and the knapsack capacities are the m and n described in the problem statement.

Here's the code:

for (string str : strs) { // iterate over items
    int oneNum = 0, zeroNum = 0;
    for (char c : str) {
        if (c == '0') zeroNum++;
        else oneNum++;
    }
    for (int i = m; i >= zeroNum; i--) { // iterate over the knapsack's capacity from back to front!
        for (int j = n; j >= oneNum; j--) {
            dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12

Some may wonder if the order of these two for loops matters?

It doesn't; they're both a dimension of item weights, so starting with either is fine!

  1. Example walkthrough for the dp array

Using the input ["10", "0001", "111001", "1", "0"], m = 3, n = 3 as an example:

The resulting dp array looks as follows:

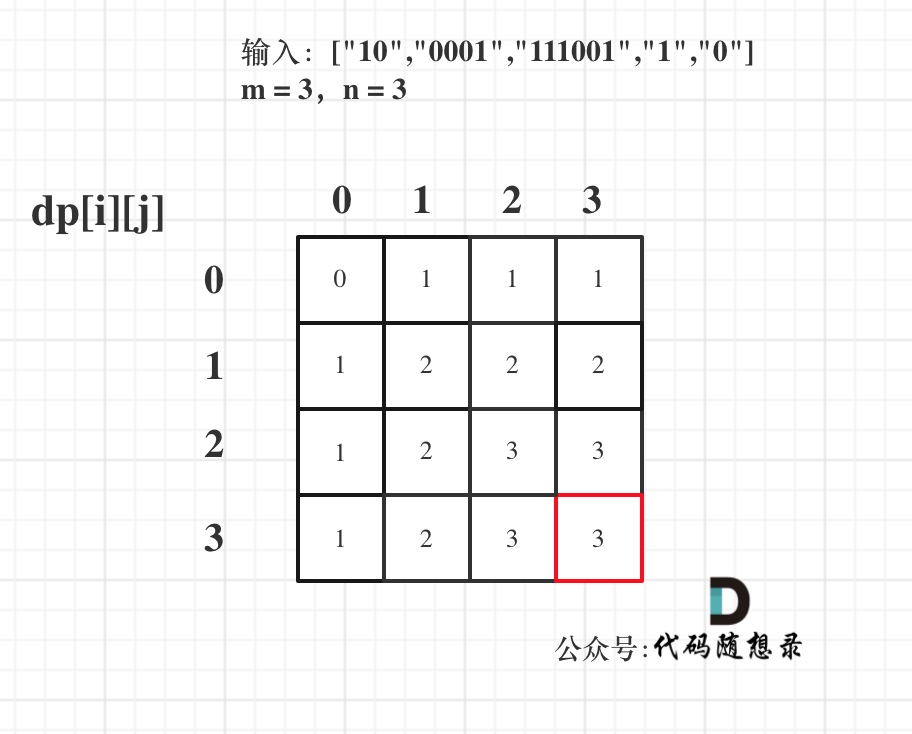
474. Ones and Zeroes

The dynamic programming five-step analysis is now complete, and the C++ code is as follows:

class Solution {
public:
    int findMaxForm(vector<string>& strs, int m, int n) {
        vector<vector<int>> dp(m + 1, vector<int> (n + 1, 0)); // initialize to 0
        for (string str : strs) { // iterate over items
            int oneNum = 0, zeroNum = 0;
            for (char c : str) {
                if (c == '0') zeroNum++;
                else oneNum++;
            }
            for (int i = m; i >= zeroNum; i--) { // iterate over the knapsack capacity from back to front!
                for (int j = n; j >= oneNum; j--) {
                    dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
                }
            }
        }
        return dp[m][n];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
  • Time complexity: O(kmn), where k is the length of strs
  • Space complexity: O(mn)

C++: Version using three-dimensional array

class Solution {
public:
    int findMaxForm(vector<string>& strs, int m, int n) {
        int num_of_str = strs.size();

		vector<vector<vector<int>>> dp(num_of_str, vector<vector<int>>(m + 1,vector<int>(n + 1, 0)));

		/* 	dp[i][j][k] represents, if choosing items among strs[0] to strs[i] to form a subset, 
			what is the maximum size of this subset such that there are no more than m 0's and n 1's in this subset. 
			Each entry of dp[i][j][k] is initialized with 0
			
			transition formula:
			using x[i] to indicates the number of 0's in strs[i]
			using y[i] to indicates the number of 1's in strs[i]
			
			dp[i][j][k] = max(dp[i-1][j][k], dp[i-1][j - x[i]][k - y[i]] + 1)

		*/


		// num_of_zeros records the number of 0's for each str
		// num_of_ones records the number of 1's for each str
		// find the number of 0's and the number of 1's for each str in strs
		vector<int> num_of_zeros;
		vector<int> num_of_ones;
		for (auto& str : strs){
			int count_of_zero = 0;
			int count_of_one = 0;
			for (char &c : str){
				if(c == '0') count_of_zero ++;
				else count_of_one ++;
			}
			num_of_zeros.push_back(count_of_zero);
			num_of_ones.push_back(count_of_one);
			
		}

		
		// num_of_zeros[0] indicates the number of 0's for str[0]
		// num_of_ones[0] indiates the number of 1's for str[1]

		// initialize the 1st plane of dp[i][j][k], i.e., dp[0][j][k]
		// if num_of_zeros[0] > m or num_of_ones[0] > n, no need to further initialize dp[0][j][k], 
		// because they have been intialized to 0 previously
		if(num_of_zeros[0] <= m && num_of_ones[0] <= n){
			// for j < num_of_zeros[0] or k < num_of_ones[0], dp[0][j][k] = 0
			for(int j = num_of_zeros[0]; j <= m; j++){
				for(int k = num_of_ones[0]; k <= n; k++){
					dp[0][j][k] = 1;
				}
			}
		}

		/*	if j - num_of_zeros[i] >= 0 and k - num_of_ones[i] >= 0:
				dp[i][j][k] = max(dp[i-1][j][k], dp[i-1][j - num_of_zeros[i]][k - num_of_ones[i]] + 1)  
			else:
				dp[i][j][k] = dp[i-1][j][k]
		*/

		for (int i = 1; i < num_of_str; i++){
			int count_of_zeros = num_of_zeros[i];
			int count_of_ones = num_of_ones[i]; 
			for (int j = 0; j <= m; j++){
				for (int k = 0; k <= n; k++){
					if( j < count_of_zeros || k < count_of_ones){
						dp[i][j][k] = dp[i-1][j][k];
					}else{
						dp[i][j][k] = max(dp[i-1][j][k], dp[i-1][j - count_of_zeros][k - count_of_ones] + 1);
					}
				}
			}
			
		}

		return dp[num_of_str-1][m][n];

    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78

# Summary

Some might have encountered this problem and not realized what kind of knapsack it actually is.

This time, we've unlocked several applications of the 0-1 knapsack:

The examples in "Code Thinking Notes" showcase 0-1 knapsack applications across different dimensions, offering a chance to savor each one deeply!

# Versions in Other Programming Languages

# Java

Three-dimensional DP array implementation

class Solution {
    public int findMaxForm(String[] strs, int m, int n) {
        /// The array has three dimensions
        // The first dimension: choose from the first few strings
        // The second dimension: limit of zeros (knapsack dimension 1)
        // The third dimension: limit of ones (knapsack dimension 2)
        int[][][] dpArr = new int[strs.length][m + 1][n + 1];

        /// Initialize the dpArr array
        // Calculate the number of zeros and ones in the first string
        int zeroNum = 0;
        int oneNum = 0;
        for (char c : strs[0].toCharArray()) {
            if (c == '0') {
                zeroNum++;
            } else {
                oneNum++;
            }
        }
        // When the number of zeros and ones fits the first string, initialize the corresponding positions of the DP array to 1, as the current subset count is 1
        for (int j = zeroNum; j <= m; j++) {
            for (int k = oneNum; k <= n; k++) {
                dpArr[0][j][k] = 1;
            }
        }
        /// Fill in the DP array after adding the i-th string
        for (int i = 1; i < strs.length; i++) {
            zeroNum = 0;
            oneNum = 0;
            for (char c : strs[i].toCharArray()) {
                if (c == '0') {
                    zeroNum++;
                } else {
                    oneNum++;
                }
            }
            for (int j = 0; j <= m; j++) {
                for (int k = 0; k <= n; k++) {
                    if (j >= zeroNum && k >= oneNum) {
                        // --if-- When both the zero dimension and the one dimension capacity are greater than or equal to the current string's zero and one count, consider whether to put the current string in the knapsack
                        // Not putting in the i-th string, the subset count remains dpArr[i - 1][j][k]
                        // Putting in the i-th string requires vacating zeroNum spaces in dimension 1 and oneNum spaces in dimension 2, then putting in the current string, i.e., dpArr[i - 1][j - zeroNum][k - oneNum] + 1)
                        dpArr[i][j][k] = Math.max(dpArr[i - 1][j][k], dpArr[i - 1][j - zeroNum][k - oneNum] + 1);
                    } else {
                        // --if-- Unable to put in the i-th string, the subset count remains dpArr[i - 1][j][k]
                        dpArr[i][j][k] = dpArr[i - 1][j][k];
                    }
                }
            }
        }
        return dpArr[dpArr.length - 1][m][n];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

Two-dimensional DP array implementation

class Solution {
    public int findMaxForm(String[] strs, int m, int n) {
        //dp[i][j] indicates the largest subset with i zeros and j ones
        int[][] dp = new int[m + 1][n + 1];
        int oneNum, zeroNum;
        for (String str : strs) {
            oneNum = 0;
            zeroNum = 0;
            for (char ch : str.toCharArray()) {
                if (ch == '0') {
                    zeroNum++;
                } else {
                    oneNum++;
                }
            }
            // Iterate in reverse order
            for (int i = m; i >= zeroNum; i--) {
                for (int j = n; j >= oneNum; j--) {
                    dp[i][j] = Math.max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
                }
            }
        }
        return dp[m][n];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

# Python

DP (Version 1)

class Solution:
    def findMaxForm(self, strs: List[str], m: int, n: int) -> int:
        dp = [[0] * (n + 1) for _ in range(m + 1)]  # Initialize 2D dynamic programming array to 0
        for s in strs:  # Iterate over items
            zeroNum = s.count('0')  # Count zeros
            oneNum = len(s) - zeroNum  # Count ones
            for i in range(m, zeroNum - 1, -1):  # Iterate over knapsack capacity from back to front
                for j in range(n, oneNum - 1, -1):
                    dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1)  # Recurrence relation
        return dp[m][n]
1
2
3
4
5
6
7
8
9
10
11

DP (Version 2)

class Solution:
    def findMaxForm(self, strs: List[str], m: int, n: int) -> int:
        dp = [[0] * (n + 1) for _ in range(m + 1)]  # Initialize 2D dynamic programming array to 0
        # Iterate over items
        for s in strs:
            ones = s.count('1')  # Count ones in string
            zeros = s.count('0')  # Count zeros in string
            # Iterate over knapsack capacity from back to front
            for i in range(m, zeros - 1, -1):
                for j in range(n, ones - 1, -1):
                    dp[i][j] = max(dp[i][j], dp[i - zeros][j - ones] + 1)  # Recurrence relation
        return dp[m][n]
1
2
3
4
5
6
7
8
9
10
11
12
13

# Go

func findMaxForm(strs []string, m int, n int) int {
	// Define array
	dp := make([][]int, m+1)
	for i,_ := range dp {
		dp[i] = make([]int, n+1 )
	}
	// Iterate
	for i:=0;i<len(strs);i++ {
		zeroNum,oneNum := 0 , 0
		// Count 0s and 1s
		// Or directly use strings.Count(strs[i],"0")
		for _,v := range strs[i] {
			if v == '0' {
				zeroNum++
			}
		}
		oneNum = len(strs[i])-zeroNum
		// Iterate knapsack capacity in reverse
		for j:= m ; j >= zeroNum;j-- {
			for k:=n ; k >= oneNum;k-- {
				// Recurrence formula
				dp[j][k] = max(dp[j][k],dp[j-zeroNum][k-oneNum]+1)
			}
		}
		//fmt.Println(dp)
	}
	return dp[m][n]
}

func max(a,b int) int {
	if a > b {
		return a
	}
	return b
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

# JavaScript

const findMaxForm = (strs, m, n) => {
    const dp = Array.from(Array(m+1), () => Array(n+1).fill(0));
    let numOfZeros, numOfOnes;

    for(let str of strs) {
        numOfZeros = 0;
        numOfOnes = 0;
    
        for(let c of str) {
            if (c === '0') {
                numOfZeros++;
            } else {
                numOfOnes++;
            }
        }

        for(let i = m; i >= numOfZeros; i--) {
            for(let j = n; j >= numOfOnes; j--) {
                dp[i][j] = Math.max(dp[i][j], dp[i - numOfZeros][j - numOfOnes] + 1);
            }
        }
    }

    return dp[m][n];
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

# TypeScript

Rolling array, two-dimensional array method

type BinaryInfo = { numOfZero: number, numOfOne: number };
function findMaxForm(strs: string[], m: number, n: number): number {
    const goodsNum: number = strs.length;
    const dp: number[][] = new Array(m + 1).fill(0)
        .map(_ => new Array(n + 1).fill(0));
    for (let i = 0; i < goodsNum; i++) {
        const { numOfZero, numOfOne } = countBinary(strs[i]);
        for (let j = m; j >= numOfZero; j--) {
            for (let k = n; k >= numOfOne; k--) {
                dp[j][k] = Math.max(dp[j][k], dp[j - numOfZero][k - numOfOne] + 1);
            }
        }
    }
    return dp[m][n];
};
function countBinary(str: string): BinaryInfo {
    let numOfZero: number = 0,
        numOfOne: number = 0;
    for (let s of str) {
        if (s === '0') {
            numOfZero++;
        } else {
            numOfOne++;
        }
    }
    return { numOfZero, numOfOne };
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

Traditional knapsack, three-dimensional array method

type BinaryInfo = { numOfZero: number, numOfOne: number };
function findMaxForm(strs: string[], m: number, n: number): number {
    /**
        dp[i][j][k]: front i-th item, 0 capacity of knapsack is j, 1 capacity is k, most items count
     */
    const goodsNum: number = strs.length;
    const dp: number[][][] = new Array(goodsNum).fill(0)
        .map(_ => new Array(m + 1)
            .fill(0)
            .map(_ => new Array(n + 1).fill(0))
        );
    const { numOfZero, numOfOne } = countBinary(strs[0]);
    for (let i = numOfZero; i <= m; i++) {
        for (let j = numOfOne; j <= n; j++) {
            dp[0][i][j] = 1;
        }
    }
    for (let i = 1; i < goodsNum; i++) {
        const { numOfZero, numOfOne } = countBinary(strs[i]);
        for (let j = 0; j <= m; j++) {
            for (let k = 0; k <= n; k++) {
                if (j < numOfZero || k < numOfOne) {
                    dp[i][j][k] = dp[i - 1][j][k];
                } else {
                    dp[i][j][k] = Math.max(dp[i - 1][j][k], dp[i - 1][j - numOfZero][k - numOfOne] + 1);
                }
            }
        }
    }
    return dp[dp.length - 1][m][n];
};
function countBinary(str: string): BinaryInfo {
    let numOfZero: number = 0,
        numOfOne: number = 0;
    for (let s of str) {
        if (s === '0') {
            numOfZero++;
        } else {
            numOfOne++;
        }
    }
    return { numOfZero, numOfOne };
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

Backtracking method (will timeout)

function findMaxForm(strs: string[], m: number, n: number): number {
    /**
        Thought: Brutally enumerate all subsets of strs, record the maximum length of the subsets that meet the conditions
     */
    let resMax: number = 0;
    backTrack(strs, m, n, 0, []);
    return resMax;
    function backTrack(
        strs: string[], m: number, n: number,
        startIndex: number, route: string[]
    ): void {
        if (startIndex === strs.length) return;
        for (let i = startIndex, length = strs.length; i < length; i++) {
            route.push(strs[i]);
            if (isValidSubSet(route, m, n)) {
                resMax = Math.max(resMax, route.length);
                backTrack(strs, m, n, i + 1, route);
            }
            route.pop();
        }
    }
};
function isValidSubSet(strs: string[], m: number, n: number): boolean {
    let zeroNum: number = 0,
        oneNum: number = 0;
    strs.forEach(str => {
        for (let s of str) {
            if (s === '0') {
                zeroNum++;
            } else {
                oneNum++;
            }
        }
    });
    return zeroNum <= m && oneNum <= n;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

# Scala

Knapsack:

object Solution {
  def findMaxForm(strs: Array[String], m: Int, n: Int): Int = {
    var dp = Array.ofDim[Int](m + 1, n + 1)

    var (oneNum, zeroNum) = (0, 0)

    for (str <- strs) {
      oneNum = 0
      zeroNum = 0
      for (i <- str.indices) {
        if (str(i) == '0') zeroNum += 1
        else oneNum += 1
      }

      for (i <- m to zeroNum by -1) {
        for (j <- n to oneNum by -1) {
          dp(i)(j) = math.max(dp(i)(j), dp(i - zeroNum)(j - oneNum) + 1)
        }
      }
    }

    dp(m)(n)
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

Backtracking method (timed out):

object Solution {
  import scala.collection.mutable

  var res = Int.MinValue

  def test(str: String): (Int, Int) = {
    var (zero, one) = (0, 0)
    for (i <- str.indices) {
      if (str(i) == '1') one += 1
      else zero += 1
    }
    (zero, one)
  }

  def travsel(strs: Array[String], path: mutable.ArrayBuffer[String], m: Int, n: Int, startIndex: Int): Unit = {
    if (startIndex > strs.length) {
      return
    }

    res = math.max(res, path.length)

    for (i <- startIndex until strs.length) {

      var (zero, one) = test(strs(i))

      // If the number of zeros is less than m and the number of ones is less than n, then backtrack
      if (zero <= m && one <= n) {
        path.append(strs(i))
        travsel(strs, path, m - zero, n - one, i + 1)
        path.remove(path.length - 1)
      }
    }
  }

  def findMaxForm(strs: Array[String], m: Int, n: Int): Int = {
    res = Int.MinValue
    var path = mutable.ArrayBuffer[String]()
    travsel(strs, path, m, n, 0)
    res
  }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

# Rust

impl Solution {
    pub fn find_max_form(strs: Vec<String>, m: i32, n: i32) -> i32 {
        let (m, n) = (m as usize, n as usize);
        let mut dp = vec![vec![0; n + 1]; m + 1];
        for s in strs {
            let (mut one_num, mut zero_num) = (0, 0);
            for c in s.chars() {
                match c {
                    '0' => zero_num += 1,
                    '1' => one_num += 1,
                    _ => (),
                }
            }
            for i in (zero_num..=m).rev() {
                for j in (one_num..=n).rev() {
                    dp[i][j] = dp[i][j].max(dp[i - zero_num][j - one_num] + 1);
                }
            }
        }
        dp[m][n]
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

# C

#define max(a, b) ((a) > (b) ? (a) : (b))

int findMaxForm(char** strs, int strsSize, int m, int n) {
    int dp[m + 1][n + 1];
    memset(dp, 0, sizeof (int ) * (m + 1) * (n + 1));
    for(int i = 0; i < strsSize; i++){
        // Count zeros and ones
        int count0 = 0;
        int count1 = 0;
        char *str = strs[i];
        while (*str != '\0'){
            if(*str == '0'){
                count0++;
            } else{
                count1++;
            }
            str++;
        }
        for(int j = m; j >= count0; j--){
            for(int k = n; k >= count1; k--){
                dp[j][k] = max(dp[j][k], dp[j - count0][k - count1] + 1);
            }
        }
    }
    return dp[m][n];
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

# C#

public class Solution
{
    public int FindMaxForm(string[] strs, int m, int n)
    {
        int[,] dp = new int[m + 1, n + 1];
        foreach (string str in strs)
        {
            int zero = 0, one = 0;
            foreach (char c in str)
            {
                if (c == '0') zero++;
                else one++;
            }
            for (int i = m; i >= zero; i--)
            {
                for (int j = n; j >= one; j--)
                {
                    dp[i, j] = Math.Max(dp[i, j], dp[i - zero, j - one] + 1);
                }
            }
        }
        return dp[m, n];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
Last updated:: 9/4/2025, 3:19:38 PM

← 15. Complete Knapsack Theory →

Copyright © 2025 keetcoder