keetcoder

# 115. Distinct Subsequences

LeetCode Problem Link (opens new window)

Given strings s and t, count the number of distinct subsequences of t that can be formed from s.

A subsequence of a string is a new string formed by deleting some (or none) of the characters without disturbing the relative positions of the remaining characters. (e.g., "ACE" is a subsequence of "ABCDE", but "AEC" is not).

The problem data guarantees that the answer fits within a 32-bit signed integer.

115. Distinct Subsequences Example

Constraints:

  • 0 <= s.length, t.length <= 1000
  • Both strings s and t consist of English letters only

# Approach

If this problem required continuous sequences rather than subsequences, we might consider using KMP.

This problem is somewhat easier than that in "72. Edit Distance" as this is essentially only concerned with the delete operation; there is no need to consider replacement or addition operations.

However, compared to 392. Is Subsequence (opens new window), this problem is more challenging. The two-pointer technique will not suffice here, so let's analyze it using the dynamic programming approach outlined in five steps:

  1. Define the dp array and its meaning

Define dp[i][j] as the number of ways to form the subsequence ending with the (i-1)th character of s that results in the subsequence ending with the (j-1)th character of t.

The reason for this definition (i-1, j-1) is thoroughly explained in 718. Maximum Length of Repeated Subarray (opens new window).

  1. Define the recurrence relation

For this kind of problem, there are typically two cases to analyze:

  • s[i - 1] is equal to t[j - 1]
  • s[i - 1] is not equal to t[j - 1]

When s[i - 1] is equal to t[j - 1], dp[i][j] can be formed in two ways.

One way is to use s[i - 1] for the matching. The number of such subsequences is dp[i - 1][j - 1]. This is because the matching has already included the last characters of both substrings s and t, so we only need dp[i-1][j-1].

Another way is to not use s[i - 1] for the matching, with the count being dp[i - 1][j].

Some might wonder why we should consider not using s[i - 1] for matching when the characters match.

For example, for s: "bagg" and t: "bag", s[3] matches t[2], but the string s can achieve the match without using s[3] by forming "bag" from s[0]s[1]s[2].

Alternatively, it can also use s[3] for the match, forming "bag" from s[0]s[1]s[3].

So when s[i - 1] is equal to t[j - 1], dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j].

When s[i - 1] is not equal to t[j - 1], we only count the case where s[i - 1] is not used for matching (simulating deleting this character from s). Thus, dp[i][j] = dp[i - 1][j].

Here, some might wonder why we don't consider "not using t[j - 1] for matching."

It's important to clarify that we are counting how many times t appears in s as a subsequence, not how many times s appears in t. So, we only consider the deletion cases from s, i.e., not using s[i - 1] for matching.

  1. Initializing the dp array

From the recurrence relations dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j] and dp[i][j] = dp[i - 1][j], we see that dp[i][j] is deduced from the above and top-left positions, as shown in the image. Thus, dp[i][0] and dp[0][j] need to be initialized.

Every time during initialization, it's essential to recall the definition of dp[i][j] and not to initialize based on instinct.

What does dp[i][0] represent?

dp[i][0] shows the number of ways the subsequence ending with i-1 in s can be transformed into an empty string t by potentially deleting all elements. Thus, dp[i][0] should always be 1, as the only way to obtain an empty string from i-1 characters of s is by deleting all of them.

Similarly, dp[0][j] means how many ways an empty subsequence of s can form a subsequence until j-1 in t. Therefore, dp[0][j] should be 0 because an empty subsequence cannot transform into any non-empty sequence.

For the special case, dp[0][0] should be 1 as an empty s can transform to an empty t without any operations.

Once the initialization is clear, the code is as follows:

vector<vector<long long>> dp(s.size() + 1, vector<long long>(t.size() + 1));
for (int i = 0; i <= s.size(); i++) dp[i][0] = 1;
for (int j = 1; j <= t.size(); j++) dp[0][j] = 0;
1
2
3
  1. Determining traversal order

The recursive relations dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j] and dp[i][j] = dp[i - 1][j] show that dp[i][j] is derived from the top-left and above positions.

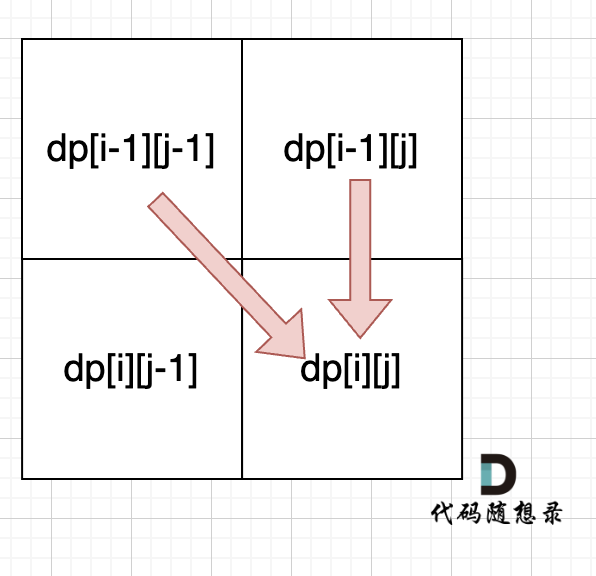
Thus, you must traverse from top to bottom and left to right to ensure that dp[i][j] can be computed from previously calculated values.

Here is the corresponding code:

for (int i = 1; i <= s.size(); i++) {
    for (int j = 1; j <= t.size(); j++) {
        if (s[i - 1] == t[j - 1]) {
            dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
        } else {
            dp[i][j] = dp[i - 1][j];
        }
    }
}
1
2
3
4
5
6
7
8
9
  1. Example to deduce the dp array

Consider s: "baegg" and t: "bag". The deduced dp array looks like this:

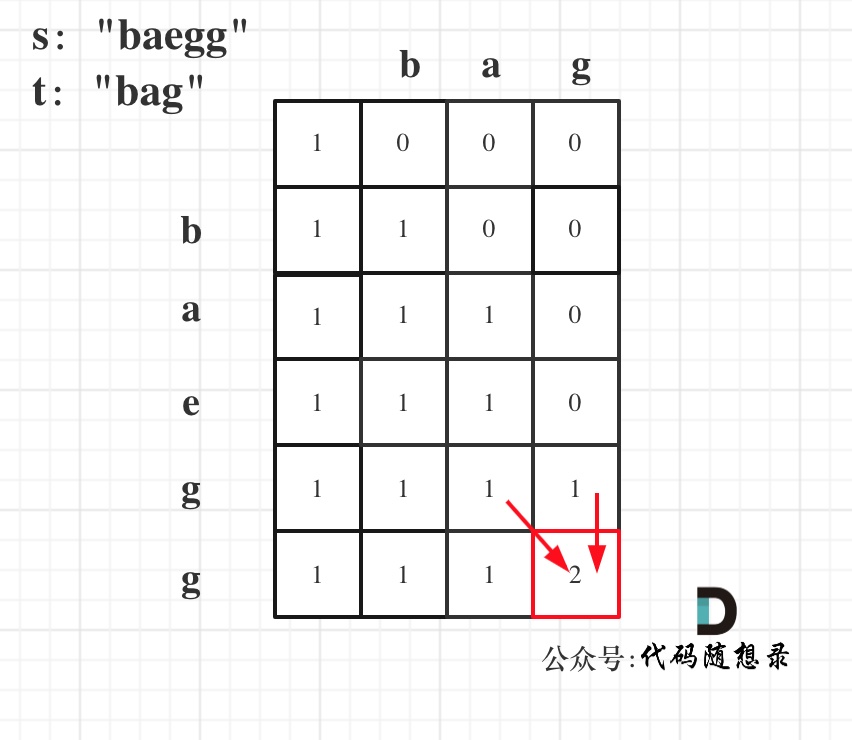
115. Distinct Subsequences

If your implemented code is not working as expected, try printing out the dp array to verify if it matches the expected pattern.

The five steps of dynamic programming are now complete, and here's the complete code:

class Solution {
public:
    int numDistinct(string s, string t) {
        vector<vector<uint64_t>> dp(s.size() + 1, vector<uint64_t>(t.size() + 1));
        for (int i = 0; i <= s.size(); i++) dp[i][0] = 1;
        for (int j = 1; j <= t.size(); j++) dp[0][j] = 0;
        for (int i = 1; i <= s.size(); i++) {
            for (int j = 1; j <= t.size(); j++) {
                if (s[i - 1] == t[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
                } else {
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        return dp[s.size()][t.size()];
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
  • Time Complexity: O(n * m)
  • Space Complexity: O(n * m)

# Other Language Versions

# Java:

class Solution {
    public int numDistinct(String s, String t) {
        int[][] dp = new int[s.length() + 1][t.length() + 1];
        for (int i = 0; i < s.length() + 1; i++) {
            dp[i][0] = 1;
        }
        
        for (int i = 1; i < s.length() + 1; i++) {
            for (int j = 1; j < t.length() + 1; j++) {
                if (s.charAt(i - 1) == t.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
                }else{
                    dp[i][j] = dp[i - 1][j];
                }
            }
        }
        
        return dp[s.length()][t.length()];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

# Python:

class Solution:
    def numDistinct(self, s: str, t: str) -> int:
        dp = [[0] * (len(t)+1) for _ in range(len(s)+1)]
        for i in range(len(s)):
            dp[i][0] = 1
        for j in range(1, len(t)):
            dp[0][j] = 0
        for i in range(1, len(s)+1):
            for j in range(1, len(t)+1):
                if s[i-1] == t[j-1]:
                    dp[i][j] = dp[i-1][j-1] + dp[i-1][j]
                else:
                    dp[i][j] = dp[i-1][j]
        return dp[-1][-1]
1
2
3
4
5
6
7
8
9
10
11
12
13
14

# Python3:

class SolutionDP2:
    """ 
    Since dp[i] only depends on the state of dp[i - 1],
    we can cache the state of dp[i - 1] to compress dp,
    which reduces the space complexity.
    (This is equivalent to a rolling array)
    """
    
    def numDistinct(self, s: str, t: str) -> int:
        n1, n2 = len(s), len(t)
        if n1 < n2:
            return 0

        dp = [0 for _ in range(n2 + 1)]
        dp[0] = 1

        for i in range(1, n1 + 1):
            # Must deepcopy
            # Otherwise, prev[i] and dp[i] refer to the same address
            prev = dp.copy()
            # Prune, ensuring the length of s is greater than or equal to t
            # Because for any i, i > n1, dp[i] = 0
            # No need to update the state. 
            end = i if i < n2 else n2
            for j in range(1, end + 1):
                if s[i - 1] == t[j - 1]:
                    dp[j] = prev[j - 1] + prev[j]
                else:
                    dp[j] = prev[j]
        return dp[-1]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

# Go:

func numDistinct(s string, t string) int {
    dp:= make([][]int,len(s)+1)
    for i:=0;i<len(dp);i++{
        dp[i] = make([]int,len(t)+1)
    }
    // Initialize
    for i:=0;i<len(dp);i++{
        dp[i][0] = 1
    }
    // dp[0][j] defaults to 0, no need for initialization
    for i:=1;i<len(dp);i++{
        for j:=1;j<len(dp[i]);j++{
            if s[i-1] == t[j-1]{
                dp[i][j] = dp[i-1][j-1] + dp[i-1][j]
            }else{
                dp[i][j] = dp[i-1][j]
            }
        }
    }
    return dp[len(dp)-1][len(dp[0])-1]
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

# JavaScript:

const numDistinct = (s, t) => {
    let dp = Array.from(Array(s.length + 1), () => Array(t.length +1).fill(0));

    for(let i = 0; i <=s.length; i++) {
        dp[i][0] = 1;
    }
    
    for(let i = 1; i <= s.length; i++) {
        for(let j = 1; j<= t.length; j++) {
            if(s[i-1] === t[j-1]) {
                dp[i][j] = dp[i-1][j-1] + dp[i-1][j];
            } else {
                dp[i][j] = dp[i-1][j]
            }
        }
    }

    return dp[s.length][t.length];
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

# TypeScript:

function numDistinct(s: string, t: string): number {
    /**
        dp[i][j]: number of distinct subsequences of t using the first i chars of s that form
                  the first j chars of t
        dp[0][0]=1, represents s being an empty string and t also being empty
     */
    const sLen: number = s.length,
        tLen: number = t.length;
    const dp: number[][] = new Array(sLen + 1).fill(0)
        .map(_ => new Array(tLen + 1).fill(0));
    for (let m = 0; m < sLen; m++) {
        dp[m][0] = 1;
    }
    for (let i = 1; i <= sLen; i++) {
        for (let j = 1; j <= tLen; j++) {
            if (s[i - 1] === t[j - 1]) {
                dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
            } else {
                dp[i][j] = dp[i - 1][j];
            }
        }
    }
    return dp[sLen][tLen];
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

# Rust:

impl Solution {
    pub fn num_distinct(s: String, t: String) -> i32 {
        if s.len() < t.len() {
            return 0;
        }
        let mut dp = vec![vec![0; s.len() + 1]; t.len() + 1];
        // i = 0, t is an empty string, number of ways s can be a subsequence is 1 (delete all elements of s)
        dp[0] = vec![1; s.len() + 1];
        for (i, char_t) in t.chars().enumerate() {
            for (j, char_s) in s.chars().enumerate() {
                if char_t == char_s {
                    // Number of subsequences of t's first i chars in s's first j chars
                    dp[i + 1][j + 1] = dp[i][j] + dp[i + 1][j];
                    continue;
                }
                dp[i + 1][j + 1] = dp[i + 1][j];
            }
        }
        dp[t.len()][s.len()]
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

Rolling Array

impl Solution {
    pub fn num_distinct(s: String, t: String) -> i32 {
        if s.len() < t.len() {
            return 0;
        }
        let (s, t) = (s.into_bytes(), t.into_bytes());
        // For t being an empty string, number of ways s can be a subsequence is 1 (delete all elements of s)
        let mut dp = vec![1; s.len() + 1];
        for char_t in t {
            // need to deepcopy
            let mut pre = dp[0];
            dp[0] = 0;
            for (j, &char_s) in s.iter().enumerate() {
                let temp = dp[j + 1];
                if char_t == char_s {
                    dp[j + 1] = pre + dp[j];
                } else {
                    dp[j + 1] = dp[j];
                }
                pre = temp;
            }
        }
        dp[s.len()]
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
Last updated:: 9/4/2025, 3:19:38 PM

← 42. Delete Operation for Two Strings →

Copyright © 2025 keetcoder