416. Partition Equal Subset Sum

LeetCode problem link (opens new window)

Difficulty: Medium

Given a non-empty array containing only positive integers, determine if you can partition the array into two subsets such that the sum of elements in both subsets is equal.

Note: Each element in the array will not exceed 100. The array size will not exceed 200.

Example 1:

• Input: [1, 5, 11, 5]
• Output: true
• Explanation: The array can be partitioned as [1, 5, 5] and [11].

Example 2:

• Input: [1, 2, 3, 5]
• Output: false
• Explanation: The array cannot be partitioned into two subsets with equal sum.

Constraints:

• 1 <= nums.length <= 200
• 1 <= nums[i] <= 100

Thought Process

At first glance, this problem is similar to the following two problems, which you can solve using backtracking:

• 698. Partition to K Equal Sum Subsets
• 473. Matchsticks to Square

The task is to determine if a subset exists in the array whose sum is equal to half of the total sum of the array.

Instead of using backtracking, which results in a solution timeout in the worst case, we can leverage a dynamic programming approach similar to the 0-1 Knapsack Problem.

This problem can be solved using a classic 0-1 knapsack algorithm.

For those unfamiliar with 0-1 knapsack, it is advisable to thoroughly go through the following resources:

• Knapsack Theory 01 Knapsack-1 (opens new window)
• Knapsack Theory 01 Knapsack-2 (opens new window)

0-1 Knapsack Problem

The 0-1 knapsack problem involves choosing items with given weights and values to include in a knapsack with a maximum weight capacity such that the total value of the items is maximized. Each item can only be used once.

Knapsack algorithms come in various types such as 0-1 knapsack, complete knapsack, multiple knapsack, grouped knapsack, and mixed knapsack.

Pay attention to the description of whether items can be placed in the knapsack more than once.

Since each item can only be used once in this problem, it is a 0-1 knapsack problem.

In essence, we want to see if a subset can fill a knapsack with half the sum of the array.

1. Define the DP Array and Its Meaning

In the 0-1 knapsack problem, dp[j] represents the maximum total value of a knapsack with a capacity of j.

If the knapsack is filled to capacity target, then dp[target] should be equal to target.

Using the input array [1, 5, 11, 5] as an example, dp[7] can only be 6, because it can only include 1 and 5.

However, dp[6] can be 6 with items 1 and 5, so if dp[6] == 6, the knapsack is filled.

2. Establish the Recurrence Relation

For the 0-1 knapsack, the recurrence relation is given by: dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

In this problem, the weight and value of each item are nums[i].

Therefore, the recurrence relation is: dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);

3. Initialize the DP Array

In the 0-1 knapsack problem, we previously covered how to initialize a 1D DP array.

Logically, dp[0] is always 0.

If the given value is positive and non-zero, all other elements can also be initialized to 0.

Since all elements in this problem are positive integers, initializing non-zero elements of the DP array to 0 suffices.

Here's the code:

// The problem specifies each element will not exceed 100, and the total size will not exceed 200.
// Therefore, the sum won't exceed 20000, and half of it (i.e., the knapsack size) can be up to 10001.
vector<int> dp(10001, 0);

4. Determine the Iteration Order

In Knapsack Theory 01 Knapsack-2 (opens new window), it is mentioned that when using a 1D DP array, iterating over items should be the outer loop, and iterating over the knapsack should be the inner loop, in reverse order.

Here's the code:

// Start the 0-1 knapsack
for(int i = 0; i < nums.size(); i++) {
    for(int j = target; j >= nums[i]; j--) { // Each item can only be used once, so iterate in reverse
        dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
    }
}

5. Example to Derive the DP Array

The value of dp[j] should always be less than or equal to j.

If dp[j] == j, it indicates that a subset with the total sum of j has been achieved, which is critical to understand.

Using example 1, input [1, 5, 11, 5], as illustrated:

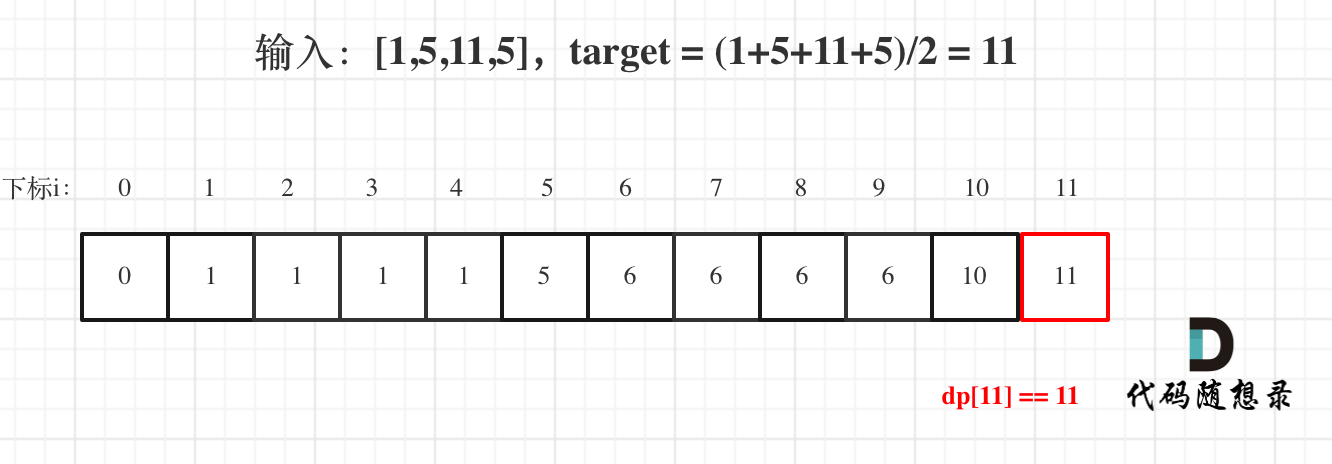
In the end, dp[11] == 11, indicating the array can be partitioned into two subsets with equal sum.

After this analysis, here’s the C++ solution:

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int sum = 0;

        // dp[i] where i represents the total sum in the knapsack
        // As stated in the problem: each element will not exceed 100, the array size will not exceed 200
        // The total sum will not exceed 20000, so half of it is enough to consider
        vector<int> dp(10001, 0);
        for (int i = 0; i < nums.size(); i++) {
            sum += nums[i];
        }
        // Alternatively, the sum can be calculated using a built-in function
        // int sum = accumulate(nums.begin(), nums.end(), 0);
        if (sum % 2 == 1) return false;
        int target = sum / 2;

        // Start the 0-1 knapsack
        for(int i = 0; i < nums.size(); i++) {
            for(int j = target; j >= nums[i]; j--) { // Each item can only be used once, so iterate in reverse
                dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
            }
        }
        // If a subset with total sum target has been found
        if (dp[target] == target) return true;
        return false;
    }
};

• Time Complexity: O(n^2)
• Space Complexity: O(n), although dp array size is a constant, it is a big constant.

Conclusion

This problem is a classic application of the 0-1 knapsack problem, requiring dissection of the problem to recognize the use of the knapsack algorithm.

Recognize: In this problem, the items are nums[i], the weight of the item is nums[i], the value is also nums[i], and the knapsack size to be filled is sum/2.

Upon completing this problem, it's crucial to clearly understand: knapsack problems aren't limited to finding the maximum value but also determine whether it's possible to fill the knapsack.

Other Language Versions

Java:

class Solution {
    public boolean canPartition(int[] nums) {
        if(nums == null || nums.length == 0) return false;
        int n = nums.length;
        int sum = 0;
        for(int num : nums) {
            sum += num;
        }
        // If the total sum is odd, it cannot be partitioned equally
        if(sum % 2 != 0) return false;
        int target = sum / 2;
        int[] dp = new int[target + 1];
        for(int i = 0; i < n; i++) {
            for(int j = target; j >= nums[i]; j--) {
                // The weight of item i is nums[i], which is also its value
                dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);
            }
           
            // Slight optimization: Check if dp[target] == target immediately after each inner loop to improve time complexity (26ms -> 20ms)
            if(dp[target] == target)
                return true;
        }
        return dp[target] == target;
    }
}

2D Array Version (easier to understand):

public class Solution {
    public static void main(String[] args) {
        int num[] = {1,5,11,5};
        canPartition(num);

    }
    public static boolean canPartition(int[] nums) {
        int len = nums.length;
        // The problem states a non-empty array, so we can skip checking for empty arrays
        int sum = 0;
        for (int num : nums) {
            sum += num;
        }
        // Special case: If the sum is odd, partitioning is impossible
        if ((sum %2 ) != 0) {
            return false;
        }

        int target = sum / 2; // Target knapsack capacity
        // Create a 2D state array, rows: item index, columns: capacity (including 0)
        /*
        dp[i][j] represents selecting some positive integers from the subarray [0, i]
        Each number can be used once to make their sum exactly equal to j.
        */
        boolean[][] dp = new boolean[len][target + 1];

        // Fill the first row: The first item can fill the knapsack with its own weight (if dp[][] array definition is "exactly," items with larger capacities should not be considered)
        if (nums[0] <= target) {
            dp[0][nums[0]] = true;
        }
        // Fill the subsequent rows
        // Outer loop iterates over items
        for (int i = 1; i < len; i++) {
            // Inner loop iterates over the knapsack
            for (int j = 0; j <= target; j++) {
                // First copy results from the previous row and adjust them
                dp[i][j] = dp[i - 1][j];

                // If an item's weight is exactly equal to the knapsack's capacity, it matches the dp array definition too
                if (nums[i] == j) {
                    dp[i][j] = true;
                    continue;
                }
                // If an item's weight is less than j, consider if it can fit in the knapsack
                // dp[i - 1][j] means the item is not included in the knapsack. If there's a subset in [0, i - 1] with a sum of j, then dp[i][j] = true;
                // dp[i - 1][j - nums[i]] means including the item in the knapsack. Find a subset in [0, i - 1] with a sum of j - nums[i].
                if (nums[i] < j) {
                    dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i]];
                }
            }
        }
        for (int i = 0; i < len; i++) {
            for (int j = 0; j <= target; j++) {
                System.out.print(dp[i][j]+" ");
            }
            System.out.println();
        }
        return dp[len - 1][target];
    }
}
// dp array output
false true false false false false false false false false false false 
false true false false false true true false false false false false 
false true false false false true true false false false false true 
false true false false false true true false false false true true 

Two-Dimensional Array Integer Version

class Solution {
    public boolean canPartition(int[] nums) {
        //using 2-D DP array.
        int len = nums.length;
        //check edge cases;
        if(len == 0)
            return false;

        int sum = 0;
        for (int num : nums)
            sum += num;
        //we only deal with even numbers. If sum is odd, return false;
        if(sum % 2 == 1)
            return false;
        
        int target = sum / 2;
        int[][] dp = new int[nums.length][target + 1];

        // for(int j = 0; j <= target; j++){
        //     if(j < nums[0])
        //         dp[0][j] = 0;
        //     else
        //         dp[0][j] = nums[0];
        // }

        //initialize dp array
        for(int j = nums[0]; j <= target; j++){
            dp[0][j] = nums[0];
        }

        for(int i = 1; i < len; i++){
            for(int j = 0; j <= target; j++){
                if (j < nums[i]) 
                    dp[i][j] = dp[i - 1][j];
                else 
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - nums[i]] + nums[i]);
            }
        }

        //print out DP array
        // for(int x : dp){
        //     System.out.print(x + ",");
        // }
        // System.out.print("    "+i+" row"+"\n");
        return dp[len - 1][target] == target;
    }
}
//dp array output for test case 1.
0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 
0, 1, 1, 1, 1, 5, 6, 6, 6, 6, 6, 6, 
0, 1, 1, 1, 1, 5, 6, 6, 6, 6, 6, 11, 
0, 1, 1, 1, 1, 5, 6, 6, 6, 6, 10, 11, 

Python:

Carl's Version

class Solution:
    def canPartition(self, nums: List[int]) -> bool:
        _sum = 0

        # dp[i] where i represents the total sum in the knapsack
        # As stated in the problem: each element will not exceed 100, the array size will not exceed 200
        # The total sum will not exceed 20000, so half of it is enough to consider
        dp = [0] * 10001
        for num in nums:
            _sum += num
        # Alternatively, the sum can be calculated using a built-in function
        # _sum = sum(nums)
        if _sum % 2 == 1:
            return False
        target = _sum // 2

        # Start the 0-1 knapsack
        for num in nums:
            for j in range(target, num - 1, -1):  # Each item can only be used once, so iterate in reverse
                dp[j] = max(dp[j], dp[j - num] + num)

        # If a subset with total sum target has been found
        if dp[target] == target:
            return True
        return False

Carl's Version (Simplified)

class Solution:
    def canPartition(self, nums: List[int]) -> bool:
        if sum(nums) % 2 != 0:
            return False
        target = sum(nums) // 2
        dp = [0] * (target + 1)
        for num in nums:
            for j in range(target, num-1, -1):
                dp[j] = max(dp[j], dp[j-num] + num)
        return dp[-1] == target

2D DP Version

class Solution:
    def canPartition(self, nums: List[int]) -> bool:
        
        total_sum = sum(nums)

        if total_sum % 2 != 0:
            return False

        target_sum = total_sum // 2
        dp = [[False] * (target_sum + 1) for _ in range(len(nums) + 1)]

        # Initialize first row (an empty subset can achieve a sum of 0)
        for i in range(len(nums) + 1):
            dp[i][0] = True

        for i in range(1, len(nums) + 1):
            for j in range(1, target_sum + 1):
                if j < nums[i - 1]:
                    # When the current number is greater than the target, it cannot be used
                    dp[i][j] = dp[i - 1][j]
                else:
                    # When the current number is less than or equal to the target, it can be chosen or skipped
                    dp[i][j] = dp[i - 1][j] or dp[i - 1][j - nums[i - 1]]

        return dp[len(nums)][target_sum]

1D DP Version

class Solution:
    def canPartition(self, nums: List[int]) -> bool:

        total_sum = sum(nums)

        if total_sum % 2 != 0:
            return False

        target_sum = total_sum // 2
        dp = [False] * (target_sum + 1)
        dp[0] = True

        for num in nums:
            # Iterate backward from target_sum to num with a step size of -1
            for i in range(target_sum, num - 1, -1):
                dp[i] = dp[i] or dp[i - num]
        return dp[target_sum]

 

Go:

1D DP

// Knapsack Theory 01 Knapsack-1 using Dynamic Programming
// Time Complexity: O(n^2), Space Complexity: O(n)
func canPartition(nums []int) bool {
    sum := 0
    for _, num := range nums {
        sum += num
    }
    // If the total sum is odd, it cannot be partitioned equally
    if sum % 2 == 1 {
        return false
    }
    
    target := sum / 2
    dp := make([]int, target + 1)

    for _, num := range nums {
        for j := target; j >= num; j-- {
            if dp[j] < dp[j - num] + num {
                dp[j] = dp[j - num] + num
            }
        }
    }
    return dp[target] == target
}

2D DP

func canPartition(nums []int) bool {
    sum := nums.sum()
    if sum % 2 == 1 {
        return false
    }
    target := sum / 2
    dp := make([][]int, len(nums))
    for i := range dp {
        dp[i] = make([]int, target + 1)
    }
    for j := nums[0]; j <= target; j++ {
        dp[0][j] = nums[0]
    }
    for i := 1; i < len(nums); i++ {
        for j := 0; j <= target; j++ {
            if j < nums[i] {
                dp[i][j] = dp[i-1][j]
            } else {
                dp[i][j] = max(dp[i-1][j], dp[i-1][j-nums[i]] + nums[i])
            }
        }  
    }
    return dp[len(nums)-1][target] == target
}

func max(x, y int) int {
    if x > y {
        return x
    }
    return y
}

JavaScript:

var canPartition = function(nums) {
    const sum = (nums.reduce((p, v) => p + v));
    if (sum & 1) return false;
    const dp = Array(sum / 2 + 1).fill(0);
    for(let i = 0; i < nums.length; i++) {
        for(let j = sum / 2; j >= nums[i]; j--) {
            dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);
            if (dp[j] === sum / 2) {
                return true;
            }
        }
    }
    return dp[sum / 2] === sum / 2;
};

Rust:

impl Solution {
    pub fn canPartition(nums: Vec<i32>) -> bool {
        let sum = nums.iter().sum::<i32>() as usize;
        if sum % 2 == 1 {
            return false;
        }
        let target = sum / 2;
        let mut dp = vec![0; target + 1];
        for n in nums {
            for j in (n as usize..=target).rev() {
                dp[j] = dp[j].max(dp[j - n as usize] + n)
            }
        }
        if dp[target] == target as i32 {
            return true;
        }
        false
    }
}

C:

2D DP:

/**
1. Meaning of dp array: dp[i][j] represents the maximum total value of the knapsack with capacity j.
2. Recurrence formula: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - nums[i]] + nums[i])
3. Initialization: Set dp[i][0] to 0. Because when knapsack capacity is 0, no elements can be put in. Set dp[0][j] = nums[0], when j >= nums[0] && j < target.
4. Iteration order: Items first, then knapsack.
*/
#define MAX(a, b) (((a) > (b)) ? (a) : (b))

int getSum(int* nums, int numsSize) {
    int sum = 0;

    int i;
    for(i = 0; i < numsSize; ++i) {
        sum += nums[i];
    }
    return sum;
}

bool canPartition(int* nums, int numsSize){
    // Calculate the total sum of elements
    int sum = getSum(nums, numsSize);
    // If the total sum is odd, even division into two equal subsets is impossible
    if(sum % 2)
        return false;

    // If a subset with a sum equal to target is found, nums can be partitioned
    int target = sum / 2;
    // Initialize dp array
    int dp[numsSize][target + 1];
    // Set dp[j][0] to 0. Because when knapsack capacity is 0, no elements can be put in.
    memset(dp, 0, sizeof(int) * numsSize * (target + 1));

    int i, j;
    // When knapsack capacity j is larger than nums[0], item nums[0] can be put in the dp[0][j]
    for(j = nums[0]; j <= target; ++j) {
        dp[0][j] = nums[0];
    }

    for(i = 1; i < numsSize; ++i) {
        for(j = 1; j <= target; ++j) {
            // If the current knapsack capacity j is less than nums[i], its value is equal to when considering items 0 to i-1
            if(j < nums[i])
                dp[i][j] = dp[i - 1][j];
            // Otherwise, knapsack capacity equals the max value between putting in num[i] or not
            else
                dp[i][j] = MAX(dp[i - 1][j], dp[i - 1][j  - nums[i]] + nums[i]);
        }
    }
    // Check if the knapsack is filled to capacity with a total value equal to target
    return dp[numsSize - 1][target] == target;
}

Rolling Array:

/**
1. Meaning of dp array: dp[j] is the maximum total value of a knapsack with capacity j.
2. Recurrence formula: dp[j] = max(dp[j], dp[j - nums[i]] + nums[i])
3. Initialization: All elements can be initialized to 0
4. Iteration order: Items first, then knapsack
*/
#define MAX(a, b) (((a) > (b)) ? (a) : (b))

int getSum(int* nums, int numsSize) {
    int sum = 0;

    int i;
    for(i = 0; i < numsSize; ++i) {
        sum += nums[i];
    }
    return sum;
}

bool canPartition(int* nums, int numsSize){
    // Calculate the total sum of elements
    int sum = getSum(nums, numsSize);
    // If the total sum is odd, even division into two equal subsets is impossible
    if(sum % 2)
        return false;
    // Capacity of the knapsack
    int target = sum / 2;

    // Initialize the dp array, with all elements set to 0
    int dp[target + 1];
    memset(dp, 0, sizeof(int) * (target + 1));

    int i, j;
    // Iterate over items and then the knapsack
    for(i = 0; i < numsSize; ++i) {
        for(j = target; j >= nums[i]; --j) {
            dp[j] = MAX(dp[j], dp[j - nums[i]] + nums[i]);
        }
    }
    
    // Check if the knapsack is filled to capacity
    return dp[target] == target;
}

TypeScript:

1D Array, concise

function canPartition(nums: number[]): boolean {
    const sum: number = nums.reduce((pre, cur) => pre + cur);
    if (sum % 2 === 1) return false;
    const bagSize: number = sum / 2;
    const goodsNum: number = nums.length;
    const dp: number[] = new Array(bagSize + 1).fill(0);
    for (let i = 0; i < goodsNum; i++) {
        for (let j = bagSize; j >= nums[i]; j--) {
            dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);
        }
    }
    return dp[bagSize] === bagSize;
};

2D Array, easier to understand

function canPartition(nums: number[]): boolean {
    /**
        weightArr = nums;
        valueArr = nums;
        bagSize = sum / 2; (sum is the total sum of nums elements);
        Process it as a 0-1 knapsack
     */
    const sum: number = nums.reduce((pre, cur) => pre + cur);
    if (sum % 2 === 1) return false;
    const bagSize: number = sum / 2;
    const weightArr: number[] = nums;
    const valueArr: number[] = nums;
    const goodsNum: number = weightArr.length;
    const dp: number[][] = new Array(goodsNum)
    	.fill(0)
    	.map(_ => new Array(bagSize + 1).fill(0));
    for (let i = weightArr[0]; i <= bagSize; i++) {
        dp[0][i] = valueArr[0];
    }
    for (let i = 1; i < goodsNum; i++) {
        for (let j = 0; j <= bagSize; j++) {
            if (j < weightArr[i]) {
                dp[i][j] = dp[i - 1][j];
            } else {
                dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weightArr[i]] + valueArr[i]);
            }
        }
    }
    return dp[goodsNum - 1][bagSize] === bagSize;
};

Scala:

Rolling Array:

object Solution {
  def canPartition(nums: Array[Int]): Boolean = {
    var sum = nums.sum
    if (sum % 2 != 0) return false
    var half = sum / 2
    var dp = new Array[Int](half + 1)

    // Iterate
    for (i <- 0 until nums.length; j <- half to nums(i) by -1) {
      dp(j) = math.max(dp(j), dp(j - nums(i)) + nums(i))
    }

    if (dp(half) == half) true else false
  }
}

2D Array:

object Solution {
  def canPartition(nums: Array[Int]): Boolean = {
    var sum = nums.sum
    if (sum % 2 != 0) return false
    var half = sum / 2
    var dp = Array.ofDim[Int](nums.length, half + 1)
    
    // Initialization
    for (j <- nums(0) to half) dp(0)(j) = nums(0)

    // Iterate
    for (i <- 1 until nums.length; j <- 1 to half) {
      if (j - nums(i) >= 0) dp(i)(j) = nums(i) + dp(i - 1)(j - nums(i))
      dp(i)(j) = math.max(dp(i)(j), dp(i - 1)(j))
    }
    
    // Return true if equal to half, otherwise false
    if (dp(nums.length - 1)(half) == half) true else false
  }
}

C#

public class Solution
{
    public bool CanPartition(int[] nums)
    {
        int sum = 0;
        int[] dp = new int[10001];
        foreach (int num in nums)
        {
            sum += num;
        }
        if (sum % 2 == 1) return false;
        int tartget = sum / 2;
        for (int i = 0; i < nums.Length; i++)
        {
            for (int j = tartget; j >= nums[i]; j--)
            {
                dp[j] = Math.Max(dp[j], dp[j - nums[i]] + nums[i]);
            }
        }
        if (dp[tartget] == tartget)
            return true;

        return false;

    }
}