# 188. Best Time to Buy and Sell Stock IV
LeetCode Problem Link (opens new window)
You are given an integer array prices where prices[i] is the price of a given stock on the ith day.
Design an algorithm to compute the maximum profit you can achieve. You may complete at most k transactions.
Note: You may not engage in multiple transactions simultaneously (i.e., you must sell the stock before you buy again).
Example 1:
Input:
k = 2, prices = [2,4,1]Output:
2Explanation: Buy on day 1 (stock price = 2) and sell on day 2 (stock price = 4), profit = 4-2 = 2.Example 2:
Input:
k = 2, prices = [3,2,6,5,0,3]Output:
7Explanation: Buy on day 2 (stock price = 2) and sell on day 3 (stock price = 6), profit = 6-2 = 4. Then buy on day 5 (stock price = 0) and sell on day 6 (stock price = 3), profit = 3-0 = 3.
Constraints:
0 <= k <= 1000 <= prices.length <= 10000 <= prices[i] <= 1000
# Approach
This problem can be seen as an advanced version of 0123.Best Time to Buy and Sell Stock III (opens new window), where at most k transactions are allowed.
Let's analyze it according to the dynamic programming five-step method:
- Define the dp array and its meaning
In 0123.Best Time to Buy and Sell Stock III (opens new window), a two-dimensional dp array was used, and it is the same for this problem.
Use a two-dimensional array dp[i][j]: the maximum cash left after ith day when the state is j is dp[i][j].
The state j represents:
- 0 means no operation
- 1 means the first buy
- 2 means the first sell
- 3 means the second buy
- 4 means the second sell
- .....
Notice the pattern: except for 0, odd numbers mean buying, and even numbers mean selling.
The problem asks for at most k transactions, so the range for j can be defined as 2 * k + 1.
Thus, the C++ definition for the two-dimensional dp array is:
vector<vector<int>> dp(prices.size(), vector<int>(2 * k + 1, 0));
- Determine the recursive formula
Remember: dp[i][1] indicates the buying state on the ith day, not necessarily that you must buy on the ith day.
To achieve the state dp[i][1], there are two operations:
- Operation 1: Buy stock on the
ith day, sodp[i][1] = dp[i - 1][0] - prices[i] - Operation 2: Do nothing on the
ith day and inherit the buy status from the day before, i.e.,dp[i][1] = dp[i - 1][1]
Choose the maximum, so dp[i][1] = max(dp[i - 1][0] - prices[i], dp[i - 1][1]);
Similarly, for dp[i][2], we have two operations:
- Operation 1: Sell stock on the
ith day, sodp[i][2] = dp[i - 1][1] + prices[i] - Operation 2: Do nothing on the
ith day and inherit the sell status from the day before, i.e.,dp[i][2] = dp[i - 1][2]
So dp[i][2] = max(dp[i - 1][1] + prices[i], dp[i - 1][2]);
Similarly, you can generalize the remaining states, with the code as follows:
for (int j = 0; j < 2 * k - 1; j += 2) {
dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);
dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
}
2
3
4
The main difference between this problem and 0123.Best Time to Buy and Sell Stock III (opens new window) is here. You need to consider the states where j is odd for buying and even for selling.
- Initialize the dp array
On day 0, do nothing; this is the easiest to think of, which is 0, i.e., dp[0][0] = 0;
On day 0, do the first buy operation; dp[0][1] = -prices[0];
What should the initial value be for doing the first sell operation on day 0?
At this point, you haven’t bought yet, so how can you sell? You can interpret it as buying and selling on the same day, so dp[0][2] = 0;
What should the initial value be for the second buy operation on day 0? Some might be confused since you haven’t even done the first buy, so how to initialize the second buy?
The second buy relies on the first sell state. Essentially, it means that on day 0, the first buy and first sell happened, then a second buy (second time), so you don’t have cash on hand, so buying reduces your cash accordingly.
Therefore, the second buy's initial value should be: dp[0][3] = -prices[0];
Second sell initialization: dp[0][4] = 0;
So similarly, you can conclude that when j is odd in dp[0][j], they are all initialized as -prices[0].
The code is as follows:
for (int j = 1; j < 2 * k; j += 2) {
dp[0][j] = -prices[0];
}
2
3
In the initialization part, you still need to keep in mind the odd indices for buys and even for sells.
- Determine the traversal order
From the recurrence relation, it is evident that you must traverse from front to back because dp[i] relies on the values of dp[i - 1].
- Example to derive the dp array
Take the input [1,2,3,4,5], k=2 as an example.
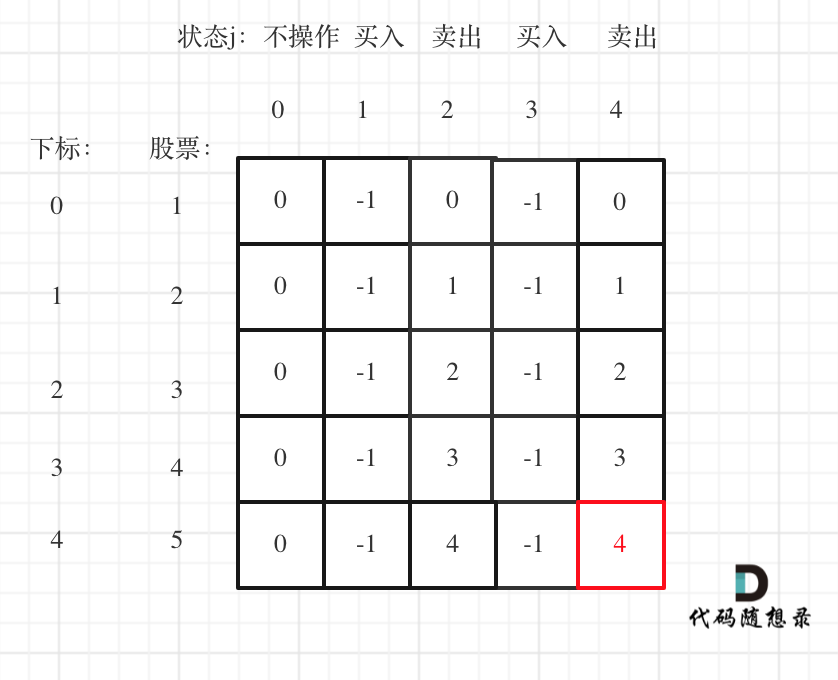
The last sell is always the maximum profit, so dp[prices.size() - 1][2 * k] in red is the solution.
With the above analysis, the C++ code is as follows:
class Solution {
public:
int maxProfit(int k, vector<int>& prices) {
if (prices.size() == 0) return 0;
vector<vector<int>> dp(prices.size(), vector<int>(2 * k + 1, 0));
for (int j = 1; j < 2 * k; j += 2) {
dp[0][j] = -prices[0];
}
for (int i = 1;i < prices.size(); i++) {
for (int j = 0; j < 2 * k - 1; j += 2) {
dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);
dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
}
}
return dp[prices.size() - 1][2 * k];
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
- Time complexity: O(n * k), where n is the length of
prices. - Space complexity: O(n * k).
Some solutions define a three-dimensional array dp[i][j][k], where i is the day, j is the number of transactions, k represents whether the state is buy or sell, which is intuitive from the definition.
But it feels a little cumbersome to operate a three-dimensional array. I use a two-dimensional array to simulate the situation of a three-dimensional array, making the code look cleaner.
# Other Language Versions
# Java:
// Version One: Three-Dimensional dp Array
class Solution {
public int maxProfit(int k, int[] prices) {
if (prices.length == 0) return 0;
// [Number of days][Number of transactions][Stock holding status]
int len = prices.length;
int[][][] dp = new int[len][k + 1][2];
// dp array initialization
// Initialize all the transaction times to ensure the final result is the maximum profit after at most k transactions
for (int i = 0; i <= k; i++) {
dp[0][i][1] = -prices[0];
}
for (int i = 1; i < len; i++) {
for (int j = 1; j <= k; j++) {
// dp equation, 0 means not holding/selling, 1 means holding/buying
dp[i][j][0] = Math.max(dp[i - 1][j][0], dp[i - 1][j][1] + prices[i]);
dp[i][j][1] = Math.max(dp[i - 1][j][1], dp[i - 1][j - 1][0] - prices[i]);
}
}
return dp[len - 1][k][0];
}
}
// Version Two: Two-Dimensional dp Array
class Solution {
public int maxProfit(int k, int[] prices) {
if (prices.length == 0) return 0;
// [Number of days][Stock state]
// Stock states: odd numbers mean holding/buying in the k-th transaction, even numbers mean not holding/selling in the k-th transaction, 0 means no operation
int len = prices.length;
int[][] dp = new int[len][k*2 + 1];
// dp array initialization, same as Version One
for (int i = 1; i < k*2; i += 2) {
dp[0][i] = -prices[0];
}
for (int i = 1; i < len; i++) {
for (int j = 0; j < k*2 - 1; j += 2) {
dp[i][j + 1] = Math.max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);
dp[i][j + 2] = Math.max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
}
}
return dp[len - 1][k*2];
}
}
// Version Three: One-Dimensional dp Array
class Solution {
public int maxProfit(int k, int[] prices) {
if(prices.length == 0){
return 0;
}
if(k == 0){
return 0;
}
// Essentially this is an extension of problem 123; you only need to keep track of 2 transactions' states
// Here, we track states for k transactions
// Each transaction has both buy and sell states, so multiply by 2
int[] dp = new int[2 * k];
// Initialize, following the solution format for problem 123
for(int i = 0; i < dp.length / 2; i++){
dp[i * 2] = -prices[0];
}
for(int i = 1; i <= prices.length; i++){
dp[0] = Math.max(dp[0], -prices[i - 1]);
dp[1] = Math.max(dp[1], dp[0] + prices[i - 1]);
// Compare it with problem 123
for(int j = 2; j < dp.length; j += 2){
dp[j] = Math.max(dp[j], dp[j - 1] - prices[i-1]);
dp[j + 1] = Math.max(dp[j + 1], dp[j] + prices[i - 1]);
}
}
// Return the result of the last sell state
return dp[dp.length - 1];
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
class Solution {
public int maxProfit(int k, int[] prices) {
//edge cases
if(prices.length == 0 || k == 0)
return 0;
int dp[] = new int [k * 2 + 1];
// Logical same as above, initializing only odd states as we buy on odd days.
for(int i = 1; i < 2 * k + 1; i += 2){
dp[i] = -prices[0];
}
for(int i = 1; i < prices.length; i++){
for(int j = 1; j < 2 * k + 1; j++){
// Buy on odd days
if(j % 2 == 1)
dp[j] = Math.max(dp[j], dp[j - 1] - prices[i]);
// Sell on even days
else
dp[j] = Math.max(dp[j], dp[j - 1] + prices[i]);
}
// Print DP array
// for(int x : dp)
// System.out.print(x +", ");
// System.out.println();
}
// Return the profit from the 2*k-th sell.
return dp[2 * k];
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# Python:
Version One
class Solution:
def maxProfit(self, k: int, prices: List[int]) -> int:
if len(prices) == 0:
return 0
dp = [[0] * (2*k+1) for _ in range(len(prices))]
for j in range(1, 2*k, 2):
dp[0][j] = -prices[0]
for i in range(1, len(prices)):
for j in range(0, 2*k-1, 2):
dp[i][j+1] = max(dp[i-1][j+1], dp[i-1][j] - prices[i])
dp[i][j+2] = max(dp[i-1][j+2], dp[i-1][j+1] + prices[i])
return dp[-1][2*k]
2
3
4
5
6
7
8
9
10
11
12
Version Two
class Solution:
def maxProfit(self, k: int, prices: List[int]) -> int:
if len(prices) == 0: return 0
dp = [0] * (2*k + 1)
for i in range(1,2*k,2):
dp[i] = -prices[0]
for i in range(1,len(prices)):
for j in range(1,2*k + 1):
if j % 2:
dp[j] = max(dp[j],dp[j-1]-prices[i])
else:
dp[j] = max(dp[j],dp[j-1]+prices[i])
return dp[2*k]
2
3
4
5
6
7
8
9
10
11
12
13
Version Three: One-Dimensional dp Array (Easier to Understand)
class Solution:
def maxProfit(self, k: int, prices: List[int]) -> int:
dp = [0] * k * 2
for i in range(k):
dp[i * 2] = -prices[0]
for price in prices[1:]:
dc = dp.copy() # This is crucial, preserve the dp state of the previous day to avoid being overwritten
for i in range(2 * k):
if i % 2 == 1:
dp[i] = max(dc[i], dc[i - 1] + price)
else:
pre = 0 if i == 0 else dc[i - 1]
dp[i] = max(dc[i], pre - price)
return dp[-1]
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# Go:
Version One:
// Best Time to Buy and Sell Stock IV with Dynamic Programming
// Time complexity O(kn), Space complexity O(kn)
func maxProfit(k int, prices []int) int {
if k == 0 || len(prices) == 0 {
return 0
}
dp := make([][]int, len(prices))
status := make([]int, (2 * k + 1) * len(prices))
for i := range dp {
dp[i] = status[:2 * k + 1]
status = status[2 * k + 1:]
}
for j := 1; j < 2 * k; j += 2 {
dp[0][j] = -prices[0]
}
for i := 1; i < len(prices); i++ {
for j := 0; j < 2 * k; j += 2 {
dp[i][j+1] = max(dp[i-1][j+1], dp[i-1][j] - prices[i])
dp[i][j+2] = max(dp[i-1][j+2], dp[i-1][j+1] + prices[i])
}
}
return dp[len(prices) - 1][2 * k]
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
Version Two: Three-Dimensional dp Array
func maxProfit(k int, prices []int) int {
length := len(prices)
if length == 0 {
return 0
}
// [Days][Number of transactions][Holding status]
// 1 denotes not holding/selling, 0 denotes holding/buying
dp := make([][][]int, length)
for i := 0; i < length; i++ {
dp[i] = make([][]int, k+1)
for j := 0; j <= k; j++ {
dp[i][j] = make([]int, 2)
}
}
for j := 0; j <= k; j++ {
dp[0][j][0] = -prices[0]
}
for i := 1; i < length; i++ {
for j := 1; j <= k; j++ {
dp[i][j][0] = max188(dp[i-1][j][0], dp[i-1][j-1][1]-prices[i])
dp[i][j][1] = max188(dp[i-1][j][1], dp[i-1][j][0]+prices[i])
}
}
return dp[length-1][k][1]
}
func max188(a, b int) int {
if a > b {
return a
}
return b
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
Version Three: Space Optimization Version
func maxProfit(k int, prices []int) int {
n := len(prices)
// k transactions, 2 * k states
// States start from 1 to avoid checks
// Odd: holding (keep or buy)
// Even: not holding (keep or sell)
dp := make([][]int, 2)
dp[0] = make([]int, k * 2 + 1)
dp[1] = make([]int, k * 2 + 1)
// Initialize buy states
for i := 1; i <= k * 2; i += 2 {
dp[0][i] = -prices[0]
}
for i := 1; i < len(prices); i++ {
for j := 1; j <= k * 2; j++ {
if j % 2 == 1 {
dp[i % 2][j] = max(dp[(i - 1) % 2][j], dp[(i - 1) % 2][j - 1] - prices[i])
} else {
dp[i % 2][j] = max(dp[(i - 1) % 2][j], dp[(i - 1) % 2][j - 1] + prices[i])
}
}
}
return dp[(n - 1) % 2][k * 2]
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
Version Four: One-Dimensional dp Array (Easier to Understand)
func maxProfit(k int, prices []int) int {
dp := make([]int, 2 * k)
for i := range k {
dp[i * 2] = -prices[0]
}
for j := 1; j < len(prices); j++ {
dc := slices.Clone(dp) // This is the key, preserve the state of the previous day to avoid being overwritten
for i := range k * 2 {
if i % 2 == 1 {
dp[i] = max(dc[i], dc[i - 1] + prices[j])
} else {
pre := 0; if i >= 1 { pre = dc[i - 1] }
dp[i] = max(dc[i], pre - prices[j])
}
}
}
return dp[2 * k - 1]
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# JavaScript:
// Method 1: Dynamic Programming
const maxProfit = (k,prices) => {
if (prices == null || prices.length < 2 || k == 0) {
return 0;
}
let dp = Array.from(Array(prices.length), () => Array(2*k+1).fill(0));
for (let j = 1; j < 2 * k; j += 2) {
dp[0][j] = 0 - prices[0];
}
for(let i = 1; i < prices.length; i++) {
for (let j = 0; j < 2 * k; j += 2) {
dp[i][j+1] = Math.max(dp[i-1][j+1], dp[i-1][j] - prices[i]);
dp[i][j+2] = Math.max(dp[i-1][j+2], dp[i-1][j+1] + prices[i]);
}
}
return dp[prices.length - 1][2 * k];
};
// Method 2: Dynamic Programming + Space Optimization
var maxProfit = function(k, prices) {
let n = prices.length;
let dp = new Array(2*k+1).fill(0);
// dp buy states initialization
for (let i = 1; i <= 2*k; i += 2) {
dp[i] = - prices[0];
}
for (let i = 1; i < n; i++) {
for (let j = 1; j < 2*k+1; j++) {
// j is odd: buy state
if (j % 2) {
dp[j] = Math.max(dp[j], dp[j-1] - prices[i]);
} else {
// j is even: sell state
dp[j] = Math.max(dp[j], dp[j-1] + prices[i]);
}
}
}
return dp[2*k];
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
# TypeScript:
function maxProfit(k: number, prices: number[]): number {
const length: number = prices.length;
if (length === 0) return 0;
const dp: number[][] = new Array(length).fill(0)
.map(_ => new Array(k * 2 + 1).fill(0));
for (let i = 1; i <= k; i++) {
dp[0][i * 2 - 1] = -prices[0];
}
for (let i = 1; i < length; i++) {
for (let j = 1; j < 2 * k + 1; j++) {
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - 1] + Math.pow(-1, j) * prices[i]);
}
}
return dp[length - 1][2 * k];
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# C:
#define max(a, b) ((a) > (b) ? (a) : (b))
int maxProfit(int k, int* prices, int pricesSize) {
if(pricesSize == 0){
return 0;
}
int dp[pricesSize][2 * k + 1];
memset(dp, 0, sizeof(int) * pricesSize * (2 * k + 1));
for (int j = 1; j < 2 * k; j += 2) {
dp[0][j] = -prices[0];
}
for (int i = 1;i < pricesSize; i++) { // Iterate over stock
for (int j = 0; j < 2 * k - 1; j += 2) { // Update each buy and sell
dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);
dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
}
}
return dp[pricesSize - 1][2 * k];
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# Rust:
impl Solution {
pub fn max_profit(k: i32, prices: Vec<i32>) -> i32 {
let mut dp = vec![vec![0; 2 * k as usize + 1]; prices.len()];
for v in dp[0].iter_mut().skip(1).step_by(2) {
*v = -prices[0];
}
for (i, &p) in prices.iter().enumerate().skip(1) {
for j in (0..2 * k as usize - 1).step_by(2) {
dp[i][j + 1] = dp[i - 1][j + 1].max(dp[i - 1][j] - p);
dp[i][j + 2] = dp[i - 1][j + 2].max(dp[i - 1][j + 1] + p);
}
}
dp[prices.len() - 1][2 * k as usize]
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Space Optimization:
impl Solution {
pub fn max_profit(k: i32, prices: Vec<i32>) -> i32 {
let mut dp = vec![0; 2 * k as usize + 1];
for v in dp.iter_mut().skip(1).step_by(2) {
*v = -prices[0];
}
for p in prices {
for i in 1..=2 * k as usize {
if i % 2 == 1 {
// Buy
dp[i] = dp[i].max(dp[i - 1] - p);
continue;
}
// Sell
dp[i] = dp[i].max(dp[i - 1] + p);
}
}
dp[2 * k as usize]
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
