# 1049. Last Stone Weight II
LeetCode Problem Link (opens new window)
Difficulty: Medium
You have a collection of stones, each with a positive integer weight.
Each turn, we choose any two stones and smash them together. Suppose the stones have weights x and y with x <= y. The result of this smash is:
- If
x == y, both stones are totally destroyed; - If
x != y, the stone of weightxis totally destroyed, and the stone of weightyhas new weighty-x.
At the end, there is at most one stone left. Return the smallest possible weight of this stone. If there are no stones left, return 0.
Example:
- Input:
[2,7,4,1,8,1] - Output:
1
Explanation:
- Combine 2 and 4 to get 2, so the array turns into
[2,7,1,8,1], - Combine 7 and 8 to get 1, so the array turns into
[2,1,1,1], - Combine 2 and 1 to get 1, so the array turns into
[1,1,1], - Combine 1 and 1 to get 0, so the array turns into
[1], which is the optimal value.
Constraints:
1 <= stones.length <= 301 <= stones[i] <= 1000
# Thought Process
If you are not familiar with the knapsack problem, first refer to these two articles:
The problem is essentially about dividing the stones into two piles with as equal weight as possible, and the minimum remaining stone weight will be the difference between these two piles.
One pile has a weight of sum, so we try to make a pile with weight as close as possible to sum / 2. This transforms the problem into finding if we can fill a knapsack of capacity sum / 2 with the given stones.
At this point, the problem is very similar to 0416.Partition Equal Subset Sum-1 (opens new window).
This transforms the problem into a 01 Knapsack Problem.
In 0416.Partition Equal Subset Sum-1 (opens new window), we determine if the knapsack can be exactly filled, whereas in this problem, we determine the maximum weight that can be filled in the knapsack.
Each stone is an item, with weight stones[i] and value stones[i].
We will proceed with the dynamic programming five-step approach:
# 1. Define the dp array and its meaning
dp[j] indicates the maximum weight the knapsack can hold when its capacity is j.
In terms of the 01 Knapsack Problem, the item's weight is stones[i] and its value is also stones[i].
“Maximum value the knapsack can hold is dp[j]” is equivalent to “Maximum weight the knapsack can hold is dp[j].”
# 2. Determine the transfer equation
The transfer equation for the 01 Knapsack problem is: dp[j] = max(dp[j], dp[j - weight[i]] + value[i]).
For this problem, it is:
dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]).
# 3. Initialize the dp array
As capacities can't be negative, all dp[j] should be initialized to 0, ensuring that dp[j] will not be overwritten with initial values during recursion as in dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]).
vector<int> dp(15001, 0);
# 4. Determine the loop order
As explained in Knapsack Theory 01 Knapsack-2 (opens new window): When using a 1D dp array, loop over items in the outer loop, and loop over the knapsack's capacity in the inner loop, iterating backwards in the inner loop.
for (int i = 0; i < stones.size(); i++) { // Loop over items
for (int j = target; j >= stones[i]; j--) { // Loop over knapsack's capacity
dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
}
}
2
3
4
5
# 5. Illustrate dp array
Example, Input: [2,4,1,1], at target = (2 + 4 + 1 + 1)/2 = 4, the dp array states are:
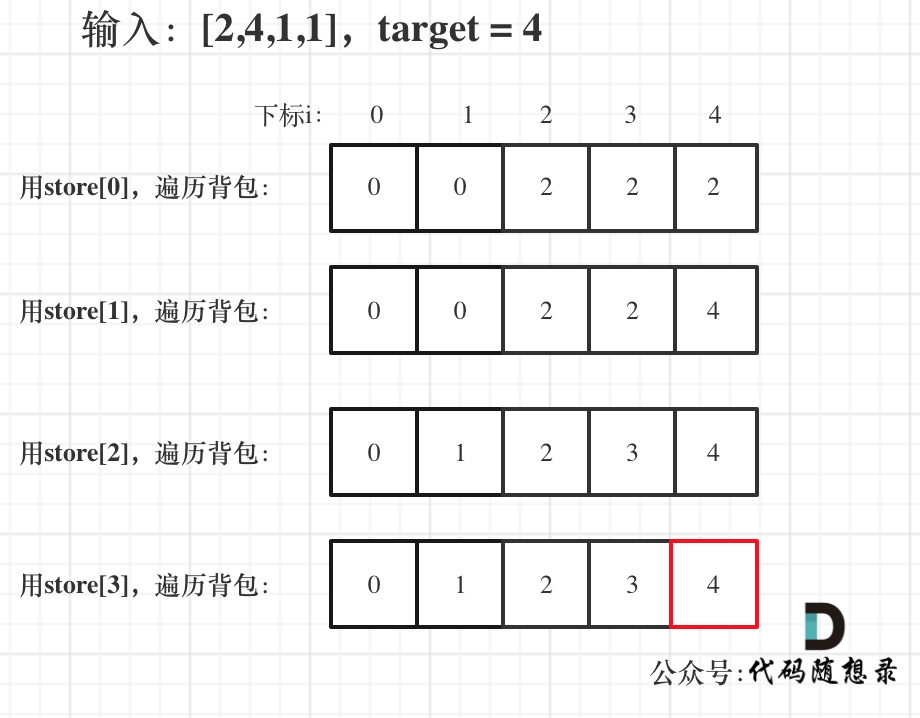
Finally, dp[target] shows the maximum weight the knapsack can carry for capacity target.
Stones are divided into two piles: one with total weight dp[target] and the other with sum - dp[target].
As target is sum / 2, and because sum / 2 is rounded down, sum - dp[target] is always greater than or equal to dp[target].
The minimal remaining stone weight is therefore (sum - dp[target]) - dp[target].
With this understanding, here's the C++ code:
class Solution {
public:
int lastStoneWeightII(vector<int>& stones) {
vector<int> dp(15001, 0);
int sum = 0;
for (int i = 0; i < stones.size(); i++) sum += stones[i];
int target = sum / 2;
for (int i = 0; i < stones.size(); i++) { // Loop over items
for (int j = target; j >= stones[i]; j--) { // Loop over knapsack's capacity
dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
}
}
return sum - dp[target] - dp[target];
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
- Time Complexity: O(m × n), where m is the total weight of stones (or half the total weight accurately), and n is the number of stones.
- Space Complexity: O(m)
# Summary
This problem is almost identical to 0416.Partition Equal Subset Sum-1 (opens new window), with the only difference being the final processing of dp[target].
While 0416.Partition Equal Subset Sum-1 (opens new window) seeks to determine if the knapsack can be exactly filled, this problem seeks the maximum weight that can be held by the knapsack.
# Other Language Versions
# Java:
1D array version:
class Solution {
public int lastStoneWeightII(int[] stones) {
int sum = 0;
for (int i : stones) {
sum += i;
}
int target = sum >> 1;
int[] dp = new int[target + 1];
for (int i = 0; i < stones.length; i++) {
for (int j = target; j >= stones[i]; j--) {
dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);
}
}
return sum - 2 * dp[target];
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2D array version (for understanding):
class Solution {
public int lastStoneWeightII(int[] stones) {
int sum = 0;
for (int s : stones) {
sum += s;
}
int target = sum / 2;
int[][] dp = new int[stones.length][target + 1];
for (int j = stones[0]; j <= target; j++) {
dp[0][j] = stones[0];
}
for (int i = 1; i < stones.length; i++) {
for (int j = 1; j <= target; j++) {
if (j >= stones[i]) {
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - stones[i]] + stones[i]);
} else {
dp[i][j] = dp[i - 1][j];
}
}
}
return (sum - dp[stones.length - 1][target]) - dp[stones.length - 1][target];
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# Python:
Cago version:
class Solution:
def lastStoneWeightII(self, stones: List[int]) -> int:
dp = [0] * 15001
total_sum = sum(stones)
target = total_sum // 2
for stone in stones:
for j in range(target, stone - 1, -1):
dp[j] = max(dp[j], dp[j - stone] + stone)
return total_sum - dp[target] - dp[target]
2
3
4
5
6
7
8
9
10
11
12
Simplified Cago version:
class Solution:
def lastStoneWeightII(self, stones):
total_sum = sum(stones)
target = total_sum // 2
dp = [0] * (target + 1)
for stone in stones:
for j in range(target, stone - 1, -1):
dp[j] = max(dp[j], dp[j - stone] + stone)
return total_sum - 2* dp[-1]
2
3
4
5
6
7
8
9
10
11
2D DP version:
class Solution:
def lastStoneWeightII(self, stones: List[int]) -> int:
total_sum = sum(stones)
target = total_sum // 2
dp = [[False] * (target + 1) for _ in range(len(stones) + 1)]
for i in range(len(stones) + 1):
dp[i][0] = True
for i in range(1, len(stones) + 1):
for j in range(1, target + 1):
if stones[i - 1] > j:
dp[i][j] = dp[i - 1][j]
else:
dp[i][j] = dp[i - 1][j] or dp[i - 1][j - stones[i - 1]]
for i in range(target, -1, -1):
if dp[len(stones)][i]:
return total_sum - 2 * i
return 0
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
1D DP version:
class Solution:
def lastStoneWeightII(self, stones):
total_sum = sum(stones)
target = total_sum // 2
dp = [False] * (target + 1)
dp[0] = True
for stone in stones:
for j in range(target, stone - 1, -1):
dp[j] = dp[j] or dp[j - stone]
for i in range(target, -1, -1):
if dp[i]:
return total_sum - 2 * i
return 0
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# Go:
1D dp
func lastStoneWeightII(stones []int) int {
dp := make([]int, 15001)
sum := 0
for _, v := range stones {
sum += v
}
target := sum / 2
for i := 0; i < len(stones); i++ {
for j := target; j >= stones[i]; j-- {
dp[j] = max(dp[j], dp[j-stones[i]]+stones[i])
}
}
return sum - 2 * dp[target]
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
2D dp
func lastStoneWeightII(stones []int) int {
sum := 0
for _, val := range stones {
sum += val
}
target := sum / 2
dp := make([][]int, len(stones))
for i := range dp {
dp[i] = make([]int, target + 1)
}
for j := stones[0]; j <= target; j++ {
dp[0][j] = stones[0]
}
for i := 1; i < len(stones); i++ {
for j := 0; j <= target; j++ {
if stones[i] > j {
dp[i][j] = dp[i-1][j]
} else {
dp[i][j] = max(dp[i-1][j], dp[i-1][j-stones[i]] + stones[i])
}
}
}
return (sum - dp[len(stones)-1][target]) - dp[len(stones)-1][target]
}
func max(x, y int) int {
if x > y {
return x
}
return y
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# JavaScript:
/**
* @param {number[]} stones
* @return {number}
*/
var lastStoneWeightII = function (stones) {
let sum = stones.reduce((s, n) => s + n);
let dpLen = Math.floor(sum / 2);
let dp = new Array(dpLen + 1).fill(0);
for (let i = 0; i < stones.length; ++i) {
for (let j = dpLen; j >= stones[i]; --j) {
dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);
}
}
return sum - dp[dpLen] - dp[dpLen];
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# C:
#define MAX(a, b) (((a) > (b)) ? (a) : (b))
int getSum(int *stones, int stoneSize) {
int sum = 0, i;
for (i = 0; i < stoneSize; ++i)
sum += stones[i];
return sum;
}
int lastStoneWeightII(int* stones, int stonesSize){
int sum = getSum(stones, stonesSize);
int target = sum / 2;
int i, j;
int *dp = (int*)malloc(sizeof(int) * (target + 1));
memset(dp, 0, sizeof(int) * (target + 1));
for (j = stones[0]; j <= target; ++j)
dp[j] = stones[0];
for (i = 1; i < stonesSize; ++i) {
for (j = target; j >= stones[i]; --j)
dp[j] = MAX(dp[j], dp[j - stones[i]] + stones[i]);
}
return sum - dp[target] - dp[target];
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# TypeScript:
function lastStoneWeightII(stones: number[]): number {
const sum: number = stones.reduce((a: number, b:number): number => a + b);
const target: number = Math.floor(sum / 2);
const n: number = stones.length;
const dp: number[] = new Array(target + 1).fill(0);
for (let i: number = 0; i < n; i++ ) {
for (let j: number = target; j >= stones[i]; j--) {
dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);
}
}
return sum - dp[target] - dp[target];
};
2
3
4
5
6
7
8
9
10
11
12
# Scala:
Rolling array:
object Solution {
def lastStoneWeightII(stones: Array[Int]): Int = {
var sum = stones.sum
var half = sum / 2
var dp = new Array[Int](half + 1)
for (i <- 0 until stones.length; j <- half to stones(i) by -1) {
dp(j) = math.max(dp(j), dp(j - stones(i)) + stones(i))
}
sum - 2 * dp(half)
}
}
2
3
4
5
6
7
8
9
10
11
12
13
2D array:
object Solution {
def lastStoneWeightII(stones: Array[Int]): Int = {
var sum = stones.sum
var half = sum / 2
var dp = Array.ofDim[Int](stones.length, half + 1)
for (j <- stones(0) to half) dp(0)(j) = stones(0)
for (i <- 1 until stones.length; j <- 1 to half) {
if (j - stones(i) >= 0) dp(i)(j) = stones(i) + dp(i - 1)(j - stones(i))
dp(i)(j) = math.max(dp(i)(j), dp(i - 1)(j))
}
sum - 2 * dp(stones.length - 1)(half)
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# Rust:
impl Solution {
pub fn last_stone_weight_ii(stones: Vec<i32>) -> i32 {
let sum = stones.iter().sum::<i32>();
let target = sum as usize / 2;
let mut dp = vec![0; target + 1];
for s in stones {
for j in (s as usize..=target).rev() {
dp[j] = dp[j].max(dp[j - s as usize] + s);
}
}
sum - dp[target] * 2
}
}
2
3
4
5
6
7
8
9
10
11
12
13
# C#
public class Solution
{
public int LastStoneWeightII(int[] stones)
{
int[] dp = new int[15001];
int sum = 0;
foreach (int stone in stones)
{
sum += stone;
}
int target = sum / 2;
for (int i = 0; i < stones.Length; i++)
{
for (int j = target; j >= stones[i]; j--)
{
dp[j] = Math.Max(dp[j], dp[j - stones[i]] + stones[i]);
}
}
return sum - 2 * dp[target];
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
