# 322. Coin Change
LeetCode Problem Link (opens new window)
Given different denominations of coins and a total amount of money amount. Write a function to compute the fewest number of coins that are needed to make up that amount. If that amount cannot be made up by any combination of the coins, return -1.
You may assume that you have an infinite number of each kind of coin.
Example 1:
- Input: coins = [1, 2, 5], amount = 11
- Output: 3
- Explanation: 11 = 5 + 5 + 1
Example 2:
- Input: coins = [2], amount = 3
- Output: -1
Example 3:
- Input: coins = [1], amount = 0
- Output: 0
Example 4:
- Input: coins = [1], amount = 1
- Output: 1
Example 5:
- Input: coins = [1], amount = 2
- Output: 2
Constraints:
- 1 <= coins.length <= 12
- 1 <= coins[i] <= 2^31 - 1
- 0 <= amount <= 10^4
# Approach
We have exchanged coins once in Dynamic Programming: 0518.Coin Change II (opens new window) and now we are exchanging them again, but with a different approach!
The problem states that the quantity of each coin is infinite, indicating a classic complete knapsack problem.
Dynamic Programming approach:
- Define the dp array and its meaning:
dp[j]: The minimum number of coins needed to make up the total amount j is dp[j]
- Determine the transition equation:
The minimum number of coins needed to make up the total amount j - coins[i] is dp[j - coins[i]], so just adding one coin coins[i] would make it dp[j - coins[i]] + 1 (considering coins[i]).
Thus, dp[j] should take the minimum from all dp[j - coins[i]] + 1.
Transition equation: dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
- Initialize the dp array:
First, the minimum number of coins needed to make up a total amount of 0 is definitely 0, thus dp[0] = 0;
What about other indices?
Considering the nature of the transition equation, the dp[j] must be initialized to a large value, otherwise, it will be overwritten by the initial value during the min comparison.
Thus, all non-zero indices should be initialized to the maximum value.
The code is as follows:
vector<int> dp(amount + 1, INT_MAX);
dp[0] = 0;
2
- Determine the order of traversal:
This problem asks for the minimum number of coins, so the sequence of coins matters or not does not affect the minimum number of coins.
So this problem does not emphasize whether the set is a combination or permutation.
If it's a combination, iterate over items with the outer loop, and over the knapsack with the inner loop.
If it's a permutation, iterate over the knapsack with the outer loop and over items with the inner loop.
In the dynamic programming topic, we talked about how to find combinations in Dynamic Programming: 0518.Coin Change II (opens new window), and how to find permutations in Dynamic Programming: 0377.Combination Sum IV (opens new window).
In this question, the two-for-loop relationship is: iterate over the items with the outer loop and the target with the inner loop, or iterate over the target with the outer loop and the items with the inner loop, both are feasible!
Therefore, I will use the coins in the outer loop, and the target in the inner loop.
Since the number of coins can be used infinitely, this is a complete knapsack problem, and the inner loop should proceed in the forward direction.
Thus, the order of traversal is: coins (items) are in the outer loop, target (knapsack) is in the inner loop, and the inner loop is in forward order.
- Derive the dp array using an example:
For input: coins = [1, 2, 5], amount = 5
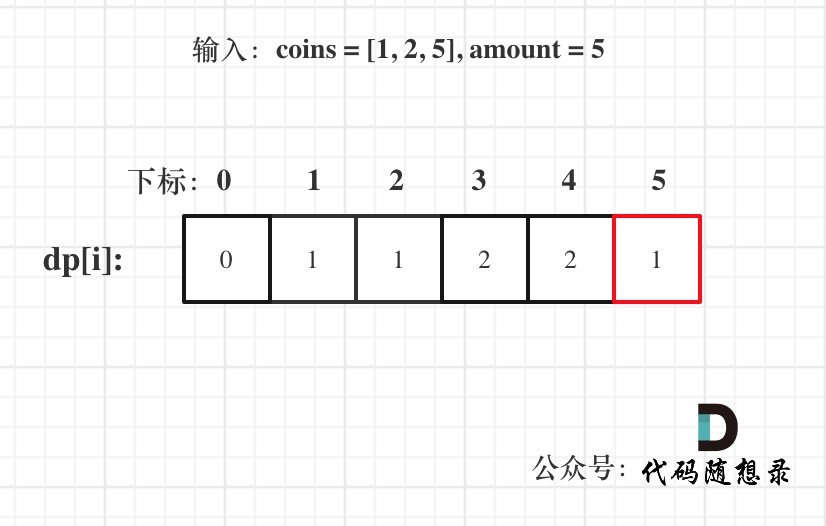
dp[amount] is the final result.
The above analysis is complete, and the C++ code is as follows:
// Version 1
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
vector<int> dp(amount + 1, INT_MAX);
dp[0] = 0;
for (int i = 0; i < coins.size(); i++) { // Iterate through items
for (int j = coins[i]; j <= amount; j++) { // Iterate through knapsack
if (dp[j - coins[i]] != INT_MAX) { // If dp[j - coins[i]] is the initial value, skip it
dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
}
}
}
if (dp[amount] == INT_MAX) return -1;
return dp[amount];
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
- Time complexity: O(n * amount), where n is the length of coins
- Space complexity: O(amount)
For the traversal method of putting the knapsack in the outer loop and the items in the inner loop is also feasible, I will directly provide the code.
// Version 2
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
vector<int> dp(amount + 1, INT_MAX);
dp[0] = 0;
for (int i = 1; i <= amount; i++) { // Iterate through the knapsack
for (int j = 0; j < coins.size(); j++) { // Iterate through items
if (i - coins[j] >= 0 && dp[i - coins[j]] != INT_MAX ) {
dp[i] = min(dp[i - coins[j]] + 1, dp[i]);
}
}
}
if (dp[amount] == INT_MAX) return -1;
return dp[amount];
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
- Same as above
# Summary
Attentive students who look at solutions online might find that one explanation puts the loop iterating over the knapsack on the outside and another puts it on the inside, and after seeing a lot, you might get confused about the order of these two loops.
There's barely an article that clarifies the order!
This is also the frustration faced by most students learning dynamic programming. Sometimes the transition equation is simple; the difficulty lies in the order of traversal!
But in the end, problems can be solved in a confusing way with no clear understanding of why they work; they just do.
This article clearly explains the traversal order for you.
In Dynamic Programming: 0518.Coin Change II (opens new window), we seek combinations, and in Dynamic Programming: 0377.Combination Sum IV (opens new window), we seek permutations.
And this problem asks for the minimum number of coins, whether they are combinations or permutations does not matter! So either order of the two for loops is acceptable!
That's why I talked about 518.Coin Change II before this problem, which is: 322.Coin Change, with good reason.
I believe after reading it, you have a better understanding of the traversal order in knapsack problems.
# Other Language Versions
# Java:
class Solution {
public int coinChange(int[] coins, int amount) {
int max = Integer.MAX_VALUE;
int[] dp = new int[amount + 1];
// Initialize dp array to maximum value
for (int j = 0; j < dp.length; j++) {
dp[j] = max;
}
// When the amount is 0, the number of coins needed is 0
dp[0] = 0;
for (int i = 0; i < coins.length; i++) {
// Forward traversal: Complete knapsack can select each coin multiple times
for (int j = coins[i]; j <= amount; j++) {
// Only when dp[j - coins[i]] is not the initial maximum value, this position needs to be chosen
if (dp[j - coins[i]] != max) {
// Choose the situation with the smallest number of coins
dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);
}
}
}
return dp[amount] == max ? -1 : dp[amount];
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# Python:
First, iterate over the items, then the knapsack
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
dp = [float('inf')] * (amount + 1) # Create a dynamic programming array, initialized to positive infinity
dp[0] = 0 # Initialize the minimum number of coins needed when the knapsack capacity is 0 to 0
for coin in coins: # Iterate over the coin list, equivalent to iterating over items
for i in range(coin, amount + 1): # Iterate over the knapsack capacity
if dp[i - coin] != float('inf'): # If dp[i - coin] is not the initial value, perform state transition
dp[i] = min(dp[i - coin] + 1, dp[i]) # Update the minimum number of coins
if dp[amount] == float('inf'): # If the final minimum number of coins for the knapsack capacity is still positive infinity, it indicates no solution
return -1
return dp[amount] # Return the minimum number of coins when the knapsack capacity is amount
2
3
4
5
6
7
8
9
10
11
12
13
First, iterate over the knapsack, then the items
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
dp = [float('inf')] * (amount + 1) # Create a dynamic programming array, initialized to positive infinity
dp[0] = 0 # Initialize the minimum number of coins needed when the knapsack capacity is 0 to 0
for i in range(1, amount + 1): # Iterate over the knapsack capacity
for j in range(len(coins)): # Iterate over the coin list, equivalent to iterating over items
if i - coins[j] >= 0 and dp[i - coins[j]] != float('inf'): # If dp[i - coins[j]] is not the initial value, perform state transition
dp[i] = min(dp[i - coins[j]] + 1, dp[i]) # Update the minimum number of coins
if dp[amount] == float('inf'): # If the final minimum number of coins for the knapsack capacity is still positive infinity, it indicates no solution
return -1
return dp[amount] # Return the minimum number of coins when the knapsack capacity is amount
2
3
4
5
6
7
8
9
10
11
12
13
First, iterate over the items, then the knapsack (optimized version)
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
dp = [float('inf')] * (amount + 1)
dp[0] = 0
for coin in coins:
for i in range(coin, amount + 1): # Perform optimization, start calculation from the knapsack that can fit, no need for comparison
# Update the minimum number of coins needed to make amount i
dp[i] = min(dp[i], dp[i - coin] + 1)
return dp[amount] if dp[amount] != float('inf') else -1
2
3
4
5
6
7
8
9
10
11
First, iterate over the knapsack, then the items (optimized version)
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
dp = [float('inf')] * (amount + 1)
dp[0] = 0
for i in range(1, amount + 1): # Iterate over the knapsack capacity
for coin in coins: # Iterate over items
if i >= coin:
# Update the minimum number of coins needed to make amount i
dp[i] = min(dp[i], dp[i - coin] + 1)
return dp[amount] if dp[amount] != float('inf') else -1
2
3
4
5
6
7
8
9
10
11
12
# Go:
// Version 1, First iterate over items, then the knapsack
func coinChange1(coins []int, amount int) int {
dp := make([]int, amount+1)
// Initialize dp[0]
dp[0] = 0
// Initialize to math.MaxInt32
for j := 1; j <= amount; j++ {
dp[j] = math.MaxInt32
}
// Iterate over items
for i := 0; i < len(coins); i++ {
// Iterate over knapsack
for j := coins[i]; j <= amount; j++ {
if dp[j-coins[i]] != math.MaxInt32 {
// Derivation formula
dp[j] = min(dp[j], dp[j-coins[i]]+1)
//fmt.Println(dp,j,i)
}
}
}
// If no solution found to fill the knapsack, return -1
if dp[amount] == math.MaxInt32 {
return -1
}
return dp[amount]
}
// Version 2, First iterate over the knapsack, then the items
func coinChange2(coins []int, amount int) int {
dp := make([]int, amount+1)
// Initialize dp[0]
dp[0] = 0
// Iterate over knapsack starting from 1
for j := 1; j <= amount; j++ {
// Initialize to math.MaxInt32
dp[j] = math.MaxInt32
// Iterate over items
for i := 0; i < len(coins); i++ {
if j >= coins[i] && dp[j-coins[i]] != math.MaxInt32 {
// Derivation formula
dp[j] = min(dp[j], dp[j-coins[i]]+1)
//fmt.Println(dp)
}
}
}
// If no solution found to fill the knapsack, return -1
if dp[amount] == math.MaxInt32 {
return -1
}
return dp[amount]
}
func min(a, b int) int {
if a < b {
return a
}
return b
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
# C
#define min(a, b) ((a) > (b) ? (b) : (a))
int coinChange(int* coins, int coinsSize, int amount) {
int* dp = (int*)malloc(sizeof(int) * (amount + 1));
for (int j = 0; j < amount + 1; j++) {
dp[j] = INT_MAX;
}
dp[0] = 0;
// Iterate over knapsack
for(int i = 0; i <= amount; i++){
// Iterate over items
for(int j = 0; j < coinsSize; j++){
if(i - coins[j] >= 0 && dp[i - coins[j]] != INT_MAX){
dp[i] = min(dp[i], dp[i - coins[j]] + 1);
}
}
}
if(dp[amount] == INT_MAX){
return -1;
}
return dp[amount];
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# Rust:
// Iterate over items
impl Solution {
pub fn coin_change(coins: Vec<i32>, amount: i32) -> i32 {
let amount = amount as usize;
let mut dp = vec![i32::MAX; amount + 1];
dp[0] = 0;
for coin in coins {
for i in coin as usize..=amount {
if dp[i - coin as usize] != i32::MAX {
dp[i] = dp[i].min(dp[i - coin as usize] + 1);
}
}
}
if dp[amount] == i32::MAX {
return -1;
}
dp[amount]
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// Iterate over the knapsack
impl Solution {
pub fn coin_change(coins: Vec<i32>, amount: i32) -> i32 {
let amount = amount as usize;
let mut dp = vec![i32::MAX; amount + 1];
dp[0] = 0;
for i in 1..=amount {
for &coin in &coins {
if i >= coin as usize && dp[i - coin as usize] != i32::MAX {
dp[i] = dp[i].min(dp[i - coin as usize] + 1)
}
}
}
if dp[amount] == i32::MAX {
return -1;
}
dp[amount]
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# JavaScript:
// Iterate over items
const coinChange = (coins, amount) => {
if(!amount) {
return 0;
}
let dp = Array(amount + 1).fill(Infinity);
dp[0] = 0;
for(let i = 0; i < coins.length; i++) {
for(let j = coins[i]; j <= amount; j++) {
dp[j] = Math.min(dp[j - coins[i]] + 1, dp[j]);
}
}
return dp[amount] === Infinity ? -1 : dp[amount];
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// Iterate over the knapsack
var coinChange = function(coins, amount) {
const dp = Array(amount + 1).fill(Infinity)
dp[0] = 0
for (let i = 1; i <= amount; i++) {
for (let j = 0; j < coins.length; j++) {
if (i >= coins[j] && dp[i - coins[j]] !== Infinity) {
dp[i] = Math.min(dp[i], dp[i - coins[j]] + 1)
}
}
}
return dp[amount] === Infinity ? -1 : dp[amount]
}
2
3
4
5
6
7
8
9
10
11
12
13
# TypeScript:
// Iterate over items
function coinChange(coins: number[], amount: number): number {
const dp: number[] = new Array(amount + 1).fill(Infinity);
dp[0] = 0;
for (let i = 0; i < coins.length; i++) {
for (let j = coins[i]; j <= amount; j++) {
if (dp[j - coins[i]] === Infinity) continue;
dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);
}
}
return dp[amount] === Infinity ? -1 : dp[amount];
};
2
3
4
5
6
7
8
9
10
11
12
// Iterate over the knapsack
function coinChange(coins: number[], amount: number): number {
const dp: number[] = Array(amount + 1).fill(Infinity)
dp[0] = 0
for (let i = 1; i <= amount; i++) {
for (let j = 0; j < coins.length; j++) {
if (i >= coins[j] && dp[i - coins[j]] !== Infinity) {
dp[i] = Math.min(dp[i], dp[i - coins[j]] + 1)
}
}
}
return dp[amount] === Infinity ? -1 : dp[amount]
}
2
3
4
5
6
7
8
9
10
11
12
13
