300. Longest Increasing Subsequence

LeetCode Problem Link (opens new window)

Given an integer array nums, find the length of the longest strictly increasing subsequence.

A subsequence is a sequence derived from an array by deleting some or no elements without changing the order of the remaining elements. For example, [3,6,2,7] is a subsequence of the array [0,3,1,6,2,2,7].

Example 1:

• Input: nums = [10,9,2,5,3,7,101,18]
• Output: 4
• Explanation: The longest increasing subsequence is [2,3,7,101], therefore the length is 4.

Example 2:

• Input: nums = [0,1,0,3,2,3]
• Output: 4

Example 3:

• Input: nums = [7,7,7,7,7,7,7]
• Output: 1

Constraints:

• 1 <= nums.length <= 2500
• -10^4 <= nums[i] <= 10^4

Approach

First, through this problem, you need to clarify what a subsequence is: "A subsequence is a sequence derived from an array by deleting some or no elements without changing the order of the remaining elements."

This problem is the introductory problem for subsequence problems in dynamic programming. If you haven't encountered such problems before, it can be very challenging. You might not even know how to start a brute force search. Subsequence problems are classic problems solved using dynamic programming. The length of the strictly increasing subsequence ending at the current index i is related to the subsequence length of the previous index j. But what is this relationship?

Next, let's use the five steps of dynamic programming to analyze this problem in detail:

1. Definition of dp[i]

In this problem, correctly defining the significance of the dp array is very important.

dp[i] represents the length of the longest increasing subsequence ending with nums[i] up to and including i.

Why must it represent the "longest increasing subsequence ending with nums[i]"? Because when we make the increasing comparison of nums[j] and nums[i], the two increasing subsequences must end with nums[j] and nums[i] respectively, otherwise, how would the comparison make sense if they are not the tail elements?

2. State Transition Equation

The longest increasing subsequence ending at position i is equal to the length of the longest increasing subsequences at positions j from 0 to i-1 + 1.

Thus: if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);

Note that here we are not comparing dp[i] with dp[j] + 1, but we want to take the maximum value of dp[j] + 1.

3. Initialization of dp[i]

The initial size of the longest increasing subsequence for each i, corresponding to dp[i], is at least 1.

4. Determine Traversal Order

dp[i] is derived from the longest increasing subsequence of each position j from 0 to i-1, so the iteration of i must traverse from front to back.

j actually traverses from 0 to i-1, and it doesn't matter whether it goes from front to back or back to front, as long as all the elements from 0 to i-1 are traversed. By default, we traverse from front to back.

The outer loop iterates over i, and the inner loop iterates over j, as shown in the code below:

for (int i = 1; i < nums.size(); i++) {
    for (int j = 0; j < i; j++) {
        if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
    }
    if (dp[i] > result) result = dp[i]; // Pick the longer subsequence
}

5. Example to Derive the dp Array

Input: [0,1,0,3,2], the changes of the dp array are as follows:

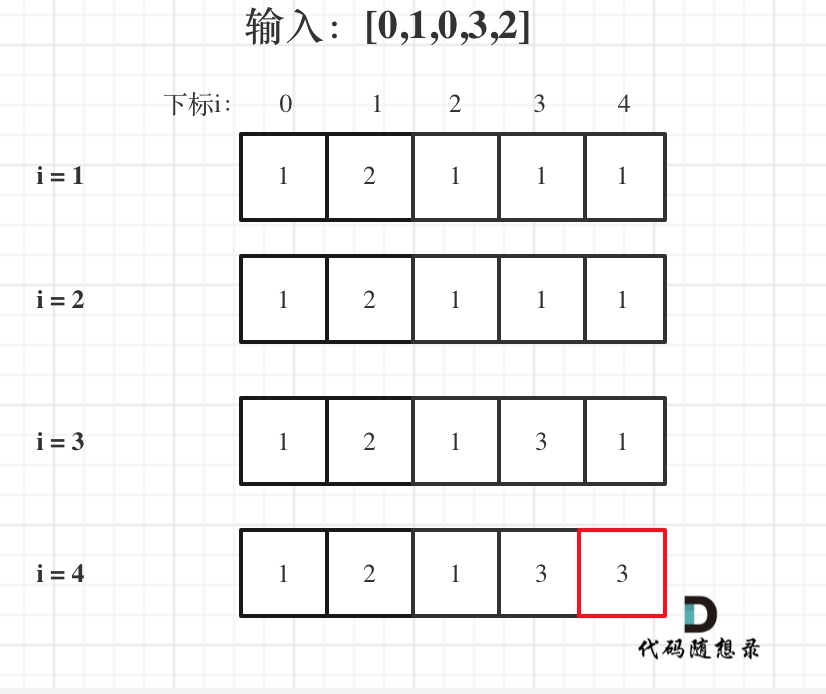
If your code compiles but doesn't pass the test cases, print out the dp array to verify its correctness!

Having completed the above five steps of analysis, the C++ code is provided below:

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        if (nums.size() <= 1) return nums.size();
        vector<int> dp(nums.size(), 1);
        int result = 0;
        for (int i = 1; i < nums.size(); i++) {
            for (int j = 0; j < i; j++) {
                if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
            }
            if (dp[i] > result) result = dp[i]; // Pick the longer subsequence
        }
        return result;
    }
};

• Time Complexity: O(n^2)
• Space Complexity: O(n)

Summary

The key to this problem is thinking about which states dp[i] can be derived from and taking the maximum value. Naturally, this leads to the recurrence relation: dp[i] = max(dp[i], dp[j] + 1);.

Subsequence problems are an important series in dynamic programming, and this problem serves as an introductory problem with more challenges to follow!

Versions in Other Languages

Java:

class Solution {
    public int lengthOfLIS(int[] nums) {
        if (nums.length <= 1) return nums.length;
        int[] dp = new int[nums.length];
        int res = 1;
        Arrays.fill(dp, 1);
        for (int i = 1; i < dp.length; i++) {
            for (int j = 0; j < i; j++) {
                if (nums[i] > nums[j]) {
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
            }
            res = Math.max(res, dp[i]);
        }
        return res;
    }
}

Python:

DP

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        if len(nums) <= 1:
            return len(nums)
        dp = [1] * len(nums)
        result = 1
        for i in range(1, len(nums)):
            for j in range(0, i):
                if nums[i] > nums[j]:
                    dp[i] = max(dp[i], dp[j] + 1)
            result = max(result, dp[i]) # Pick the longer subsequence
        return result

Greedy

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        if len(nums) <= 1:
            return len(nums)
        
        tails = [nums[0]]  # Store the tail elements of the increasing subsequence
        for num in nums[1:]:
            if num > tails[-1]:
                tails.append(num)  # If the current element is greater than the last element of the increasing subsequence, append it to the end
            else:
                # Use binary search to find the position of the current element in the increasing subsequence and replace the corresponding element
                left, right = 0, len(tails) - 1
                while left < right:
                    mid = (left + right) // 2
                    if tails[mid] < num:
                        left = mid + 1
                    else:
                        right = mid
                tails[left] = num
        
        return len(tails)  # Return the length of the increasing subsequence

Go:

// Dynamic programming solution
func lengthOfLIS(nums []int) int {
    // Definition of dp array: dp[i] represents the length of the subsequence including the i-th element ending with nums[i]
    dp := make([]int, len(nums))

    // Initialization: all elements should be initialized to 1
    for i := range dp {
        dp[i] = 1
    }

    ans := dp[0]
    for i := 1; i < len(nums); i++ {
        for j := 0; j < i; j++ {
            if nums[i] > nums[j] {
                dp[i] = max(dp[i], dp[j] + 1)
            }
        }
        if dp[i] > ans {
            ans = dp[i]
        }
    }
    return ans
}

func max(x, y int) int {
    if x > y {
        return x
    }
    return y
}

Greedy + Binary Optimization

func lengthOfLIS(nums []int ) int {
  dp := []int{}
  for _, num := range nums {
      if len(dp) == 0 || dp[len(dp) - 1] < num {
      dp = append(dp, num)
    } else {
          l, r := 0, len(dp) - 1
          pos := r
          for l <= r {
              mid := (l + r) >> 1
              if dp[mid] >= num {
                  pos = mid;
                  r = mid - 1
              } else {
                  l = mid + 1
              }
          }
          dp[pos] = num
      }// Binary search
  }
    return len(dp)
}

JavaScript:

const lengthOfLIS = (nums) => {
    let dp = Array(nums.length).fill(1);
    let result = 1;

    for(let i = 1; i < nums.length; i++) {
        for(let j = 0; j < i; j++) {
            if(nums[i] > nums[j]) {
                dp[i] = Math.max(dp[i], dp[j]+1);
            }
        }
        result = Math.max(result, dp[i]);
    }

    return result;
};

TypeScript:

function lengthOfLIS(nums: number[]): number {
    /**
        dp[i]: The length of the longest subsequence including the i-th element ending with nums[i]
     */
    const dp: number[] = new Array(nums.length).fill(1);
    let resMax: number = 0;
    for (let i = 0, length = nums.length; i < length; i++) {
        for (let j = 0; j < i; j++) {
            if (nums[i] > nums[j]) {
                dp[i] = Math.max(dp[i], dp[j] + 1);
            }
        }
        resMax = Math.max(resMax, dp[i]);
    }
    return resMax;
};

C:

#define max(a, b) ((a) > (b) ? (a) : (b))

int lengthOfLIS(int* nums, int numsSize) {
    if(numsSize <= 1){
        return numsSize;
    }
    int dp[numsSize];
    for(int i = 0; i < numsSize; i++){
        dp[i]=1;
    }
    int result = 1;
    for (int i = 1; i < numsSize; ++i) {
        for (int j = 0; j < i; ++j) {
            if(nums[i] > nums[j]){
                dp[i] = max(dp[i], dp[j] + 1);
            }
            if(dp[i] > result){
                result = dp[i];
            }
        }
    }
    return result;
}

Rust:

pub fn length_of_lis(nums: Vec<i32>) -> i32 {
    let mut dp = vec![1; nums.len()];
    let mut result = 1;
    for i in 1..nums.len() {
        for j in 0..i {
            if nums[j] < nums[i] {
                dp[i] = dp[i].max(dp[j] + 1);
            }
            result = result.max(dp[i]);
        }
    }
    result
}

Cangjie:

func lengthOfLIS(nums: Array<Int64>): Int64 {
    let n = nums.size
    if (n <= 1) {
        return n
    }

    let dp = Array(n, item: 1)
    var res = 0
    for (i in 1..n) {
        for (j in 0..i) {
            if (nums[i] > nums[j]) {
                dp[i] = max(dp[i], dp[j] + 1)
            }
        }
        res = max(dp[i], res)
    }
    return res
}