# 674. Longest Continuous Increasing Subsequence
LeetCode Problem Link (opens new window)
Given an unsorted array of integers, find the length of the longest continuous increasing subsequence (subarray).
A continuous increasing subsequence can be represented by two indices l and r (l < r) such that for every l <= i < r, nums[i] < nums[i + 1]. The subsequence [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] is a continuous increasing subsequence.
Example 1:
- Input: nums = [1,3,5,4,7]
- Output: 3
- Explanation: The longest continuous increasing subsequence is [1,3,5], with a length of 3. Although [1,3,5,7] is an increasing subsequence, it's not continuous because 5 and 7 are separated by 4 in the original array.
Example 2:
- Input: nums = [2,2,2,2,2]
- Output: 1
- Explanation: The longest continuous increasing subsequence is [2], with a length of 1.
Constraints:
- 0 <= nums.length <= 10^4
- -10^9 <= nums[i] <= 10^9
# Approach
The biggest difference between this problem and yesterday's 0300.Longest Increasing Subsequence (opens new window) is "continuity."
This problem requires the longest continuous increasing subsequence.
# Dynamic Programming
Let's analyze dynamic programming in five steps:
- Define the
dparray (dp table) and the meaning of its indices.
dp[i]: The length of the continuous increasing subsequence that ends with index i.
Notice that the definition is for subsequences ending with index i, not necessarily starting from index 0.
- Define the recurrence relation.
If nums[i] > nums[i - 1], then the length of the continuous increasing subsequence ending at i must equal the length of the continuous increasing subsequence ending at i - 1 plus 1.
That is: dp[i] = dp[i - 1] + 1;
Notice the difference with 0300.Longest Increasing Subsequence (opens new window)!
Because this problem requires a continuous increasing subsequence, we only need to compare nums[i] with nums[i - 1], and not compare all nums[j] with nums[i] where j is in the range from 0 to i.
Since we don't need j, a single loop is sufficient for this problem, only comparing nums[i] and nums[i - 1].
You should really grasp this point!
- Initialize the
dparray.
The length of a continuous increasing subsequence that ends at index i must be at least 1, i.e., just the element nums[i].
So dp[i] should be initialized to 1;
- Determine the order of traversal.
From the recurrence relation, dp[i + 1] depends on dp[i], so we must traverse from the beginning to the end.
In the construction of the recurrence relation, we also explained why a single loop is sufficient for this problem. Here's the code:
for (int i = 1; i < nums.size(); i++) {
if (nums[i] > nums[i - 1]) { // Record continuously
dp[i] = dp[i - 1] + 1;
}
}
2
3
4
5
- Walkthrough an example of the
dparray.
Using input nums = [1,3,5,4,7] as an example, the state of the dp array would be:
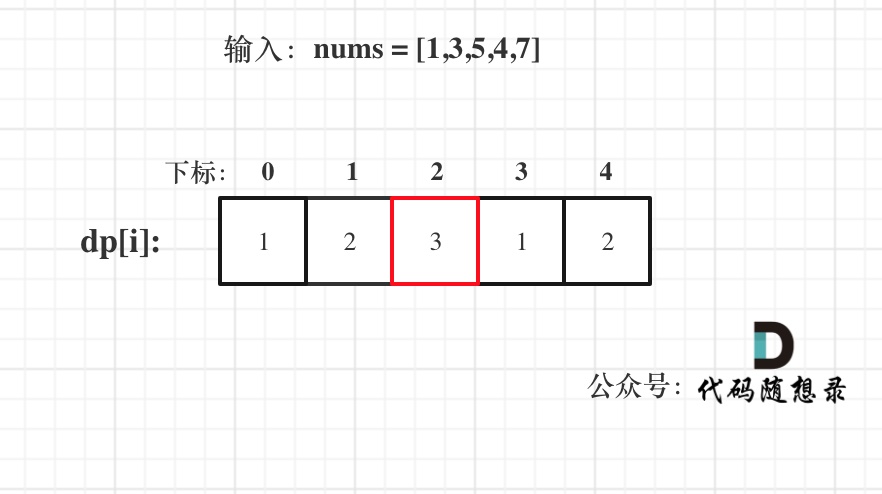
Remember to take the maximum value from the dp[i] array, so dp[2] is the result!
The above analysis is complete, and the C++ code is as follows:
class Solution {
public:
int findLengthOfLCIS(vector<int>& nums) {
if (nums.size() == 0) return 0;
int result = 1;
vector<int> dp(nums.size() ,1);
for (int i = 1; i < nums.size(); i++) {
if (nums[i] > nums[i - 1]) { // Record continuously
dp[i] = dp[i - 1] + 1;
}
if (dp[i] > result) result = dp[i];
}
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
- Time Complexity: O(n)
- Space Complexity: O(n)
# Greedy
This problem can also be solved using a greedy approach, which simply increments the count whenever nums[i] > nums[i - 1], resetting the count to 1 otherwise while keeping track of the maximum count.
The code is below:
class Solution {
public:
int findLengthOfLCIS(vector<int>& nums) {
if (nums.size() == 0) return 0;
int result = 1; // The minimum length of the continuous subsequence is 1
int count = 1;
for (int i = 1; i < nums.size(); i++) {
if (nums[i] > nums[i - 1]) { // Record continuously
count++;
} else { // Not continuous, reset count
count = 1;
}
if (count > result) result = count;
}
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
- Time Complexity: O(n)
- Space Complexity: O(1)
# Conclusion
This is also a classic problem of subsequences in dynamic programming, but it can also be solved using a greedy approach, which seems simpler and has a space complexity of only O(1).
In the dynamic programming analysis, the key is to understand the difference between this and 0300.Longest Increasing Subsequence (opens new window).
Link them together to understand how to find an increasing subsequence and then how to find a continuous increasing subsequence.
In summary: the non-continuous increasing subsequence is related to previous states from 0 to i, while the continuous one is only related to the previous state.
I've highlighted the differences in the recurrence relation and traversal method, so please take your time to grasp them!
# Other Language Versions
# Java:
Dynamic Programming:
/**
* 1.dp[i] represents the maximum continuous value at current index
* 2.Recurrence relation: if(nums[i+1] > nums[i]) then dp[i+1] = dp[i]+1
* 3.Initialization: All values set to 1
* 4.Traversal direction: Front to back
* 5.Result derivation:
* @param nums
* @return
*/
public static int findLengthOfLCIS(int[] nums) {
int[] dp = new int[nums.length];
for (int i = 0; i < dp.length; i++) {
dp[i] = 1;
}
int res = 1;
// Note that here, i starts from 0, which causes some differences compared to Carl's C++ code, where some places have an offset of i + 1.
for (int i = 0; i < nums.length - 1; i++) {
if (nums[i + 1] > nums[i]) {
dp[i + 1] = dp[i] + 1;
}
res = res > dp[i + 1] ? res : dp[i + 1];
}
return res;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
Dynamic Programming with State Compression
class Solution {
public int findLengthOfLCIS(int[] nums) {
// Record the length of the longest continuous increasing subsequence ending at the previous element
// and at the current element.
int beforeOneMaxLen = 1, currentMaxLen = 0;
// Initialize `res` to the minimum value, returning at least 1
int res = 1;
for (int i = 1; i < nums.length; i++) {
currentMaxLen = nums[i] > nums[i - 1] ? beforeOneMaxLen + 1 : 1;
beforeOneMaxLen = currentMaxLen;
res = Math.max(res, currentMaxLen);
}
return res;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Greedy Approach:
public static int findLengthOfLCIS(int[] nums) {
if (nums.length == 0) return 0;
int res = 1; // Minimum length is 1
int count = 1;
for (int i = 0; i < nums.length - 1; i++) {
if (nums[i + 1] > nums[i]) { // Record continuously
count++;
} else { // Not continuous, reset count
count = 1;
}
if (count > res) res = count;
}
return res;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
# Python:
Dynamic Programming
class Solution:
def findLengthOfLCIS(self, nums: List[int]) -> int:
if len(nums) == 0:
return 0
result = 1
dp = [1] * len(nums)
for i in range(len(nums)-1):
if nums[i+1] > nums[i]: # Record continuously
dp[i+1] = dp[i] + 1
result = max(result, dp[i+1])
return result
2
3
4
5
6
7
8
9
10
11
Dynamic Programming (Optimized Version)
class Solution:
def findLengthOfLCIS(self, nums: List[int]) -> int:
if not nums:
return 0
max_length = 1
current_length = 1
for i in range(1, len(nums)):
if nums[i] > nums[i - 1]:
current_length += 1
max_length = max(max_length, current_length)
else:
current_length = 1
return max_length
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Greedy
class Solution:
def findLengthOfLCIS(self, nums: List[int]) -> int:
if len(nums) == 0:
return 0
result = 1 # The minimum length is 1
count = 1
for i in range(len(nums)-1):
if nums[i+1] > nums[i]: # Record continuously
count += 1
else: # Not continuous, reset count
count = 1
result = max(result, count)
return result
2
3
4
5
6
7
8
9
10
11
12
13
# Go:
Dynamic Programming:
func findLengthOfLCIS(nums []int) int {
if len(nums) == 0 {return 0}
res, count := 1, 1
for i := 0; i < len(nums)-1; i++ {
if nums[i+1] > nums[i] {
count++
}else {
count = 1
}
if count > res {
res = count
}
}
return res
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Greedy Algorithm:
func findLengthOfLCIS(nums []int) int {
if len(nums) == 0 {return 0}
dp := make([]int, len(nums))
for i := 0; i < len(dp); i++ {
dp[i] = 1
}
res := 1
for i := 0; i < len(nums)-1; i++ {
if nums[i+1] > nums[i] {
dp[i+1] = dp[i] + 1
}
if dp[i+1] > res {
res = dp[i+1]
}
}
return res
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# Rust:
Dynamic Programming
pub fn find_length_of_lcis(nums: Vec<i32>) -> i32 {
if nums.is_empty() {
return 0;
}
let mut result = 1;
let mut dp = vec![1; nums.len()];
for i in 1..nums.len() {
if nums[i - 1] < nums[i] {
dp[i] = dp[i - 1] + 1;
result = result.max(dp[i]);
}
}
result
}
2
3
4
5
6
7
8
9
10
11
12
13
14
Greedy
impl Solution {
pub fn find_length_of_lcis(nums: Vec<i32>) -> i32 {
let (mut res, mut count) = (1, 1);
for i in 1..nums.len() {
if nums[i] > nums[i - 1] {
count += 1;
res = res.max(count);
continue;
}
count = 1;
}
res
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
# JavaScript:
Dynamic Programming:
const findLengthOfLCIS = (nums) => {
let dp = new Array(nums.length).fill(1);
for(let i = 0; i < nums.length - 1; i++) {
if(nums[i+1] > nums[i]) {
dp[i+1] = dp[i]+ 1;
}
}
return Math.max(...dp);
};
2
3
4
5
6
7
8
9
10
11
Greedy Approach:
const findLengthOfLCIS = (nums) => {
if(nums.length === 1) {
return 1;
}
let maxLen = 1;
let curMax = 1;
let cur = nums[0];
for(let num of nums) {
if(num > cur) {
curMax += 1;
maxLen = Math.max(maxLen, curMax);
} else {
curMax = 1;
}
cur = num;
}
return maxLen;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# TypeScript:
Dynamic Programming:
function findLengthOfLCIS(nums: number[]): number {
/**
dp[i]: The longest continuous subarray length ending at nums[i]
*/
const dp: number[] = new Array(nums.length).fill(1);
let resMax: number = 1;
for (let i = 1, length = nums.length; i < length; i++) {
if (nums[i] > nums[i - 1]) {
dp[i] = dp[i - 1] + 1;
}
resMax = Math.max(resMax, dp[i]);
}
return resMax;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
Greedy:
function findLengthOfLCIS(nums: number[]): number {
let resMax: number = 1;
let count: number = 1;
for (let i = 0, length = nums.length; i < length - 1; i++) {
if (nums[i] < nums[i + 1]) {
count++;
} else {
count = 1;
}
resMax = Math.max(resMax, count);
}
return resMax;
};
2
3
4
5
6
7
8
9
10
11
12
13
# C:
Dynamic Programming:
int findLengthOfLCIS(int* nums, int numsSize) {
if(numsSize == 0){
return 0;
}
int dp[numsSize];
for(int i = 0; i < numsSize; i++){
dp[i] = 1;
}
int result = 1;
for (int i = 1; i < numsSize; ++i) {
if(nums[i] > nums[i - 1]){
dp[i] = dp[i - 1] + 1;
}
if(dp[i] > result){
result = dp[i];
}
}
return result;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Greedy:
int findLengthOfLCIS(int* nums, int numsSize) {
int result = 1;
int count = 1;
if(numsSize == 0){
return result;
}
for (int i = 1; i < numsSize; ++i) {
if(nums[i] > nums[i - 1]){
count++;
} else{
count = 1;
}
if(count > result){
result = count;
}
}
return result;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# Cangjie
func findLengthOfLCIS(nums: Array<Int64>): Int64 {
let n = nums.size
if (n <= 1) {
return n
}
let dp = Array(n, repeat: 1)
var res = 0
for (i in 1..n) {
if (nums[i] > nums[i - 1]) {
dp[i] = dp[i - 1] + 1
}
res = max(res, dp[i])
}
return res
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
