96. Unique Binary Search Trees

LeetCode Problem Link (opens new window)

Given an integer n, find how many structurally unique BST's (binary search trees) that store values 1 ... n.

Example:

Approach

This problem statement is quite brief, and many students might feel confused about how to approach it.

If you need a refresher on what a binary search tree is, you might want to review the article 0700.Search in a Binary Search Tree (opens new window).

After understanding binary search trees, let's try a few examples and draw some diagrams to see if any patterns emerge, as shown below:

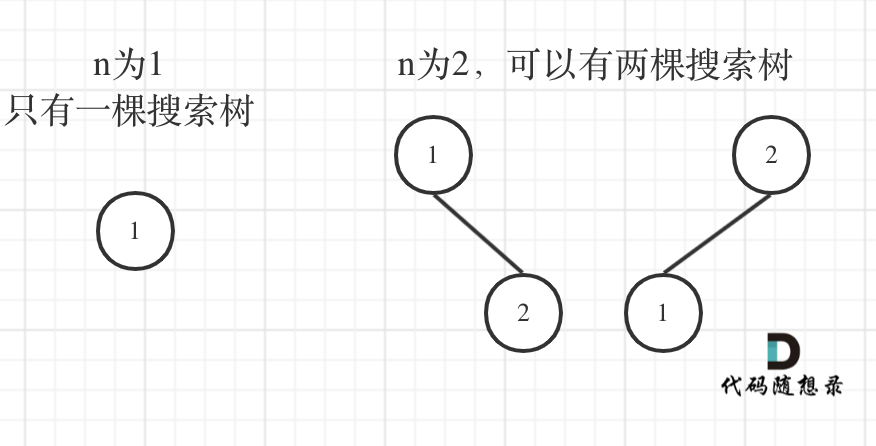
When n is 1, there is one tree, and when n is 2, there are two trees, which is quite intuitive.

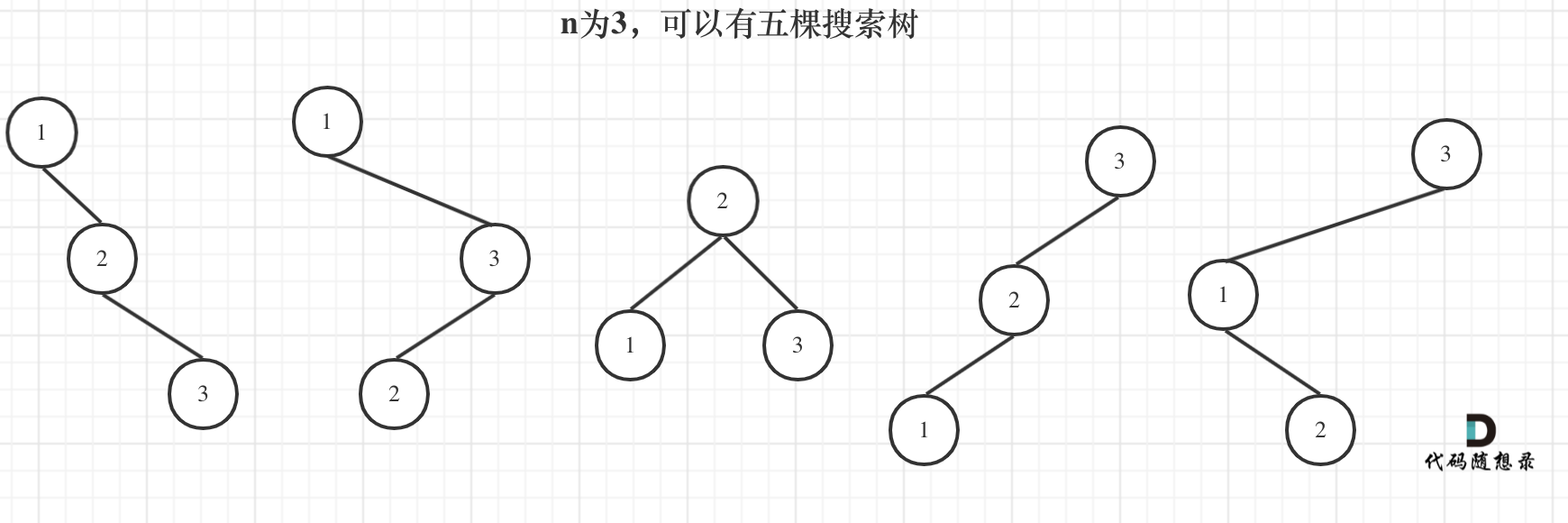
Let's see the cases when n is 3.

When 1 is the root node, its right subtree has two nodes. The layout of these two nodes is similar to the two trees when n is 2!

(Some might question the difference in layout due to different values. Remember, we only need to count the number of unique trees, so we don't care about the specific values or differences.)

When 3 is the root node, its left subtree has two nodes, which also resembles the layout when n is 2!

When 2 is the root node, its left and right subtrees both only have one node, resembling the tree layout when n is 1!

Here, we've found the overlapping sub-problems. You can derive dp[3] using dp[1] and dp[2].

dp[3] is the number of BSTs with element 1 as the root + element 2 as the root + element 3 as the root.

• The number of BSTs with element 1 as the root is equal to the number of BSTs with 2 nodes in the right subtree * the number of BSTs with 0 nodes in the left subtree.
• The number of BSTs with element 2 as the root is equal to the number of BSTs with 1 node in the right subtree * the number of BSTs with 1 node in the left subtree.
• The number of BSTs with element 3 as the root is equal to the number of BSTs with 0 nodes in the right subtree * the number of BSTs with 2 nodes in the left subtree.

The number of trees with 2 nodes is dp[2].

The number of trees with 1 node is dp[1].

The number of trees with 0 nodes is dp[0].

So, dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2].

Illustrated in the diagram:

Now that we have found the recursive relation, let's analyze this problem systematically using the dynamic programming five-step approach.

1. Define the dp array (dp table) and the meaning of its indices.

   dp[i]: The number of unique BSTs that can be formed with i nodes numbered from 1 to i.

2. Determine the recursive formula.

   In our analysis, we found the recurrence relation: dp[i] += dp[j - 1] * dp[i - j]; where j varies from 1 to i and represents the root element.

3. Initialize the dp array.

   Initialization only requires dp[0], which is the base condition for all calculations.

   Theoretically, an empty node is also a binary search tree. Thus, setting dp[0] = 1 makes sense.

4. Decide the traversal order.

   We start with the number of nodes, and the state with i nodes depends on previous states with fewer nodes.

   The loop for each number of nodes:

   for (int i = 1; i <= n; i++) {
       for (int j = 1; j <= i; j++) {
           dp[i] += dp[j - 1] * dp[i - j];
       }
   }
   

5. Example walkthrough of the dp array.

   The state of the dp array when n is 5 is illustrated below:

   

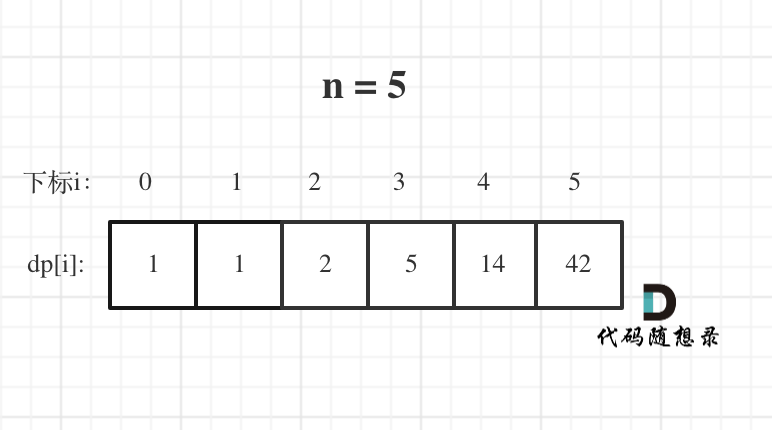
   Usually, you only need examples up to n = 3. Examples beyond that can be quite complex.

The C++ code is as follows:

class Solution {
public:
    int numTrees(int n) {
        vector<int> dp(n + 1);
        dp[0] = 1;
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= i; j++) {
                dp[i] += dp[j - 1] * dp[i - j];
            }
        }
        return dp[n];
    }
};

• Time Complexity: $O(n^2)$
• Space Complexity: $O(n)$

You may notice that after such extensive analysis, the code remains simple!

Conclusion

Although this is marked as medium difficulty, it can be challenging!

First, realizing that this problem can be solved using dynamic programming isn't very intuitive. You need to use examples and diagrams to find the recursive relation.

Once you determine the recursion, setting the initial conditions and traversal order is straightforward.

The dynamic programming five-step approach covers every aspect of the problem effectively!

Code in Other Languages

Java

class Solution {
    public int numTrees(int n) {
        // Initialize the dp array
        int[] dp = new int[n + 1];
        // Initialize the scenarios for 0 and 1 node
        dp[0] = 1;
        dp[1] = 1;
        for (int i = 2; i <= n; i++) {
            for (int j = 1; j <= i; j++) {
                // For each i, aggregate cases with j as the root
                dp[i] += dp[j - 1] * dp[i - j];
            }
        }
        return dp[n];
    }
}

Python

class Solution:
    def numTrees(self, n: int) -> int:
        dp = [0] * (n + 1)  # Create an array of size n+1, initialized to 0
        dp[0] = 1  # When n is 0, there is only one tree, the empty tree
        for i in range(1, n + 1):  # Iterate over each number from 1 to n
            for j in range(1, i + 1):  # Compute trees with each number i as root
                dp[i] += dp[j - 1] * dp[i - j]  # Sum combinations of left and right subtrees
        return dp[n]  # Return the total number of unique BSTs for 1 to n

Go

func numTrees(n int) int {
	dp := make([]int, n+1)
	dp[0] = 1
	for i := 1; i <= n; i++ {
		for j := 1; j <= i; j++ {
			dp[i] += dp[j-1] * dp[i-j]
		}
	}
	return dp[n]
}

JavaScript

const numTrees = (n) => {
    let dp = new Array(n+1).fill(0);
    dp[0] = 1;
    dp[1] = 1;

    for(let i = 2; i <= n; i++) {
        for(let j = 1; j <= i; j++) {
            dp[i] += dp[j-1] * dp[i-j];
        }
    }

    return dp[n];
};

TypeScript

function numTrees(n: number): number {
    const dp: number[] = [];
    dp[0] = -1; // Signifies meaningless
    dp[1] = 1;
    for (let i = 2; i <= n; i++) {
        dp[i] = 2 * dp[i - 1];
        for (let j = 1, end = i - 1; j < end; j++) {
            dp[i] += dp[j] * dp[end - j];
        }
    }
    return dp[n];
};

Rust

impl Solution {
    pub fn num_trees(n: i32) -> i32 {
        let n = n as usize;
        let mut dp = vec![0; n + 1];
        dp[0] = 1;
        for i in 1..=n {
            for j in 1..=i {
                dp[i] += dp[j - 1] * dp[i - j];
            }
        }
        dp[n]
    }
}

C

int *initDP(int n) {
    int *dp = (int *)malloc(sizeof(int) * (n + 1));
    int i;
    for(i = 0; i <= n; ++i)
        dp[i] = 0;
    return dp;
}

int numTrees(int n) {
    int *dp = initDP(n);
    dp[0] = 1;

    int i, j;
    for(i = 1; i <= n; ++i) {
        for(j = 1; j <= i; ++j) {
            dp[i] += dp[j - 1] * dp[i - j];
        }
    }

    return dp[n];
}

Scala

object Solution {
  def numTrees(n: Int): Int = {
    var dp = new Array[Int](n + 1)
    dp(0) = 1
    for (i <- 1 to n) {
      for (j <- 1 to i) {
        dp(i) += dp(j - 1) * dp(i - j)
      }
    }
    dp(n)
  }
}

C#

public class Solution
{
    public int NumTrees(int n)
    {
        int[] dp = new int[n + 1];
        dp[0] = 1;
        for (int i = 1; i <= n; i++)
        {
            for (int j = 1; j <= i; j++)
            {
                dp[i] += dp[j - 1] * dp[i - j];
            }
        }
        return dp[n];
    }
}