968. Binary Tree Cameras

LeetCode Problem Link (opens new window)

Given a binary tree, we install cameras on the tree nodes.

Each camera at a node can monitor its parent, itself, and its immediate children.

Calculate the minimum number of cameras needed to monitor all nodes of the tree.

Example 1:

• Input: [0,0,null,0,0]
• Output: 1
• Explanation: As shown in the figure, one camera is enough to monitor all nodes.

Example 2:

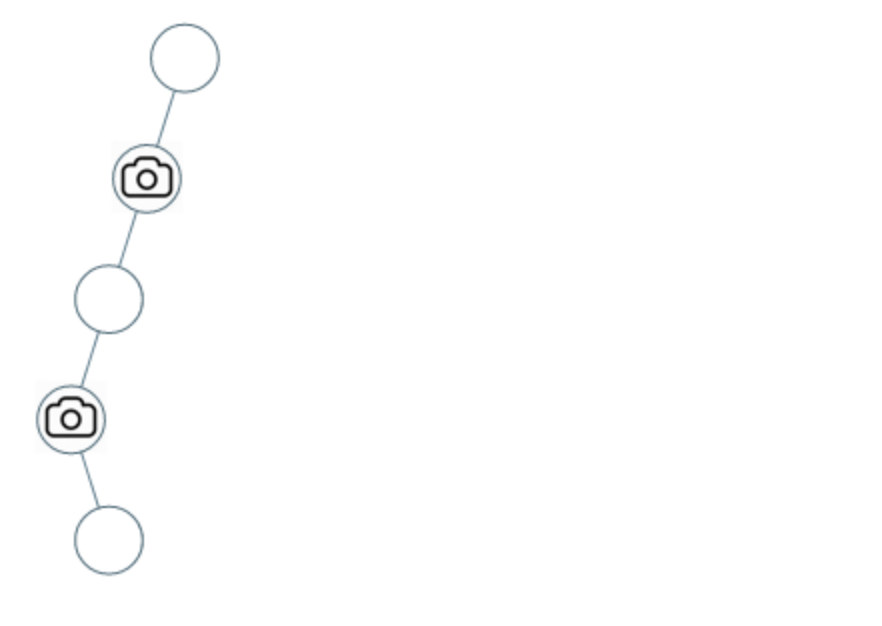
• Input: [0,0,null,0,null,0,null,null,0]
• Output: 2
• Explanation: At least two cameras are needed to monitor all nodes. The figure shows one possible position for the cameras.

Constraints:

• The number of nodes in the given tree is in the range [1, 1000].
• Each node's value is 0.

Approach

First, consider how to place cameras to minimize their number.

From the examples in the problem, we can infer the strategy: we observe that cameras are never placed on the leaf nodes!

This is an important clue, as a camera can cover three layers - top, middle, and bottom. Placing a camera on a leaf node wastes one layer of coverage.

Therefore, placing a camera on the parent of a leaf node maximizes the coverage.

Some might wonder why we start from the leaf nodes instead of the root node. The reason is that placing a camera at the root saves only one camera, while placing it on the parent of a leaf node saves an exponential number of cameras.

Thus, we should look at it from the bottom up with local optimum strategy: place a camera at the parent node of a leaf node to use the least amount of cameras, leading to a global optimum of the minimum number of cameras.

If the local optimum leads to the global optimum with no counterexamples, then we proceed with a greedy approach.

The primary idea is to move bottom-up, placing a camera at the parent of each leaf node, and then positioning cameras every two nodes up to the root.

Now, the problem has two main challenges:

1. Binary tree traversal
2. How to place a camera every two nodes

Determine Traversal Order

How do we derive from the bottom to the top in a binary tree?

We can use post-order traversal, which follows the order of left, right, and then current node, allowing us to work our way up the tree during the backtracking process.

The post-order traversal code is as follows:

int traversal(TreeNode* cur) {
    // Empty node, this node is covered
    if (termination condition) return;
    int left = traversal(cur->left);    // Left
    int right = traversal(cur->right);  // Right
    Logic processing                       // Current
    return;
}

Notice that in the above code, we take the return values of the left and right children, i.e., left and right, which we will use to derive the state of the current node.

How to Place a Camera Every Two Nodes

Now it's necessary to derive the state transition formula, and note that, unlike dynamic programming, there is no process of selection, just pure state transition!

Let's consider how many states a node can have:

There are the following three:

• The node is not covered
• The node has a camera
• The node is covered

We represent them with three numbers:

• 0: The node is not covered
• 1: The node has a camera
• 2: The node is covered

You probably can't find a fourth state different from these.

Some might wonder if there's a fourth state: the node without a camera. In fact, without the camera means it falls under either the not covered or covered state, so there are still just the three states.

Because during the traversal of the tree we'll encounter empty nodes, the question arises: what state should empty nodes be in? Should an empty node represent not covered, have a camera, or be covered?

Returning to the essence, to minimize the number of cameras, we should place cameras on the parent nodes of leaves so that we can use the least number of cameras.

Therefore, empty nodes cannot be in the "not covered" state; otherwise, cameras would have to be placed on the leaf nodes. Empty nodes also cannot be in the "has camera" state because then cameras would not need to be placed on the parents of the leaves, but could instead be placed on the grandparents of the leaves.

Therefore, the state of empty nodes can only be "covered," allowing for cameras to be placed on the parent nodes of leaves.

Next is the recursive relationship.

The termination condition for recursion should be when an empty node is encountered and should return 2 (covered state), as explained above.

The code is as follows:

// Empty node, this node is covered
if (cur == NULL) return 2;

The recursive function and termination conditions have been established, so let’s look at the logic for a single layer.

There are primarily four situations:

• Case 1: Both left and right nodes are covered

The left child is covered, the right child is covered, and thus the middle node would be in the "not covered" state.

For example:

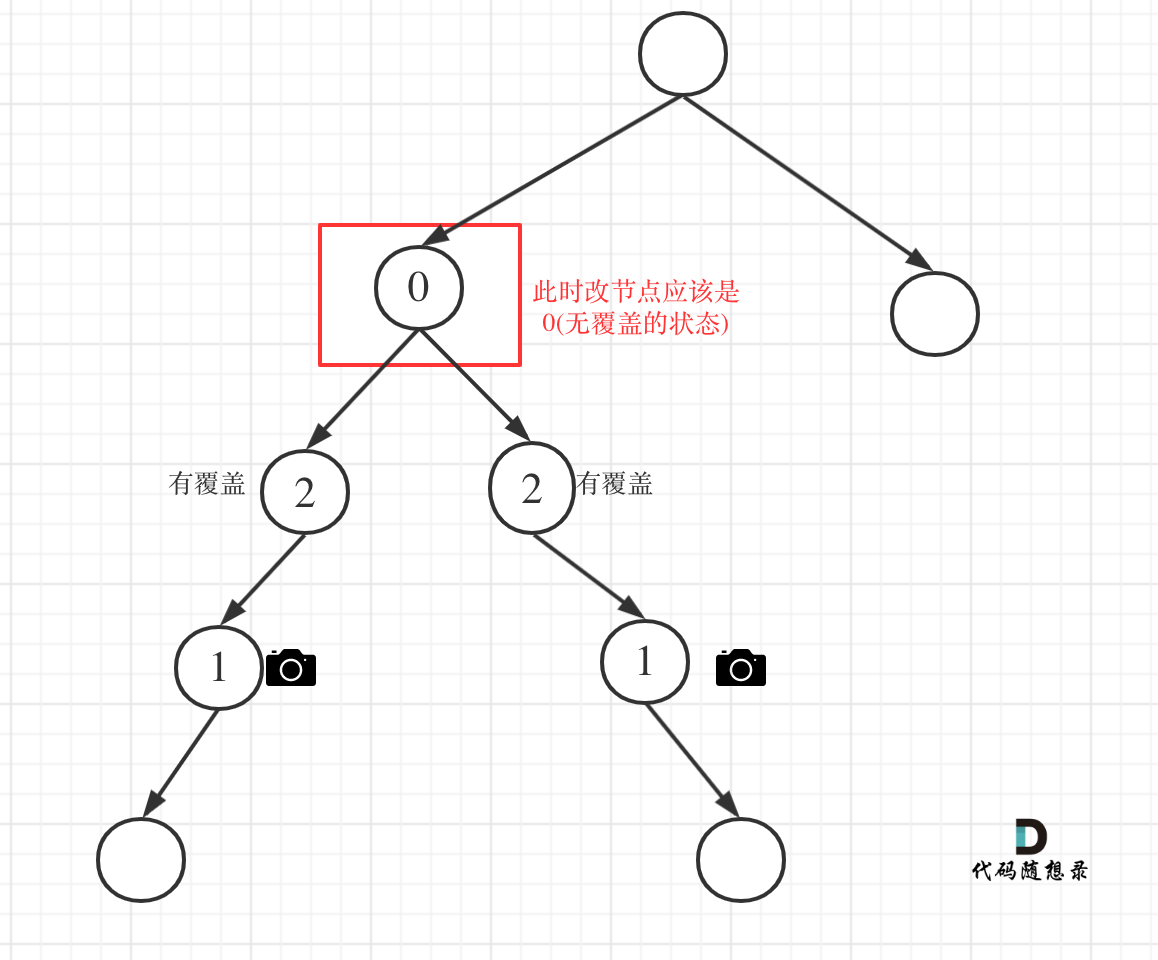
The code is:

// Both left and right nodes are covered
if (left == 2 && right == 2) return 0;

• Case 2: At least one of the left or right nodes is not covered

In such cases, the middle node (parent node) should have a camera:

• left == 0 && right == 0: Both left and right nodes are not covered
• left == 1 && right == 0: Left node has a camera; right node is not covered
• left == 0 && right == 1: Left node is not covered; right node has a camera
• left == 0 && right == 2: Left node is not covered; right node is covered
• left == 2 && right == 0: Left node is covered; right node is not covered

This is logical because if a child is not covered, the parent node should have a camera.

At this point, increment the count of cameras, and return 1 to indicate the middle node has a camera.

The code is:

if (left == 0 || right == 0) {
    result++;
    return 1;
}

• Case 3: At least one of the left or right nodes has a camera

In such cases, if one of the following is true, it means one child node already has a camera, so the parent node should be in the "covered" state (2):

• left == 1 && right == 2: Left node has a camera; right node is covered
• left == 2 && right == 1: Left node is covered; right node has a camera
• • left == 1 && right == 1: Both left and right nodes have cameras

The code is:

if (left == 1 || right == 1) return 2;

In this code, we see that if left == 1, right == 0, the condition will already be checked in case 2, as shown in the illustration:

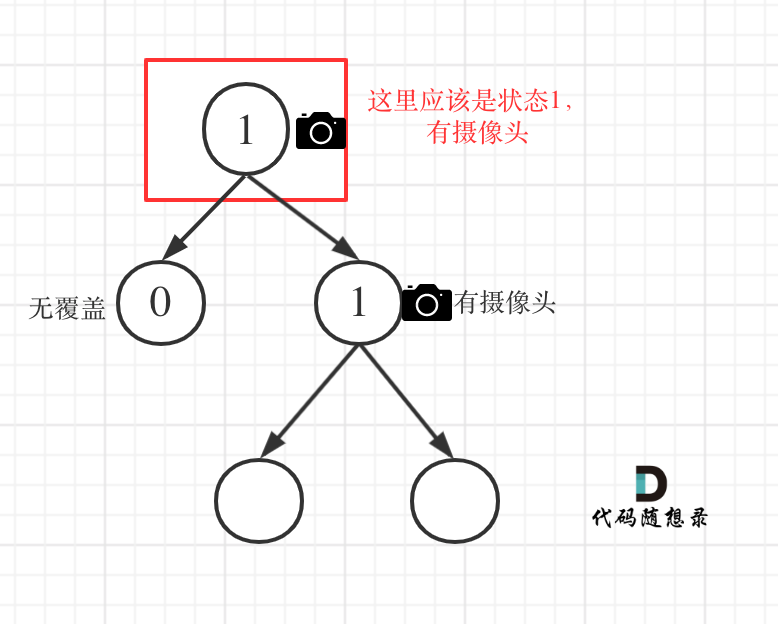
This situation is one many users might find confusing.

4. Case 4: Root node not covered

After completing the checks and ending the recursion, there could be a situation where the root node is still not covered, as shown:

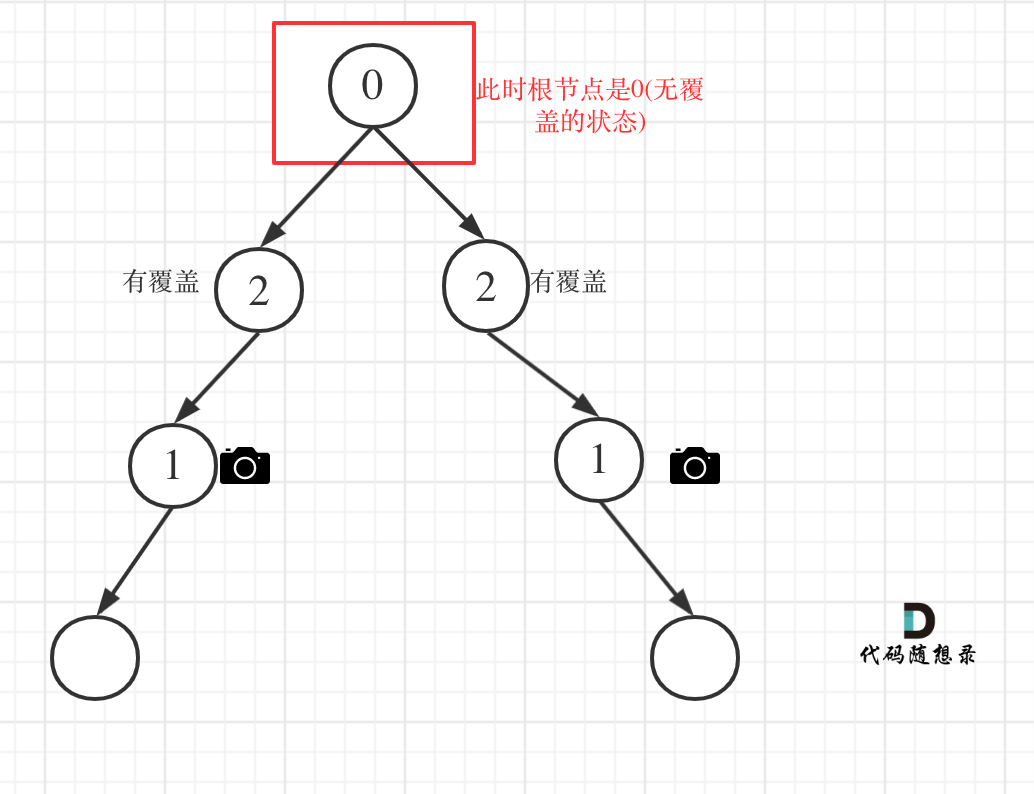
So after the recursion ends, we need to check the root node, and if it’s not covered, result++. The code is:

int minCameraCover(TreeNode* root) {
    result = 0;
    if (traversal(root) == 0) { // root not covered
        result++;
    }
    return result;
}

After analyzing all four situations, here is the complete code:

(Below I have detailed comments for the code. To clarify the cases, I specifically listed each one.)

C++ code:

// Version 1
class Solution {
private:
    int result;
    int traversal(TreeNode* cur) {
        // Empty node, this node is covered
        if (cur == NULL) return 2;
        int left = traversal(cur->left);    // Left
        int right = traversal(cur->right);  // Right

        // Case 1: Both left and right nodes are covered
        if (left == 2 && right == 2) return 0;

        // Case 2: At least one of the left or right nodes is not covered
        if (left == 0 || right == 0) {
            result++;
            return 1;
        }

        // Case 3: At least one of the left or right nodes has a camera
        if (left == 1 || right == 1) return 2;

        // In the code above, I did not use else, mainly to show each branch condition. It makes the code easier to understand
        // This return -1 logic will not be reached.
        return -1;
    }

public:
    int minCameraCover(TreeNode* root) {
        result = 0;
        // Case 4: Root not covered
        if (traversal(root) == 0) { // root not covered
            result++;
        }
        return result;
    }
};

Following the above code, we can simplify it as follows:

// Version 2
class Solution {
private:
    int result;
    int traversal(TreeNode* cur) {
        if (cur == NULL) return 2;
        int left = traversal(cur->left);    // Left
        int right = traversal(cur->right);  // Right
        if (left == 2 && right == 2) return 0;
        else if (left == 0 || right == 0) {
            result++;
            return 1;
        } else return 2;
    }
public:
    int minCameraCover(TreeNode* root) {
        result = 0;
        if (traversal(root) == 0) { // root not covered
            result++;
        }
        return result;
    }
};

• Time complexity: O(n), as each node in the binary tree needs to be traversed.
• Space complexity: O(n)

You may find it surprising that it can be reduced to such concise code. In fact, it's just using else to directly cover some conditions in version one.

There are many such concise solutions available online for this problem, but without a detailed explanation, they're hard to understand—a direct look at the code could make it even more confusing. Hence, it's recommended to follow along with the code in Version 1 step-by-step, as Version 2 is not as illuminating.

Conclusion

The difficulty in this problem begins with thinking of a greedy solution and continues through the process of traversing and deducing the state.

Deriving the state in a binary tree raises the level of complexity quite a bit, requiring a good mastery of binary tree operations.

As an officially recognized hard problem, experiencing it will surely be insightful.

Additional Language Versions

Java

class Solution {
    int  res=0;
    public int minCameraCover(TreeNode root) {
        // Check the state of the root node to ensure it is not uncovered.
        if(minCame(root)==0){
            res++;
        }
        return res;
    }
    /**
     Node state values:
       0 indicates uncovered
       1 indicates with a camera
       2 indicates covered
    Post-order traversal, determine the state according to the left and right nodes.
     */
    public int minCame(TreeNode root){
        if(root==null){
            // Null nodes are considered covered to avoid placing cameras on leaf nodes
            return 2;
        }
        int left=minCame(root.left);
        int  right=minCame(root.right);

        // If both left and right nodes are covered, set the state of the root node to uncovered
        if(left==2&&right==2){
            //(2,2)
            return 0;
        }else if(left==0||right==0){
            // If both nodes are uncovered, place a camera on the root node
            // (0,0) (0,1) (0,2) (1,0) (2,0)
            // State value 1, increment camera count
            res++;
            return 1;
        }else{
            // If nodes have states (1,1) (1,2) (2,1), meaning at least one child has a camera,
            // then the root node is in a covered state.
            return 2;
        }
    }
}

Simplified branches version:

class Solution {
    static int ans;
    public int minCameraCover(TreeNode root) {
        ans = 0; // Initialize
        if(f(root) == 0) ans ++;
        return ans;
    }
    // Define function f with three types of return values
    // 0: Indicates node x is not monitored, requiring the parent node to have a camera
    // 1: Indicates node x is monitored, but camera is not at the node itself
    // 2: Indicates node x is monitored, with a camera at the node itself
    public static int f(TreeNode x) {
        if(x == null) return 1; // Null tree is considered monitored without a camera
        // Recurse to the deepest
        int l = f(x.left);
        int r = f(x.right);
        // If any child node is null, the current node needs a camera, otherwise no opportunity
        if(l == 0 || r == 0) {
            ans ++; // Place camera
            return 2;
        }
        // Strategy: if both children are monitored but not monitoring the current node,
        // the best situation is to place the camera at the parent node,
        // so it can monitor additional potential child and grandparent nodes
        if(l == 1 && r == 1) return 0;
        // Remaining case: children could be 2, meaning current node is monitored
        return 1; 
    }
}

Python

Greedy (version 1)

class Solution:
    # Greedy Algorithm:
    # Install cameras from the bottom-up, skipping leaves for minimal number placement with local-to-global optimization
    # Install at the parent of leaves first, then continue every two levels up to the root
    # 0: Node is not covered
    # 1: Node has a camera
    # 2: Node is covered
    def minCameraCover(self, root: TreeNode) -> int:
        # Define recursive function
        result = [0]  # To keep track of the number of cameras installed
        if self.traversal(root, result) == 0:
            result[0] += 1
        return result[0]

    def traversal(self, cur: TreeNode, result: List[int]) -> int:
        if not cur:
            return 2

        left = self.traversal(cur.left, result)
        right = self.traversal(cur.right, result)

        # Case 1: Both left and right nodes are covered
        if left == 2 and right == 2:
            return 0

        # Case 2:
        # left == 0 && right == 0: Both nodes are uncovered
        # left == 1 && right == 0: Left has a camera; right is uncovered
        # left == 0 && right == 1: Left is uncovered; right has a camera
        # left == 0 && right == 2: Left is uncovered; right is covered
        # left == 2 && right == 0: Left is covered; right is uncovered
        if left == 0 or right == 0:
            result[0] += 1
            return 1

        # Case 3:
        # left == 1 && right == 2: Left has a camera; right is covered
        # left == 2 && right == 1: Left is covered; right has a camera
        # left == 1 && right == 1: Both left and right have cameras
        if left == 1 or right == 1:
            return 2

Greedy (version 2) using elif to simplify code

class Solution:
    # Greedy Algorithm:
    # Install cameras from the bottom-up, skipping leaves for minimal number placement with local-to-global optimization
    # Install at the parent of leaves first, then continue every two levels up to the root
    # 0: Node is not covered
    # 1: Node has a camera
    # 2: Node is covered
    def minCameraCover(self, root: TreeNode) -> int:
        # Define recursive function
        result = [0]  # To keep track of the number of cameras installed
        if self.traversal(root, result) == 0:
            result[0] += 1
        return result[0]

    def traversal(self, cur: TreeNode, result: List[int]) -> int:
        if not cur:
            return 2

        left = self.traversal(cur.left, result)
        right = self.traversal(cur.right, result)

        # Case 1: Both left and right nodes are covered
        if left == 2 and right == 2:
            return 0

        # Case 2:
        # left == 0 && right == 0: Both nodes are uncovered
        # left == 1 && right == 0: Left has a camera; right is uncovered
        # left == 0 && right == 1: Left is uncovered; right has a camera
        # left == 0 && right == 2: Left is uncovered; right is covered
        # left == 2 && right == 0: Left is covered; right is uncovered
        elif left == 0 or right == 0:
            result[0] += 1
            return 1

        # Case 3:
        # left == 1 && right == 2: Left has a camera; right is covered
        # left == 2 && right == 1: Left is covered; right has a camera
        # left == 1 && right == 1: Both left and right have cameras
        else:
            return 2

Go

const inf = math.MaxInt64 / 2

func minCameraCover(root *TreeNode) int {
    var dfs func(*TreeNode) (a, b, c int)
    dfs = func(node *TreeNode) (a, b, c int) {
        if node == nil {
            return inf, 0, 0
        }
        lefta, leftb, leftc := dfs(node.Left)
        righta, rightb, rightc := dfs(node.Right)
        a = leftc + rightc + 1
        b = min(a, min(lefta+rightb, righta+leftb))
        c = min(a, leftb+rightb)
        return
    }
    _, ans, _ := dfs(root)
    return ans
}

func min(a, b int) int {
    if a <= b {
        return a
    }
    return b
}

JavaScript

var minCameraCover = function(root) {
    let result = 0
    function traversal(cur) {
        if(cur === null) {
            return 2
        }

        let left = traversal(cur.left)
        let right = traversal(cur.right)

        if(left === 2 && right === 2) {
            return 0
        }

        if(left === 0 || right === 0) {
            result++
            return 1
        }

        if(left === 1 || right === 1) {
            return 2
        }

        return -1
    }

    if(traversal(root) === 0) {
        result++
    }

    return result
}

TypeScript

function minCameraCover(root: TreeNode | null): number {
    /** 0-Not Covered, 1-Has Camera, 2-Covered */
    type statusCode = 0 | 1 | 2;
    let resCount: number = 0;
    if (recur(root) === 0) resCount++;
    return resCount;
    function recur(node: TreeNode | null): statusCode {
        if (node === null) return 2;
        const left: statusCode = recur(node.left),
            right: statusCode = recur(node.right);
        let resStatus: statusCode = 0;
        if (left === 0 || right === 0) {
            resStatus = 1;
            resCount++;
        } else if (left === 1 || right === 1) {
            resStatus = 2;
        } else {
            resStatus = 0;
        }
        return resStatus;
    }
};

C

/*
**Function post-order traverses the binary tree. In determining a node's state, it is based on the states of its left and right child nodes.
**State: 0 means uncovered, 1 means the node has a camera, 2 means the node is covered.
*/
int traversal(struct TreeNode* node, int* ans) {
    // Recursive termination condition: pass in a NULL node, assume this node can be covered by a camera, to make the leaf node 0.
    if(!node)
        return 2;
    // Post-order traverse the binary tree, recording the states of the left and right children, updating the state of the node based on these.
    int left = traversal(node->left, ans);
    int right = traversal(node->right, ans);

    // If both the left and right nodes are covered, set the parent node state to 0.
    if(left == 2 && right == 2) {
        return 0; // Uncovered
    }

    // If either of the child nodes is uncovered (0), parent node should have a camera
    if(left == 0 || right == 0) {
        (*ans)++;
        return 1; // Camera placed
    }

    // If either child has a camera (1), or both children are covered by a camera, parent is covered
    if(left == 1 || right == 1)
        return 2;
    // Logic will not reach this return -1, code won't execute
    return -1;
}

int minCameraCover(struct TreeNode* root){
    int ans = 0;

    // After traversing the entire binary tree, the root node might still be uncovered, in which case if function return 0, it needs a camera.
    if(traversal(root, &ans) == 0)
        ans++;
    return ans;
}

Scala

object Solution {
  def minCameraCover(root: TreeNode): Int = {
    var result = 0
    def traversal(cur: TreeNode): Int = {
      // Empty node, this node is covered
      if (cur == null) return 2
      val left = traversal(cur.left)
      val right = traversal(cur.right)
      // Case 1, both left and right nodes are covered
      if (left == 2 && right == 2) {
        return 0
      }
      // Case 2
      if (left == 0 || right == 0) {
        result += 1
        return 1
      }
      // Case 3
      if (left == 1 || right == 1) {
        return 2
      }
      -1
    }

    if (traversal(root) == 0) {
      result += 1
    }
    result
  }
}

Rust

/// Version 1
impl Solution {
    pub fn min_camera_cover(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
        let mut res = 0;
        if Self::traversal(&root, &mut res) == 0 {
            res += 1;
        }
        res
    }

    pub fn traversal(cur: &Option<Rc<RefCell<TreeNode>>>, ans: &mut i32) -> i32 {
        // 0 Not covered, 1 Node with camera, 2 Node covered
        if let Some(node) = cur {
            let node = node.borrow();

            let left = Self::traversal(&node.left, ans);
            let right = Self::traversal(&node.right, ans);

            // Both children are covered, return 0
            if left == 2 && right == 2 {
                return 0; // Uncovered
            }

            // Whether one or both children are uncovered (0), need a camera
            if left == 0 || right == 0 {
                *ans += 1;
                return 1;
            }

            // Case: (1,2) (2,1) (1,1) base on children status, parents is covered
            if left == 1 || right == 1 {
                return 2; // Covered
            }
        } else {
            return 2;
        }
        -1
    }
}

/// Version 2
enum NodeState {
    NoCover = 0,
    Camera = 1,
    Covered = 2,
}

impl Solution {
    pub fn min_camera_cover(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
        let mut res = 0;
        let state = Self::traversal(&root, &mut res);
        match state {
            NodeState::NoCover => res + 1,
            _ => res,
        }
    }

    pub fn traversal(cur: &Option<Rc<RefCell<TreeNode>>>, ans: &mut i32) -> NodeState {
        if let Some(node) = cur {
            let node = node.borrow();
            let left_state = Self::traversal(&node.left, ans);
            let right_state = Self::traversal(&node.right, ans);
            match (left_state, right_state) {
                (NodeState::NoCover, _) | (_, NodeState::NoCover) => {
                    *ans += 1;
                    NodeState::Camera
                }
                (NodeState::Camera, _) | (_, NodeState::Camera) => NodeState::Covered,
                (_, _) => NodeState::NoCover,
            }
        } else {
            NodeState::Covered
        }
    }
}

C#

public class Solution
{
    public int res = 0;
    public int MinCameraCover(TreeNode root)
    {
        if (Traversal(root) == 0) res++;
        return res;
    }
    public int Traversal(TreeNode cur)
    {
        if (cur == null) return 2;
        int left = Traversal(cur.left);
        int right = Traversal(cur.right);
        if (left == 2 && right == 2) return 0;
        else if (left == 0 || right == 0)
        {
            res++;
            return 1;
        }
        else return 2;
    }
}