131.Palindrome Partitioning

LeetCode Problem Link (opens new window)

Given a string s, partition s such that every substring of the partition is a palindrome.

Return all possible palindrome partitioning of s.

Example: Input: "aab"
Output: [ ["aa","b"], ["a","a","b"] ]

Approach

This problem involves two key issues:

1. The problem of partitioning, which involves multiple partitioning methods.
2. Determining palindromes.

The variety of partitioning methods can be confusing for many students.

Attempting a brute force solution with for-loops might be challenging, so a different brute force approach, backtracking, should be considered.

Some students might struggle with understanding how to partition the string with backtracking.

Let's analyze the partitioning. Partitioning problems are similar to combination problems.

For example, for the string "abcdef":

• In combination problems: After selecting one element, say a, then selecting the second from bcdef, and selecting b then selecting the third from cdef, and so on.
• In partitioning problems: After partitioning one element, say a, then partition the second from bcdef, and after partitioning b, partition the third from cdef, and so on.

Can you sense the similarity?

Therefore, partitioning problems can also be abstracted into a tree structure, as shown below:

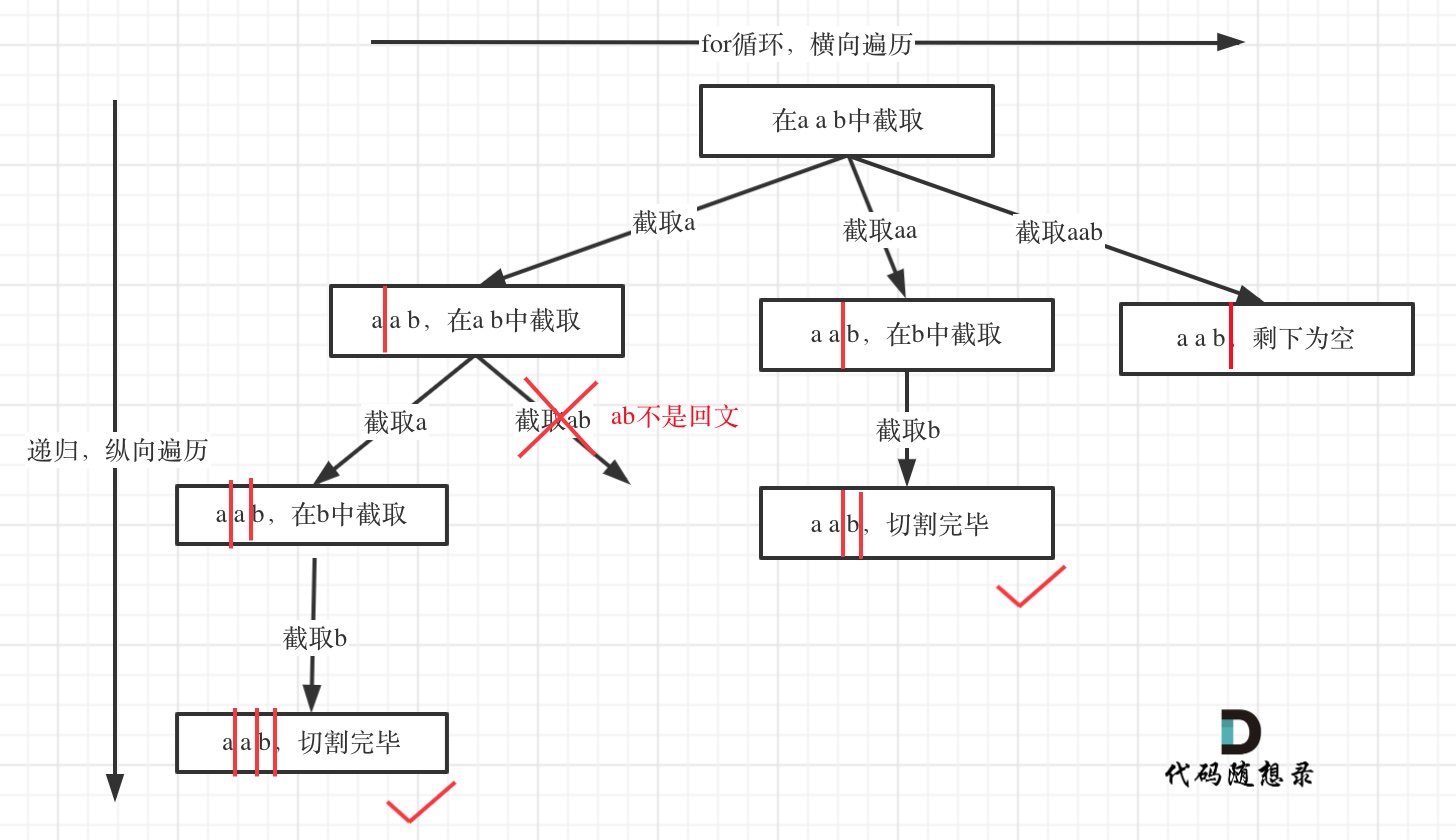
Recursion is used to traverse vertically, and for-loops are used to traverse horizontally. When the partitioning line (the red lines in the diagram) reaches the end of the string, it means a way of partitioning has been found.

It’s noticeable that the recursive search process of partitioning problems is quite similar to the recursive search process of combination problems.

Three Steps of Backtracking

• Recursive Function Parameters

A global variable array path stores the palindromic substrings after partitioning, and a two-dimensional array result stores the set of results. (These two parameters can be included in the function parameters)

The recursive function parameters for this problem also need a startIndex because once cut, you shouldn't repeat cutting the same place, similar to combination problems.

As discussed in 0039. Combination Sum (opens new window), we delved into when the startIndex is required for combination problems.

The code is as follows:

vector<vector<string>> result;
vector<string> path; // Stores already palindromic substrings
void backtracking (const string& s, int startIndex) {

• Base Condition for Recursive Function

From the tree diagram, it’s shown that when the line partitions to the end of the string, it indicates one way of partitioning is found. This serves as the base case for recursion termination.

So, what is the partition line in the code?

In handling combination problems, recursive function parameters require passing startIndex, indicating the starting point for the next recursive traversal, and this startIndex is the partition line.

Therefore, the termination condition code is as follows:

void backtracking (const string& s, int startIndex) {
    // If the starting point is already greater than the size of `s`, a set of partitioning solutions has been found
    if (startIndex >= s.size()) {
        result.push_back(path);
        return;
    }
}

• Logic of Single-Level Search

How is the substring segment determined within the recursive loop?

In the loop for (int i = startIndex; i < s.size(); i++), the starting position is defined as startIndex, then [startIndex, i] is the segment to be truncated as a substring.

First, check if this substring is a palindrome. If it is, add it to vector<string> path, where path is used to record partitioned palindromic substrings.

The code is as follows:

for (int i = startIndex; i < s.size(); i++) {
    if (isPalindrome(s, startIndex, i)) { // Is a palindrome substring
        // Get the substring of s from [startIndex,i]
        string str = s.substr(startIndex, i - startIndex + 1);
        path.push_back(str);
    } else {                // If not, skip it
        continue;
    }
    backtracking(s, i + 1); // Look for the substring starting at i+1
    path.pop_back();        // Backtracking, pop the substring added this time
}

Note that once a position is partitioned, it cannot be partitioned again, so backtracking(s, i + 1); passes the starting point of the next layer to i + 1.

Determining Palindrome Substrings

Finally, let's look at how palindromic substrings are determined. To check if a string is a palindrome, the double pointer method can be used: one pointer moves from the front towards the back, and the other from the back towards the front. If the elements pointed to by the front and back pointers are equal, the string is a palindrome.

Then, the C++ code for determining palindromes is as follows:

 bool isPalindrome(const string& s, int start, int end) {
     for (int i = start, j = end; i < j; i++, j--) {
         if (s[i] != s[j]) {
             return false;
         }
     }
     return true;
 }

If you're unfamiliar with the double pointer method, refer to: Double Pointers Summary (opens new window)

Now, the critical code has been explained, and the complete code is as follows (with detailed comments):

Based on Carl's backtracking algorithm template:

void backtracking(params) {
    if (termination condition) {
        store result;
        return;
    }

    for (choice: each element in the current layer's collection (the number of children nodes in the tree is the size of the collection)) {
        process node;
        backtracking(path, choice list); // Recursion
        backtrack, undo processing result
    }
}

It's not difficult to write the following code:

class Solution {
private:
    vector<vector<string>> result;
    vector<string> path; // To store the substrings that are palindromes
    void backtracking (const string& s, int startIndex) {
        // If the starting position is already greater than `s` size, a partitioning solution is found.
        if (startIndex >= s.size()) {
            result.push_back(path);
            return;
        }
        for (int i = startIndex; i < s.size(); i++) {
            if (isPalindrome(s, startIndex, i)) {   // Is a palindrome substring
                // Get the substring of `s` from [startIndex, i]
                string str = s.substr(startIndex, i - startIndex + 1);
                path.push_back(str);
            } else {                                // Not a palindrome, skip it
                continue;
            }
            backtracking(s, i + 1); // Looking for the substring starting at i+1
            path.pop_back(); // Backtracking, pop the substring added in this round
        }
    }
    bool isPalindrome(const string& s, int start, int end) {
        for (int i = start, j = end; i < j; i++, j--) {
            if (s[i] != s[j]) {
                return false;
            }
        }
        return true;
    }
public:
    vector<vector<string>> partition(string s) {
        result.clear();
        path.clear();
        backtracking(s, 0);
        return result;
    }
};

• Time Complexity: O(n * 2^n)
• Space Complexity: O(n^2)

Optimization

The above code has some space for optimization, particularly in how efficiently a substring can be determined to be a palindrome. The isPalindrome function in the above code uses the double pointer method to determine if a substring is a palindrome for a given string s with specified starting and ending indexes. However, this involves some redundant calculations:

For example, given the string "abcde", when it is known that "bcd" is not a palindrome, there is no need to check "abcde" using double pointers, as it definitely isn't a palindrome.

Specifically, for a given string s of length n, a necessary and sufficient condition for it to be a palindrome is s[0] == s[n-1] and s[1:n-1] is also a palindrome.

For those familiar with the dynamic programming algorithm, we can efficiently calculate once and for all if any substring of a given string s is a palindrome, and then directly query it in our backtracking function, removing the need for double pointer checks.

The reference code is as follows:

class Solution {
private:
    vector<vector<string>> result;
    vector<string> path; // To store already palindromic substrings
    vector<vector<bool>> isPalindrome; // To store pre-calculated palindrome substring results
    void backtracking (const string& s, int startIndex) {
        // If the starting position is greater than or equal to `s` size, a partitioning solution is found.
        if (startIndex >= s.size()) {
            result.push_back(path);
            return;
        }
        for (int i = startIndex; i < s.size(); i++) {
            if (isPalindrome[startIndex][i]) {   // Is a palindrome substring
                // Get the substring of `s` from [startIndex, i]
                string str = s.substr(startIndex, i - startIndex + 1);
                path.push_back(str);
            } else {                                // Not a palindrome, skip
                continue;
            }
            backtracking(s, i + 1); // Find the substring starting at i+1
            path.pop_back(); // Backtracking, pop the substring added in this recursion
        }
    }
    void computePalindrome(const string& s) {
        // isPalindrome[i][j] represents if `s[i:j]` (both inclusive) is a palindrome
        isPalindrome.resize(s.size(), vector<bool>(s.size(), false)); // Reset the boolean matrix size according to string `s`
        for (int i = s.size() - 1; i >= 0; i--) { 
            // Needs to be calculated in reverse order, ensuring that the `i+1` row is calculated before the `i` row
            for (int j = i; j < s.size(); j++) {
                if (j == i) {isPalindrome[i][j] = true;}
                else if (j - i == 1) {isPalindrome[i][j] = (s[i] == s[j]);}
                else {isPalindrome[i][j] = (s[i] == s[j] && isPalindrome[i+1][j-1]);}
            }
        }
    }
public:
    vector<vector<string>> partition(string s) {
        result.clear();
        path.clear();
        computePalindrome(s);
        backtracking(s, 0);
        return result;
    }
};

Summary

This problem is marked as medium on Leetcode but it could be considered a hard problem. However, the code actually follows a template pattern.

What exactly makes this problem difficult?

I list the following difficulties:

• Partitioning problems can be abstracted into combination problems.
• How to simulate those partitioning lines.
• When do partitioning problems terminate in recursion?
• How to extract substrings in the recursive loop.
• How to determine palindromes.

When facing difficult problems, identifying what exactly makes them difficult is also a capability that needs to be developed.

Some students might find the problem difficult but cannot pinpoint why, just that it feels hard. This actually indicates unclear thinking, and such summarizing skills need more exposure and training.

In this problem, I believe many students mainly struggle with the first key point: not knowing how to partition, and even if aware that backtracking is needed, they still don't know how. Essentially, they haven't realized that approaching it with the combination problem mindset solves the partitioning.

Realizing this is a major breakthrough. From there, one can follow the template.

Following that, simulating the partition lines, determining the termination condition, extracting substrings, and finally checking for palindromes aren't straightforward.

About simulating the partition lines, index is a partition line determined by the previous level, and i is a new partition line the current level attempts to find.

Aside from these key points, in this problem, details matter, like not being able to repeatedly partition the same place, which is why (i + 1) is needed in the recursive function.

So, this problem could probably be a hard-level problem.

Those who have solved this problem may not have realized they overcame many key points to accomplish it, which might be called having no conscious strategy, the fusion of person and code.

Other Language Versions

Java

class Solution {
    // Maintaining the same format as the previous questions by initializing
    List<List<String>> res = new ArrayList<>();
    List<String> cur = new ArrayList<>();
    public List<List<String>> partition(String s) {
        backtracking(s, 0, new StringBuilder());
        return res;
    }
    private void backtracking(String s, int start, StringBuilder sb){
        // Since the starting position is added one by one, at the end `start` must equal `s.length`, because it is a palindrome at the end, so `cur` satisfies the condition
        if (start == s.length()){
            // Note: create a new copy
            res.add(new ArrayList<>(cur));
            return;
        }
        // Like the previous two questions, search from front to back, if a palindrome is found, enter backtracking, starting position moves back one place, at the end of the loop remove the last element of `cur`
        for (int i = start; i < s.length(); i++){
            sb.append(s.charAt(i));
            if (check(sb)){
                cur.add(sb.toString());
                backtracking(s, i + 1, new StringBuilder());
                cur.remove(cur.size() -1 );
            }
        }
    }

    // Helper method, checks if it's a palindrome
    private boolean check(StringBuilder sb){
        for (int i = 0; i < sb.length()/ 2; i++){
            if (sb.charAt(i) != sb.charAt(sb.length() - 1 - i)){return false;}
        }
        return true;
    }
}

Java

Backtracking + Dynamic Programming Optimization for Palindrome Checking

class Solution {
    List<List<String>> result;
    LinkedList<String> path;
    boolean[][] dp;

    public List<List<String>> partition(String s) {
        result = new ArrayList<>();
        char[] str = s.toCharArray();
        path = new LinkedList<>();
        dp = new boolean[str.length + 1][str.length + 1];
        isPalindrome(str);
        backtracking(s, 0);
        return result;
    }

    public void backtracking(String str, int startIndex) {
        if (startIndex >= str.length()) {
            // If the starting position is greater than `s` length, a partitioning solution is found
            result.add(new ArrayList<>(path));
            return;
        } else {
            for (int i = startIndex; i < str.length(); ++i) {
                if (dp[startIndex][i]) {
                    // Is a palindrome substring, proceed to the next recursion
                    // Save current substring into path
                    path.addLast(str.substring(startIndex, i + 1));
                    // Ensure no repetition in starting position
                    backtracking(str, i + 1);
                    path.pollLast();
                } else {
                    // Not a palindrome substring, skip
                    continue;
                }
            }
        }
    }

    // Using dynamic programming to check palindrome substrings, refer to dynamic programming: 52. Palindrome Substrings
    public void isPalindrome(char[] str) {
        for (int i = 0; i <= str.length; ++i) {
            dp[i][i] = true;
        }
        for (int i = 1; i < str.length; ++i) {
            for (int j = i; j >= 0; --j) {
                if (str[j] == str[i]) {
                    if (i - j <= 1) {
                        dp[j][i] = true;
                    } else if (dp[j + 1][i - 1]) {
                        dp[j][i] = true;
                    }
                }
            }
        }
    }
}

Python

Basic Backtracking Version

class Solution:
    def partition(self, s: str) -> List[List[str]]:
        '''
        Recursion helps to traverse vertically
        For-loop helps to traverse horizontally
        When the partition line iterates to the end of the string, it means one way is found
        Similar to combination problems, to avoid duplicate partitioning at the same position, `start_index` is needed to mark the starting position for the next round of recursion (partition line)
        '''
        result = []
        self.backtracking(s, 0, [], result)
        return result

    def backtracking(self, s, start_index, path, result ):
        # Base Case
        if start_index == len(s):
            result.append(path[:])
            return
        
        # Single Level Recursion Logic
        for i in range(start_index, len(s)):
            # A step unique to this compared to other combination problems:
            # Determine whether the substring from [start_index, i] is a palindrome
            if self.is_palindrome(s, start_index, i):
                path.append(s[start_index:i+1])
                self.backtracking(s, i+1, path, result)   # Recursion for vertical traversal: partition from the next spot, and determine the rest is still a palindrome
                path.pop()             # Backtracking

    def is_palindrome(self, s: str, start: int, end: int) -> bool:
        i: int = start        
        j: int = end
        while i < j:
            if s[i] != s[j]:
                return False
            i += 1
            j -= 1
        return True 

Backtracking + Optimized Palindrome Determination Function

class Solution:
    def partition(self, s: str) -> List[List[str]]:
        result = []
        self.backtracking(s, 0, [], result)
        return result

    def backtracking(self, s, start_index, path, result ):
        # Base Case
        if start_index == len(s):
            result.append(path[:])
            return
        
        # Single Level Recursion Logic
        for i in range(start_index, len(s)):
            # If the reverse and forward are the same, it means it's a palindrome
            if s[start_index: i + 1] == s[start_index: i + 1][::-1]:
                path.append(s[start_index:i+1])
                self.backtracking(s, i+1, path, result)   # Recursive vertical traversal: partition from the next spot, and judge the rest is still a palindrome
                path.pop()             # Backtracking

Backtracking + Efficient Palindrome Substring Determination

class Solution:
    def partition(self, s: str) -> List[List[str]]:
        result = []
        isPalindrome = [[False] * len(s) for _ in range(len(s))]  # Initialize isPalindrome matrix
        self.computePalindrome(s, isPalindrome)
        self.backtracking(s, 0, [], result, isPalindrome)
        return result

    def backtracking(self, s, startIndex, path, result, isPalindrome):
        if startIndex >= len(s):
            result.append(path[:])
            return

        for i in range(startIndex, len(s)):
            if isPalindrome[startIndex][i]:   # Is a palindrome substring
                substring = s[startIndex:i + 1]
                path.append(substring)
                self.backtracking(s, i + 1, path, result, isPalindrome)  # Find the substring starting at i+1
                path.pop()           # Backtracking, pop the substring added this time

    def computePalindrome(self, s, isPalindrome):
        for i in range(len(s) - 1, -1, -1):  # Needs to be calculated in reverse, ensuring that the `i+1` row is computed before the `i` row
            for j in range(i, len(s)):
                if j == i:
                    isPalindrome[i][j] = True
                elif j - i == 1:
                    isPalindrome[i][j] = (s[i] == s[j])
                else:
                    isPalindrome[i][j] = (s[i] == s[j] and isPalindrome[i+1][j-1])

Backtracking + Using all Function to Determine Palindrome Substring

class Solution:
    def partition(self, s: str) -> List[List[str]]:
        result = []
        self.partition_helper(s, 0, [], result)
        return result

    def partition_helper(self, s, start_index, path, result):
        if start_index == len(s):
            result.append(path[:])
            return

        for i in range(start_index + 1, len(s) + 1):
            sub = s[start_index:i]
            if self.isPalindrome(sub):
                path.append(sub)
                self.partition_helper(s, i, path, result)
                path.pop()

    def isPalindrome(self, s):
        return all(s[i] == s[len(s) - 1 - i] for i in range(len(s) // 2))

Go

Basic Backtracking Version

var (
    path []string  // To store already palindromic substrings
    res  [][]string
)

func partition(s string) [][]string {
    path, res = make([]string, 0), make([][]string, 0)
    dfs(s, 0)
    return res
}

func dfs(s string, start int) {
    if start == len(s) { // If the starting point equals `s` size, a partitioning solution is found
        tmp := make([]string, len(path))
        copy(tmp, path)
        res = append(res, tmp)
        return 
    }
    for i := start; i < len(s); i++ {
        str := s[start : i+1]
        if isPalindrome(str) {   // Is a palindrome substring
            path = append(path, str)
            dfs(s, i+1)         // Find the substring starting at i+1
            path = path[:len(path)-1]  // Backtracking, pop the last element added this time
        }
    }
}

func isPalindrome(s string) bool {
    for i, j := 0, len(s)-1; i < j; i, j = i+1, j-1 {
        if s[i] != s[j] {
            return false
        }
    }
    return true
}

Backtracking + Dynamic Programming Optimization for Palindrome Checking

var (
    result [][]string
    path []string // To store already palindromic substrings
    isPalindrome [][]bool // To store pre-calculated palindrome substring results
)

func partition(s string) [][]string {
    result = make([][]string, 0)
    path = make([]string, 0)
    computePalindrome(s)
    backtracing(s, 0)
    return result
}

func backtracing(s string, startIndex int) {
    // If the starting position is greater than or equal to `s` size, a partitioning solution is found
    if startIndex >= len(s) {
        tmp := make([]string, len(path))
        copy(tmp, path)
        result = append(result, tmp)
        return
    }
    for i := startIndex; i < len(s); i++ {
        if isPalindrome[startIndex][i] { // Is a palindrome substring
            // Get the substring of `s` from [startIndex, i]
            path = append(path, s[startIndex:i+1])
        } else { // Not a palindrome, skip
            continue
        }
        backtracing(s, i + 1) // Find the substring starting at i+1
        path = path[:len(path)-1] // Backtracking, pop the last element added this time
    }
}

func computePalindrome(s string) {
    // isPalindrome[i][j] represents if `s[i:j]` (both inclusive) is a palindrome 
    isPalindrome = make([][]bool, len(s))
    for i := 0; i < len(isPalindrome); i++ {
        isPalindrome[i] = make([]bool, len(s))
    }
    for i := len(s)-1; i >= 0; i-- {
        // Needs to be calculated in reverse, ensuring that the `i+1` row is computed before the `i` row
        for j := i; j < len(s); j++ {
            if j == i {
                isPalindrome[i][j] = true
            } else if j - i == 1 {
                isPalindrome[i][j] = s[i] == s[j]
            } else {
                isPalindrome[i][j] = s[i] == s[j] && isPalindrome[i+1][j-1]
            }
        }
    }
}

JavaScript

/**
 * @param {string} s
 * @return {string[][]}
 */
const isPalindrome = (s, l, r) => {
    for (let i = l, j = r; i < j; i++, j--) {
        if(s[i] !== s[j]) return false;
    }
    return true;
}

var partition = function(s) {
    const res = [], path = [], len = s.length;
    backtracking(0);
    return res;
    function backtracking(startIndex) {
        if(startIndex >= len) {
            res.push(Array.from(path));
            return;
        }
        for(let i = startIndex; i < len; i++) {
            if(!isPalindrome(s, startIndex, i)) continue;
            path.push(s.slice(startIndex, i + 1));
            backtracking(i + 1);
            path.pop();
        }
    }
};

TypeScript

function partition(s: string): string[][] {
    const res: string[][] = []
    const path: string[] = []
    const isHuiwen = (
        str: string, 
        startIndex: number, 
        endIndex: number
        ): boolean => {
        for (; startIndex < endIndex; startIndex++, endIndex--) {
            if (str[startIndex] !== str[endIndex]) {
                return false
            }
        }
        return true
    }
    const rec = (str: string, index: number): void => {
        if (index >= str.length) {
            res.push([...path])
            return
        }
        for (let i = index; i < str.length; i++) {
            if (!isHuiwen(str, index, i)) {
               continue
            }
            path.push(str.substring(index, i + 1))
            rec(str, i + 1)
            path.pop()
        }
    }
    rec(s, 0)
    return res
};

C

char** path;
int pathTop;
char*** ans;
int ansTop = 0;
int* ansSize;

// Copy all strings in path to ans
void copy() {
    // Create a temporary tempPath to store strings in path
    char** tempPath = (char**)malloc(sizeof(char*) * pathTop);
    int i;
    for(i = 0; i < pathTop; i++) {
        tempPath[i] = path[i];
    }
    // Store tempPath
    ans[ansTop] = tempPath;
    // Store the current path's length (pathTop) in ansSize
    ansSize[ansTop++] = pathTop;
}

// Determine if a string is a palindrome
bool isPalindrome(char* str, int startIndex, int endIndex) {
    // Double pointer method: proceed while the endIndex (right pointer) is greater than the startIndex (left pointer)
    while(endIndex >= startIndex) {
        // If the elements pointed by left and right pointers are not the same, return false
        if(str[endIndex--] != str[startIndex++])
            return 0;
    }
    return 1;
}

// Cut the substring from startIndex to endIndex
char* cutString(char* str, int startIndex, int endIndex) {
    // Allot space for the string
    char* tempString = (char*)malloc(sizeof(char) * (endIndex - startIndex + 2));
    int i;
    int index = 0;
    // Copy the substring
    for(i = startIndex; i <= endIndex; i++)
        tempString[index++] = str[i];
    // Use '\0' to mark the end of the string
    tempString[index] = '\0';
    return tempString;
}

void backTracking(char* str, int strLen, int startIndex) {
    if(startIndex >= strLen) {
        // Copy path to ans
        copy();
        return ;
    }

    int i;
    for(i = startIndex; i < strLen; i++) {
        // If the substring from subString to i is a palindrome, add it to path
        if(isPalindrome(str, startIndex, i)) {
            path[pathTop++] = cutString(str, startIndex, i);
        }
        // If the substring from startIndex to i is not a palindrome, skip this layer 
        else {
            continue;
        }
        // Recursively check the next layer
        backTracking(str, strLen, i + 1);
        // Backtrack, pop the last element in path
        pathTop--;
    }
}

char*** partition(char* s, int* returnSize, int** returnColumnSizes){
    int strLen = strlen(s);
    // As the number of strings in path is not more than strLen (i.e., each character as a palindrome), thus allocate strLen of type char* space
    path = (char**)malloc(sizeof(char*) * strLen);
    // Store the array result in path
    ans = (char***)malloc(sizeof(char**) * 40000);
    // Store the length of each char** array in ans
    ansSize = (int*)malloc(sizeof(int) * 40000);
    ansTop = pathTop = 0;

    // Backtracking function
    backTracking(s, strLen, 0);

    // Set ansTop as the length of the ans array
    *returnSize = ansTop;
    // Set the length of each array in the ans array
    *returnColumnSizes = (int*)malloc(sizeof(int) * ansTop);
    int i;
    for(i = 0; i < ansTop; ++i) {
        (*returnColumnSizes)[i] = ansSize[i];
    }
    return ans;
}

Swift

func partition(_ s: String) -> [[String]] {
    // Convert the string to a character array for accessing and extracting substrings by index
    let s = Array(s)
    // Use double pointer method to check if the substring is a palindrome
    func isPalindrome(start: Int, end: Int) -> Bool {
        var start = start, end = end
        while start < end {
            if s[start] != s[end] { return false }
            start += 1
            end -= 1
        }
        return true
    }

    var result = [[String]]()
    var path = [String]() // Partitioning plan
    func backtracking(startIndex: Int) {
        // Base case, collect results
        guard startIndex < s.count else {
            result.append(path)
            return
        }

        for i in startIndex ..< s.count {
            // Add loop guard, if the current partition is a palindrome substring, then enter backtracking
            guard isPalindrome(start: startIndex, end: i) else { continue }
            path.append(String(s[startIndex ... i]))
            backtracking(startIndex: i + 1) // Find the substring starting at the next starting position
            path = path.dropLast() // Backtracking
        }
    }
    backtracking(startIndex: 0)
    return result
}

Rust

Backtracking + Function to Determine Palindrome Substrings

impl Solution {
    pub fn partition(s: String) -> Vec<Vec<String>> {
        let mut ret = vec![];
        let mut path = vec![];
        let sub_str: Vec<char> = s.chars().collect();
        
        Self::backtracing(&sub_str, 0, &mut ret, &mut path);
        
        ret
    }
    
    fn backtracing(sub_str: &Vec<char>, start: usize, ret: &mut Vec<Vec<String>>, path: &mut Vec<String>) {
        // If the starting position is greater than `s` size, a partitioning solution is found
        if start >= sub_str.len() {
            ret.push(path.clone());
            return;
        }
        
        for i in start..sub_str.len() {
            if !Self::is_palindrome(sub_str, start, i) {
                continue;
            }
            // If it's a palindrome, record it
            let s: String = sub_str[start..i+1].into_iter().collect();
            path.push(s);
            
            // Move the starting position, ensure no repetition
            Self::backtracing(sub_str, i+1, ret, path); 
            path.pop();
        }
    }
    
    fn is_palindrome(s: &Vec<char>, start: usize, end: usize) -> bool {
        let (mut start, mut end) = (start, end);
        
        while start < end {
            if s[start] != s[end] {
                return false;
            }
            
            start += 1;
            end -= 1;
        }

        true
    }
}

Backtracking + Dynamic Programming for Preprocessing Palindrome Substrings

impl Solution {
    pub fn backtracking(is_palindrome: &Vec<Vec<bool>>, result: &mut Vec<Vec<String>>, path: &mut Vec<String>, s: &Vec<char>, start_index: usize) {
        let len = s.len();
        if start_index >= len {
            result.push(path.to_vec());
            return;
        }
        for i in start_index..len {
            if is_palindrome[start_index][i] { path.push(s[start_index..=i].iter().collect::<String>()); } else { continue; }
            Self::backtracking(is_palindrome, result, path, s, i + 1);
            path.pop();
        }
    }

    pub fn partition(s: String) -> Vec<Vec<String>> {
        let mut result: Vec<Vec<String>> = Vec::new();
        let mut path: Vec<String> = Vec::new();
        let s = s.chars().collect::<Vec<char>>();
        let len: usize = s.len();
	// Use dynamic programming to pre-compute
	// A string is a palindrome when (i>j) or length is 1 (i=j) or the first and last characters match and (s[i+1..j−1]) is also a palindrome
        let mut is_palindrome = vec![vec![true; len]; len];
        for i in (0..len).rev() {
            for j in (i + 1)..len {
                is_palindrome[i][j] = s[i] == s[j] && is_palindrome[i + 1][j - 1];
            }
        }
        Self::backtracking(&is_palindrome, &mut result, &mut path, &s, 0);
        result
    }
}

Scala

object Solution {

  import scala.collection.mutable

  def partition(s: String): List[List[String]] = {
    var result = mutable.ListBuffer[List[String]]()
    var path = mutable.ListBuffer[String]()

    // Determine if a string is a palindrome
    def isPalindrome(start: Int, end: Int): Boolean = {
      var (left, right) = (start, end)
      while (left < right) {
        if (s(left) != s(right)) return false
        left += 1
        right -= 1
      }
      true
    }

    // Backtracking algorithm
    def backtracking(startIndex: Int): Unit = {
      if (startIndex >= s.size) {
        result.append(path.toList)
        return
      }
      // Add loop guard, if the current partition is a palindrome substring, enter backtracking
      for (i <- startIndex until s.size if isPalindrome(startIndex, i)) {
        path.append(s.substring(startIndex, i + 1))
        backtracking(i + 1)
        path = path.take(path.size - 1)
      }
    }

    backtracking(0)
    result.toList
  }
}

CSharp

public class Solution
{
    public IList<IList<string>> res = new List<IList<string>>();
    public IList<string> path = new List<string>();
    public IList<IList<string>> Partition(string s)
    {
        BackTracking(s, 0);
        return res;
    }
    public void BackTracking(string s, int start)
    {
        if (start >= s.Length)
        {
            res.Add(new List<string>(path));
            return;
        }

        for (int i = start; i < s.Length; i++)
        {
            if (IsPalindrome(s, start, i))
            {
                path.Add(s.Substring(start, i - start + 1));
            }
            else
            {
                continue;
            }
            BackTracking(s, i + 1);
            path.RemoveAt(path.Count - 1);
        }
    }
    public bool IsPalindrome(string s, int start, int end)
    {
        for (int i = start, j = end; i < j; i++, j--)
        {
            if (s[i] != s[j])
                return false;
        }
        return true;
    }
}