122. Best Time to Buy and Sell Stock II

LeetCode Problem Link (opens new window)

You are given an array where the i-th element represents the price of a given stock on day i.

Design an algorithm to calculate the maximum profit you can achieve. You may complete as many transactions as you like (i.e., buy one and sell one share of the stock multiple times).

Note: You may not engage in multiple transactions at the same time (i.e., you must sell the stock before you buy again).

Example 1:

• Input: [7,1,5,3,6,4]
• Output: 7
• Explanation: Buy on day 2 (price = 1) and sell on day 3 (price = 5), profit = 5-1 = 4. Then buy on day 4 (price = 3) and sell on day 5 (price = 6), profit = 6-3 = 3.

Example 2:

• Input: [1,2,3,4,5]
• Output: 4
• Explanation: Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4. Note that you cannot buy on day 1, buy on day 2 and sell them later, as you are engaging in multiple transactions at the same time. You must sell before buying again.

Example 3:

• Input: [7,6,4,3,1]
• Output: 0
• Explanation: In this case, no transaction is done, i.e., max profit = 0.

Constraints:

• 1 <= prices.length <= 3 * 10^4
• 0 <= prices[i] <= 10^4

Approach

First, understand two key points in this problem:

• There is only one stock!
• Currently, you have the option to either buy or sell the stock.

To earn a profit, at least two days are needed for a transaction.

Greedy Algorithm

This problem might make you initially think about selecting a low price to buy and a high price to sell, then repeat the process for subsequent transactions.

However, if you realize that the final profit can actually be decomposed, the problem becomes much easier!

How can we decompose it?

Suppose you buy on day 0 and sell on day 3, then the profit is prices[3] - prices[0].

This is equivalent to (prices[3] - prices[2]) + (prices[2] - prices[1]) + (prices[1] - prices[0]).

This means breaking down the profit into daily increments rather than considering it as a total from day 0 to day 3!

So, based on prices, you get a series of daily profits: (prices[i] - prices[i - 1]).....(prices[1] - prices[0]).

From the chart:

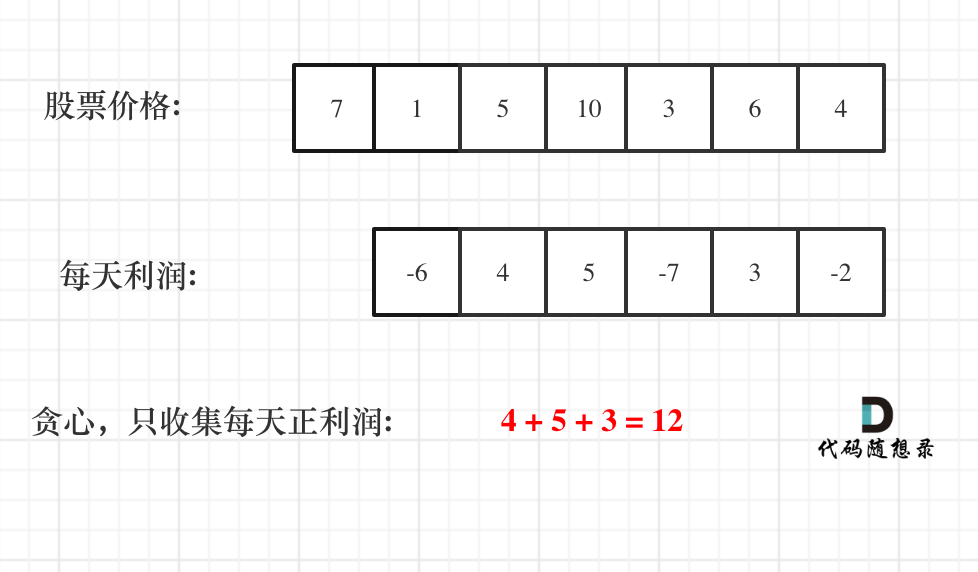
Some people might be confused about the profit on the first day, asking whether it counts or not.

Of course, there is no profit on the first day, and profit can only start accumulating from the second day, hence the profit sequence is one day less than the stock price sequence!

From the chart, you can see that we just need to collect all the positive profits daily, and the intervals where positive profits occur are exactly the intervals where the stock is bought and sold, though we only care about the final profit, not the intervals themselves.

So, only collecting positive profits is what the greedy approach focuses on!

Local optimal: Collect all the positive profits daily, Global optimal: Achieve maximum profit.

Local optimal leads to global optimal, and finding a counterexample proves tough. Try using greedy!

Here is the corresponding C++ code:

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int result = 0;
        for (int i = 1; i < prices.size(); i++) {
            result += max(prices[i] - prices[i - 1], 0);
        }
        return result;
    }
};

• Time complexity: O(n)
• Space complexity: O(1)

Dynamic Programming

Dynamic programming will be detailed in the next series. Here is my C++ code (with detailed comments). If you want to learn it now, you can refer to this: 122. Best Time to Buy and Sell Stock II (Dynamic Programming) (opens new window)

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        // dp[i][1] means maximum cash on day i while holding the stock
        // dp[i][0] means maximum cash on day i without holding any stock
        int n = prices.size();
        vector<vector<int>> dp(n, vector<int>(2, 0));
        dp[0][0] -= prices[0]; // Holding the stock
        for (int i = 1; i < n; i++) {
            // Maximum cash while holding the stock on day i = max(max cash holding stock on day i-1, max cash without holding stock on day i-1 minus buying stock on day i)
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
            // Maximum cash without holding stock on day i = max(max cash without holding stock on day i-1, max cash holding stock on day i-1 plus transaction on day i)
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);
        }
        return max(dp[n - 1][0], dp[n - 1][1]);
    }
};

• Time complexity: $O(n)$
• Space complexity: $O(n)$

Conclusion

The stock problem is indeed part of a series of problems under dynamic programming. Since we are currently discussing the greedy algorithm series, stock problems will be covered in detail later in the dynamic programming series.

As you can see, the greedy algorithm is sometimes cleverer and more efficient than dynamic programming, so don't underestimate the power of the greedy approach.

In this problem, decomposing the profit is the key! Rather than viewing it in a block, break down the total profit into daily profits.

Once you think of it this way, it naturally leads to the greedy approach, which involves collecting all positive profits daily, ensuring a maximum profit in the end.

Other Language Versions

Java:

Greedy:

class Solution {
    public int maxProfit(int[] prices) {
        int result = 0;
        for (int i = 1; i < prices.length; i++) {
            result += Math.max(prices[i] - prices[i - 1], 0);
        }
        return result;
    }
}

Dynamic Programming:

class Solution {
    public int maxProfit(int[] prices) {
        int[][] dp = new int[prices.length][2];

        dp[0][0] = 0;
        dp[0][1] = -prices[0];

        for (int i = 1; i < prices.length; i++) {
            dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
            dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
        }

        return dp[prices.length - 1][0];
    }
}

Python:

Greedy:

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        result = 0
        for i in range(1, len(prices)):
            result += max(prices[i] - prices[i - 1], 0)
        return result

Dynamic Programming:

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        length = len(prices)
        dp = [[0] * 2 for _ in range(length)]
        dp[0][0] = -prices[0]
        dp[0][1] = 0
        for i in range(1, length):
            dp[i][0] = max(dp[i-1][0], dp[i-1][1] - prices[i]) # Note: this is the only difference from 121. Best Time to Buy and Sell Stock
            dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i])
        return dp[-1][1]

Go:

Greedy:

func maxProfit(prices []int) int {
    var sum int
    for i := 1; i < len(prices); i++ {
        if prices[i] - prices[i-1] > 0 {
            sum += prices[i] - prices[i-1]
        }
    }
    return sum
}

Dynamic Programming:

func maxProfit(prices []int) int {
    dp := make([][]int, len(prices))
    for i := 0; i < len(dp); i++ {
        dp[i] = make([]int, 2)
    }
    dp[0][0], dp[0][1] = 0, -prices[0]
    for i := 1; i < len(prices); i++ {
        dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
        dp[i][1] = max(dp[i-1][0] - prices[i], dp[i-1][1])
    }
    return dp[len(prices)-1][0]
}
func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

JavaScript:

Greedy:

var maxProfit = function(prices) {
    let result = 0;
    for(let i = 1; i < prices.length; i++) {
        result += Math.max(prices[i] - prices[i - 1], 0);
    }
    return result;
};

Dynamic Programming:

const maxProfit = (prices) => {
  let dp = Array.from(Array(prices.length), () => Array(2).fill(0));
  dp[0][0] = 0 - prices[0];
  dp[0][1] = 0;
  for (let i = 1; i < prices.length; i++) {
    dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
    dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] + prices[i]);
  }

  return dp[prices.length - 1][1];
};

TypeScript:

Greedy:

function maxProfit(prices: number[]): number {
  let resProfit: number = 0;
  for (let i = 1, length = prices.length; i < length; i++) {
    resProfit += Math.max(prices[i] - prices[i - 1], 0);
  }
  return resProfit;
}

Dynamic Programming:

function maxProfit(prices: number[]): number {
  const dp = Array(prices.length)
    .fill(0)
    .map(() => Array(2).fill(0));
  dp[0][0] = -prices[0];
  for (let i = 1; i < prices.length; i++) {
    dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
    dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] + prices[i]);
  }
  return dp[prices.length - 1][1];
}

Rust:

Greedy:

impl Solution {
    pub fn max_profit(prices: Vec<i32>) -> i32 {
        let mut result = 0;
        for i in 1..prices.len() {
            result += (prices[i] - prices[i - 1]).max(0);
        }
        result
    }
}

Dynamic Programming:

impl Solution {
    pub fn max_profit(prices: Vec<i32>) -> i32 {
        let mut dp = vec![vec![0; 2]; prices.len()];
        dp[0][0] = -prices[0];
        for i in 1..prices.len() {
            dp[i][0] = dp[i - 1][0].max(dp[i - 1][1] - prices[i]);
            dp[i][1] = dp[i - 1][1].max(dp[i - 1][0] + prices[i]);
        }
        dp[prices.len() - 1][1]
    }
}

C:

Greedy:

int maxProfit(int* prices, int pricesSize){
    int result = 0;
    int i;
    for(i = 1; i < pricesSize; ++i) {
        if(prices[i] > prices[i-1])
            result+= prices[i]-prices[i-1];
    }
    return result;
}

Dynamic Programming:

#define max(a, b) (((a) > (b)) ? (a) : (b))

int maxProfit(int* prices, int pricesSize){
    int dp[pricesSize][2];
    dp[0][0] = 0 - prices[0];
    dp[0][1] = 0;

    int i;
    for(i = 1; i < pricesSize; ++i) {
        dp[i][0] = max(dp[i-1][0], dp[i-1][1] - prices[i]);
        dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i]);
    }
    return dp[pricesSize - 1][1];
}

Scala:

Greedy:

object Solution {
  def maxProfit(prices: Array[Int]): Int = {
    var result = 0
    for (i <- 1 until prices.length) {
      if (prices(i) > prices(i - 1)) {
        result += prices(i) - prices(i - 1)
      }
    }
    result
  }
}

C#

public class Solution
{
    public int MaxProfit(int[] prices)
    {
        int res = 0;
        for (int i = 0; i < prices.Length - 1; i++)
        {
            res += Math.Max(0, prices[i + 1] - prices[i]);
        }
        return res;
    }
}