700. Search in a Binary Search Tree

LeetCode Problem Address (opens new window)

Given the root node of a binary search tree (BST) and a value. You need to find the node in the BST where the node's value equals the given value. Return the subtree rooted with that node. If such node doesn't exist, return NULL.

For example,

In the above example, if the value we want to find is 5, since there is no node with value 5, we should return NULL.

Thought Process

Previously, we have dealt with ordinary binary trees, now let's take a look at binary search trees.

In Binary Tree Basics (opens new window), we have already discussed binary search trees.

A binary search tree is a tree with order:

• If its left subtree is not empty, then all the nodes in the left subtree have values less than the root node's value.
• If its right subtree is not empty, then all the nodes in the right subtree have values greater than the root node's value.
• Both the left and right subtrees must also be binary search trees.

This means that recursion and iterative traversal for a BST differ from those for ordinary binary trees.

This problem is about searching for a node in a BST. So let's see how we can traverse it.

Recursive Approach

1. Determine the Parameters and Return Value of the Recursive Function

The parameters for the recursive function are the root node and the value to be searched, and it returns the node where the value is found.

Here is the code:

TreeNode* searchBST(TreeNode* root, int val)

2. Set the Termination Condition

If the root is NULL, or if the root's value equals the value being searched, return the root node.

if (root == NULL || root->val == val) return root;

3. Set the Logic of a Single Layer of Recursion

Let's see how the recursion logic for a BST is different.

Because a BST is ordered, we can search in a directed manner.

If root->val > val, search the left subtree. If root->val < val, search the right subtree. If the value is not found, return NULL.

Here is the code:

TreeNode* result = NULL;
if (root->val > val) result = searchBST(root->left, val);
if (root->val < val) result = searchBST(root->right, val);
return result;

Many users write recursive functions like searchBST(root->left, val) without considering that the recursive function also has a return value.

What is the return value of the recursive function? If the left subtree finds the value, the node must be returned. If you don't use a variable to capture it, the return value is lost.

So it should be result = searchBST(root->left, val).

Overall code is as follows:

class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        if (root == NULL || root->val == val) return root;
        TreeNode* result = NULL;
        if (root->val > val) result = searchBST(root->left, val);
        if (root->val < val) result = searchBST(root->right, val);
        return result;
    }
};

Or we can write it like this:

class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        if (root == NULL || root->val == val) return root;
        if (root->val > val) return searchBST(root->left, val);
        if (root->val < val) return searchBST(root->right, val);
        return NULL;
    }
};

Iterative Approach

When it comes to iterative traversal for binary trees, you might immediately think of using a stack for depth-first traversal, or using a queue for breadth-first traversal.

For binary search trees, it's different. Due to the special property of BSTs, we can write iterative traversal without auxiliary stacks or queues.

For an ordinary binary tree, there's backtracking during recursion, such as when reaching the end of a left path and needing to backtrack before moving to the right path.

For a binary search tree, there's no need for backtracking because the orderliness of the nodes dictates the search direction.

For instance, if you want to search for a node with a value of 3, there's no need to search other nodes or backtrack. The search path is predefined.

If the current node is greater than 3, move left. If less than 3, move right, as shown below:

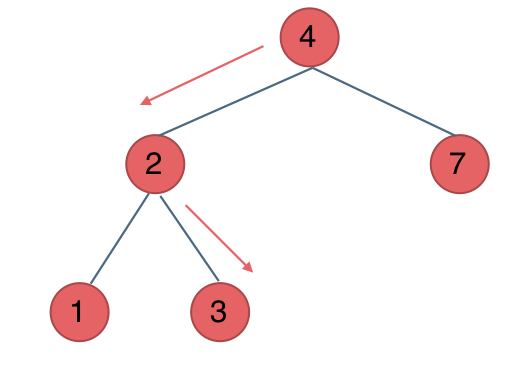
Thus, the iterative code is as follows:

class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        while (root != NULL) {
            if (root->val > val) root = root->left;
            else if (root->val < val) root = root->right;
            else return root;
        }
        return NULL;
    }
};

Seeing such a simple iterative method for the first time might bring tears of joy! Have a little cry~

Summary

In this document, we introduced traversal methods for binary search trees. Because of the orderliness, traversals are much simpler than for ordinary binary trees.

However, some people tend to overlook the properties of binary search trees, resulting in unnecessarily complicated traversal code.

Thus, when working on problems involving binary search trees, remember to utilize their properties.

I've provided both recursive and iterative methods here. The simplicity of the code is evident, leveraging the orderliness inherent to BSTs.

Other Language Versions

Java

class Solution {
    // Recursive, ordinary binary tree
    public TreeNode searchBST(TreeNode root, int val) {
        if (root == null || root.val == val) {
            return root;
        }
        TreeNode left = searchBST(root.left, val);
        if (left != null) {
            return left;
        }
        return searchBST(root.right, val);
    }
}

class Solution {
    // Recursive, optimized using BST characteristics
    public TreeNode searchBST(TreeNode root, int val) {
        if (root == null || root.val == val) {
            return root;
        }
        if (val < root.val) {
            return searchBST(root.left, val);
        } else {
            return searchBST(root.right, val);
        }
    }
}

class Solution {
    // Iterative, ordinary binary tree
    public TreeNode searchBST(TreeNode root, int val) {
        if (root == null || root.val == val) {
            return root;
        }
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()) {
            TreeNode pop = stack.pop();
            if (pop.val == val) {
                return pop;
            }
            if (pop.right != null) {
                stack.push(pop.right);
            }
            if (pop.left != null) {
                stack.push(pop.left);
            }
        }
        return null;
    }
}

class Solution {
    // Iterative, optimized using BST characteristics, no stack needed
    public TreeNode searchBST(TreeNode root, int val) {
        while (root != null)
            if (val < root.val) root = root.left;
            else if (val > root.val) root = root.right;
            else return root;
        return null;
    }
}

Python

(Approach 1) Recursive

class Solution:
    def searchBST(self, root: TreeNode, val: int) -> TreeNode:
        # Why is there a return value: 
        # Because once the target node is found, it should be returned immediately,
        # This ensures finding the node and returning just the part of the tree we are searching, avoiding full tree traversal.

        if not root or root.val == val: 
            return root

        if root.val > val: 
            return self.searchBST(root.left, val)

        if root.val < val: 
            return self.searchBST(root.right, val)

(Approach 2) Iterative

class Solution:
    def searchBST(self, root: TreeNode, val: int) -> TreeNode:
        while root:
            if val < root.val: root = root.left
            elif val > root.val: root = root.right
            else: return root
        return None

(Approach 3) Stack-based Traversal

class Solution:
    def searchBST(self, root: TreeNode, val: int) -> TreeNode:
        stack = [root]
        while stack:
            node = stack.pop()
            # Based on TreeNode definition
            # Node carries three types of information: node.left / node.right / node.val
            # If val is found, return node, indicating the subtree rooted with the found node
            # Order of node.left / node.right / val can be interchanged
            if node.val == val: 
                return node
            if node.right:
                stack.append(node.right)
            if node.left:
                stack.append(node.left)
        return None

Go

Recursive Approach:

// Recursive Approach
func searchBST(root *TreeNode, val int) *TreeNode {
    if root == nil || root.Val == val {
        return root
    }
    if root.Val > val {
        return searchBST(root.Left, val)
    }
    return searchBST(root.Right, val)
}

Iterative Approach:

// Iterative Approach
func searchBST(root *TreeNode, val int) *TreeNode {
    for root != nil {
        if root.Val > val {
            root = root.Left
        } else if root.Val < val {
            root = root.Right
        } else {
            return root
        }
    }
    return nil
}

JavaScript

Recursive:

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} val
 * @return {TreeNode}
 */
var searchBST = function (root, val) {
    if (!root || root.val === val) {
        return root;
    }
    if (root.val > val)
        return searchBST(root.left, val);
    if (root.val < val)
        return searchBST(root.right, val);
};

Iterative:

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} val
 * @return {TreeNode}
 */
var searchBST = function (root, val) {
    while (root !== null) {
        if (root.val > val)
            root = root.left;
        else if (root.val < val)
            root = root.right;
        else 
            return root;
    }
    return null;
};

TypeScript

Recursive Approach

function searchBST(root: TreeNode | null, val: number): TreeNode | null {
    if (root === null || root.val === val) return root;
    if (root.val < val) return searchBST(root.right, val);
    if (root.val > val) return searchBST(root.left, val);
    return null;
};

Iterative Approach

function searchBST(root: TreeNode | null, val: number): TreeNode | null {
    let resNode: TreeNode | null = root;
    while (resNode !== null) {
        if (resNode.val === val) return resNode;
        if (resNode.val < val) {
            resNode = resNode.right;
        } else {
            resNode = resNode.left;
        }
    }
    return null;
};

Scala

Recursive:

object Solution {
  def searchBST(root: TreeNode, value: Int): TreeNode = {
    if (root == null || value == root.value) return root
    // Similar to ternary operations, in Scala, if...else has a return value
    if (value < root.value) searchBST(root.left, value) else searchBST(root.right, value)
  }
}

Iterative:

object Solution {
  def searchBST(root: TreeNode, value: Int): TreeNode = {
    // Since root is immutable, it needs to be assigned to a mutable variable
    var node = root
    while (node != null) {
      if (value < node.value) node = node.left
      else if (value > node.value) node = node.right
      else return node
    }
    null // Return null if no value is found
  }
}

Rust

Recursive:

use std::cell::RefCell;
use std::rc::Rc;
impl Solution {
    pub fn search_bst(
        root: Option<Rc<RefCell<TreeNode>>>,
        val: i32,
    ) -> Option<Rc<RefCell<TreeNode>>> {
        if root.is_none() || root.as_ref().unwrap().borrow().val == val {
            return root;
        }
        let node_val = root.as_ref().unwrap().borrow().val;
        if node_val > val {
            return Self::search_bst(root.as_ref().unwrap().borrow().left.clone(), val);
        }
        if node_val < val {
            return Self::search_bst(root.unwrap().borrow().right.clone(), val);
        }
        None
    }
}

Iterative:

use std::cell::RefCell;
use std::rc::Rc;
use std::cmp;
impl Solution {
    pub fn search_bst(
        mut root: Option<Rc<RefCell<TreeNode>>>,
        val: i32,
    ) -> Option<Rc<RefCell<TreeNode>>> {
        while let Some(ref node) = root.clone() {
            match val.cmp(&node.borrow().val) {
                cmp::Ordering::Less => root = node.borrow().left.clone(),
                cmp::Ordering::Equal => return root,
                cmp::Ordering::Greater => root = node.borrow().right.clone(),
            };
        }
        None
    }
}

C#

// Recursive
public TreeNode SearchBST(TreeNode root, int val)
{
    if (root == null || root.val == val) return root;
    if (root.val > val) return SearchBST(root.left, val);
    if (root.val < val) return SearchBST(root.right, val);
    return null;
}
//  Iterative
public TreeNode SearchBST(TreeNode root, int val)
{
    while (root != null)
    {
        if (root.val > val) root = root.left;
        else if (root.val < val) root = root.right;
        else return root;
    }
    return null;
}