Binary Tree: Summary Edition! (All the Binary Tree Skills You Need to Master Are Here)

LeetCode Binary Tree Big Summary!

Unknowingly, the binary tree has been with us for thirty-three days, “Code Thinking Record” (opens new window) has published thirty-three articles on binary trees, providing detailed explanations on 30+ classic binary tree problems. Those who have persisted must have a deep understanding of binary trees.

In each binary tree problem, I have used the three-step method of recursion to analyze the problem. I believe that whenever you see a binary tree, or recursion, you'll think: what are the return values and parameters? What is the termination condition? What is the single-layer logic?

Moreover, I have provided the corresponding iterative method for almost every problem, which can further improve your skills.

Below, Carl categorizes the analyzed problems, which can help new learners to learn binary trees step-by-step, and allow experienced learners to quickly review before interviews. See a title and recall the problem-solving approach; this way, you'll be able to systematically review the binary tree topic quickly.

The posting order of the articles on the public account is gradual, so the categories below roughly follow the article's posting order. I further provide a systematic classification.

Basic Theory of Binary Trees

• Binary Tree Basics (opens new window): Types of binary trees, storage methods, traversal methods, definition methods

Traversal Methods of Binary Trees

• Depth-First Traversal
  • Binary Tree Recursive Traversal (opens new window): Recursion three-step method first shown
  • Binary Tree Iterative Traversal (opens new window): Simulating recursion with a stack
  • Unified Iterative Traversal of Binary Tree (opens new window)
• Breadth-First Traversal
  • 0102.Binary Tree Level Order Traversal (opens new window): Simulating with a queue

Calculate Properties of a Binary Tree

• 0101.Symmetric Tree (opens new window)
  • Recursion: Postorder, compare whether the left and right subtrees of the root node are mirror images of each other
  • Iteration: Use a queue/stack to sequentially put two nodes into the container for comparison
• 0104.Maximum Depth of Binary Tree (opens new window)
  • Recursion: Postorder, the maximum height of the root node is the maximum depth, calculate tree height through the return value of the recursion function
  • Iteration: Level-order traversal
• 0111.Minimum Depth of Binary Tree (opens new window)
  • Recursion: Postorder, the minimum height of the root node is the minimum depth; pay attention to the definition of minimum depth
  • Iteration: Level-order traversal
• 0222.Count Complete Tree Nodes (opens new window)
  • Recursion: Postorder, calculate the number of nodes through the return value of the recursion function
  • Iteration: Level-order traversal
• 0110.Balanced Binary Tree (opens new window)
  • Recursion: Postorder, note the difference between postorder for height and pre-order for depth, and the recursion process checks the height difference
  • Iteration: Very inefficient, not recommended
• 0257.Binary Tree Paths (opens new window)
  • Recursion: Preorder, easily lets the parent node point to the child nodes, involves backtracking handling root-to-leaf paths
  • Iteration: One stack simulates recursion, one stack for storing the corresponding traversal path
• Binary Tree Traversal with Recursion and Backtracking (opens new window)
  • Detailed explanation of how recursion hides backtracking in 0257.Binary Tree Paths (opens new window)
• 0404.Sum of Left Leaves (opens new window)
  • Recursion: Postorder, three-layer constraint condition needed to determine if it is a left leaf.
  • Iteration: Direct simulation of postorder traversal
• 0513.Find Bottom Left Tree Value (opens new window)
  • Recursion: Order doesn't matter, prioritize searching the left child while finding the deepest leaf node.
  • Iteration: Level-order traversal finds the leftmost node of the last row
• 0112.Path Sum (opens new window)
  • Recursion: Order doesn't matter, the recursion function's return value is bool for searching a single path, no return value for searching the whole tree.
  • Iteration: Stack elements record both node pointers and the path total sum from the head node to that node

Modify and Construct Binary Trees

• 0226.Invert Binary Tree (opens new window)
  • Recursion: Preorder, swap left and right children
  • Iteration: Directly simulate preorder traversal
• 0106.Construct Binary Tree from Inorder and Postorder Traversal (opens new window)
  • Recursion: Preorder, the key is to find the partition point and construct the left and right intervals
  • Iteration: Quite complex, not very meaningful
• 0654.Maximum Binary Tree (opens new window)
  • Recursion: Preorder, partition point is the maximum value of the array, construct the left and right intervals
  • Iteration: Quite complex, not very meaningful
• 0617.Merge Two Binary Trees (opens new window)
  • Recursion: Preorder, operate on nodes of two trees simultaneously, pay attention to the rules of merging
  • Iteration: Use a queue, similar to level-order traversal

Calculate Properties of a Binary Search Tree

• 0700.Search in a Binary Search Tree (opens new window)
  • Recursion: The recursion of a binary search tree is directional
  • Iteration: Because it has a direction, the iterative method is straightforward
• 0098.Validate Binary Search Tree (opens new window)
  • Recursion: Inorder, equivalent to checking if a sequence is increasing
  • Iteration: Simulate inorder, logic is the same
• 0530.Minimum Absolute Difference in BST (opens new window)
  • Recursion: Inorder, dual-pointer operation
  • Iteration: Simulate inorder, logic is the same
• 0501.Find Mode in Binary Search Tree (opens new window)
  • Recursion: Inorder, trick to clear result set, can obtain mode collection with one traversal
• 0538.Convert BST to Greater Tree (opens new window)
  • Recursion: Inorder, dual-pointer operation accumulation
  • Iteration: Simulate inorder, logic is the same

Common Ancestor Problems in Binary Trees

• 0236.Lowest Common Ancestor of a Binary Tree (opens new window)
  • Recursion: Postorder, backtrack to find nodes where target values appear in the left and right subtrees.
  • Iteration: Not suitable for simulating backtracking
• 0235.Lowest Common Ancestor of a Binary Search Tree (opens new window)
  • Recursion: Order doesn't matter; if the node's value is within the target range, it is the nearest common ancestor.
  • Iteration: Inorder traversal

Modifying and Constructing Binary Search Trees

• 0701.Insert into a Binary Search Tree (opens new window)
  • Recursion: Order doesn't matter; insert node via the return value of the recursive function
  • Iteration: Sequential traversal, need to record the parent node to perform the insertion
• 0450.Delete Node in a BST (opens new window)
  • Recursion: Preorder, think clearly about the situation of deleting non-leaf nodes
  • Iteration: Ordered traversal, quite complex
• 0669.Trim a Binary Search Tree (opens new window)
  • Recursion: Preorder, remove nodes via the return value of the recursive function
  • Iteration: Ordered traversal, quite complex
• 0108.Convert Sorted Array to Binary Search Tree (opens new window)
  • Recursion: Preorder, middle node of the array partitions
  • Iteration: Quite complex, simulate with three queues

Phase Summary

After completing the above problems, be sure to see the following phase summaries:

Weekly summaries will provide unified answers to everyone's questions and supplement the week's content, so be sure to review them, which will help you capture all scattered knowledge points!

• Weekly Summary! (Binary Tree Series 1) (opens new window)
• Weekly Summary! (Binary Tree Series 2) (opens new window)
• Weekly Summary! (Binary Tree Series 3) (opens new window)
• Weekly Summary! (Binary Tree Series 4) (opens new window)

Final Summary

Many students have difficulty choosing a traversal order for binary tree problems. We've done so many binary tree problems; Carl gives a general classification for everyone here.

• If it involves the construction of a binary tree, whether a regular binary tree or a binary search tree, always use preorder, as the middle node is constructed first.

• To determine the properties of a regular binary tree, it is typically postorder, as the return values of the recursive function are often used for calculations.

• To find properties of a binary search tree, it must be inorder, or else its ordering nature is wasted.

Note that in determining the properties of a regular binary tree, I use "typically" for postorder. For instance, achieving depth can also use preorder, and 0257.Binary Tree Paths (opens new window) also used preorder for the parent node to easily point to child nodes.

So, for determining the properties of a regular binary tree, it still requires specific analysis of the specific problem.

Binary Tree Special Topic Gathered into One Chart:

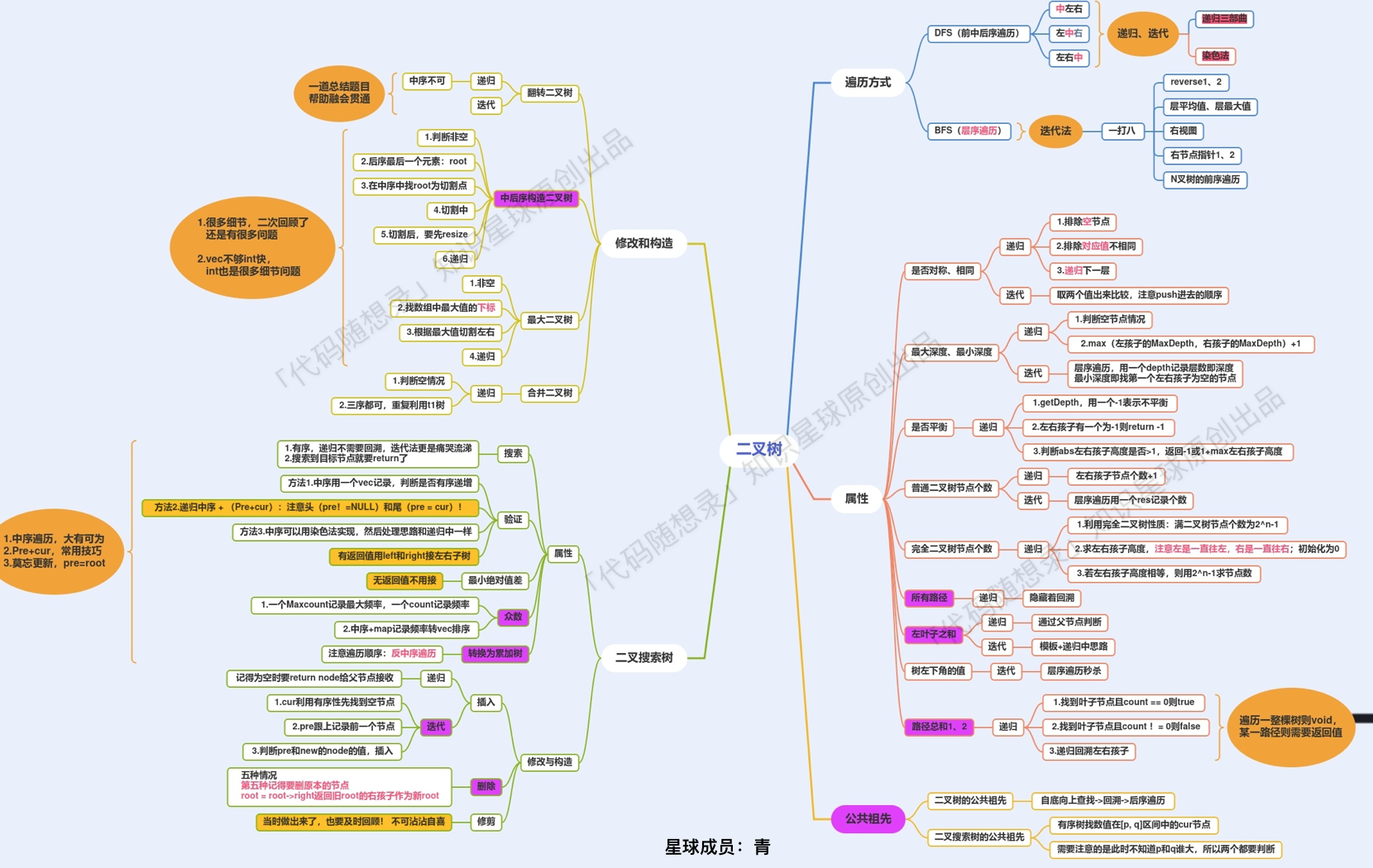
This chart is created by a code thought blog knowledge planet (opens new window) member: Qing (opens new window). It summarizes the content quite well, and it's shared with everyone here.

Finally, the binary tree series is perfectly concluded, and it seems this should be the longest series. Thanks for everyone's 33 days of persistence and companionship. We’re going to start a new series, "Backtracking Algorithm"!