# 112. Path Sum
LeetCode problem link (opens new window)
Given a binary tree and a target sum, determine if the tree has a root-to-leaf path such that adding up all the values along the path equals the target sum.
Note: A leaf is a node with no children.
Example: Given the following binary tree, and sum = 22,
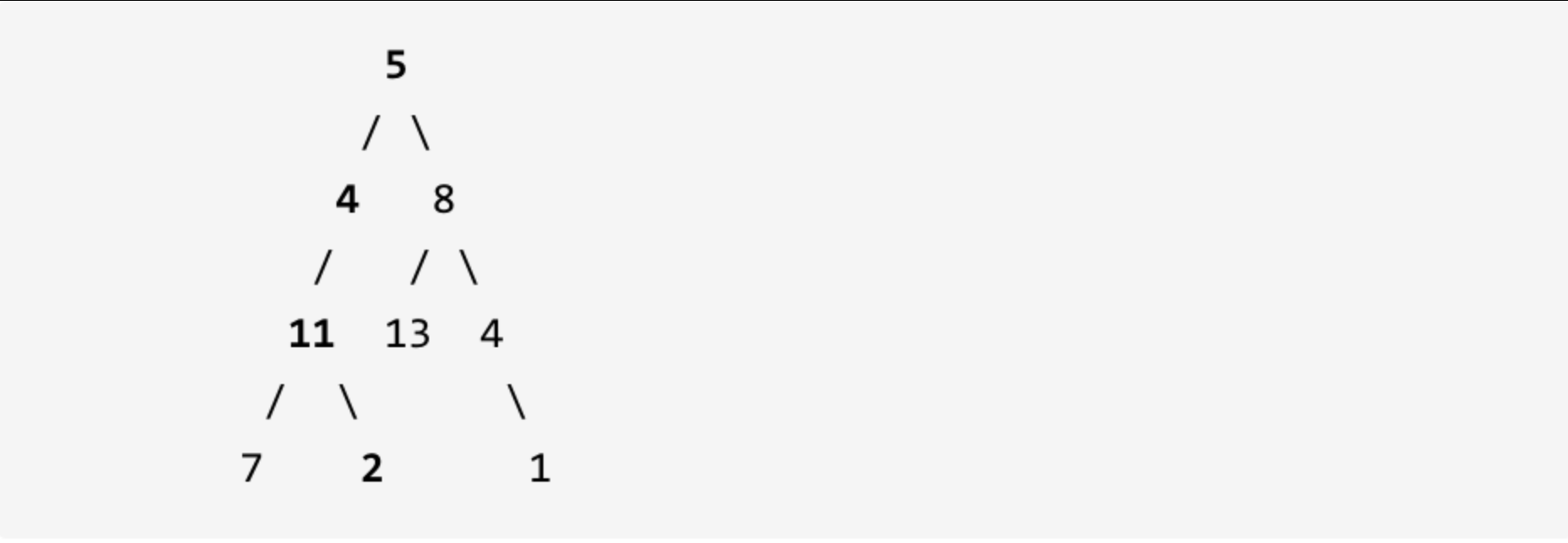
Return true, as there exists a root-to-leaf path 5->4->11->2 which equals the target sum 22.
# Solution
I believe many of you are wondering when a recursive function needs a return value and when it doesn't, especially when the return type of the recursive function is bool.
I will explain this through a detailed discussion of the following two problems:
In this problem, we want to traverse paths from the root to leaflet nodes and check if the path sum equals the target sum.
# Recursion
We can use a depth-first search approach (preorder, inorder, and postorder all work for this problem as the middle node doesn't have any specific logic) to traverse the binary tree.
- Determine the parameters and return type of the recursive function
Parameters: We need the root of the binary tree and an accumulator to track whether the sum of a path equals the target sum. The accumulator should be of type int.
Regarding return type, when does a recursive function need a return type? When doesn't it? Here are three points to summarize:
- If you need to traverse the entire binary tree without processing the return value of the recursion, the recursive function should not have a return value. (This is the case in Part 2 of this text, in 113. Path Sum II (opens new window))
- If you need to traverse the entire binary tree and handle the return value of recursion, the recursive function needs a return value. (This is discussed in the solution for 0236. Lowest Common Ancestor of a Binary Tree (opens new window))
- If you need to find one path that meets the condition, the recursive function must have a return value, because as soon as you find one, you should return immediately. (This is the case in this problem)
In this problem, we need to find one path that meets the condition, so the recursive function should have a boolean return type to promptly return when we find a valid path.
So the code can be like:
bool traversal(TreeNode* cur, int count) // Note the return type of the function
- Determine the termination condition
How do we calculate the path sum using the accumulator?
Rather than gathering and comparing with the target sum, we can decrement the accumulator, starting it with the target sum, and subtract the values of the path nodes as we traverse.
If count == 0 and we've reached a leaf node, we found the target sum. If not, and we've reached a leaf node, it means we didn't find the path.
The recursive termination conditions can be coded as follows:
if (!cur->left && !cur->right && count == 0) return true; // reach a leaf node and the count is zero
if (!cur->left && !cur->right) return false; // reached a leaf node without finding a valid path
2
- Determine the logic within one level of recursion
Because the termination condition considers leaf nodes, we shouldn't let null nodes enter the recursion process.
The recursive function returns a value, and if it returns true, it means a valid path was found and should return immediately.
The code can be illustrated as:
if (cur->left) { // Traverse the left (ignoring null nodes)
// Immediately return true if a leaf node returns true
if (traversal(cur->left, count - cur->left->val)) return true; // Note the backtracking logic
}
if (cur->right) { // Traverse the right (ignoring null nodes)
// Immediately return true if a leaf node returns true
if (traversal(cur->right, count - cur->right->val)) return true; // Note the backtracking logic
}
return false;
2
3
4
5
6
7
8
9
In the above code, backtracking logic is embedded. Without backtracking, we can't look for other paths.
Backtracking is hidden in traversal(cur->left, count - cur->left->val). Because count - cur->left->val is passed as the parameter directly, the count value remains unchanged when the function ends.
To explicitly show the backtracking process, the code can be enhanced like:
if (cur->left) { // Left
count -= cur->left->val; // recursive, process the node
if (traversal(cur->left, count)) return true;
count += cur->left->val; // backtrack, undo the processed result
}
if (cur->right) { // Right
count -= cur->right->val;
if (traversal(cur->right, count)) return true;
count += cur->right->val;
}
return false;
2
3
4
5
6
7
8
9
10
11
The complete code is as follows:
class Solution {
private:
bool traversal(TreeNode* cur, int count) {
if (!cur->left && !cur->right && count == 0) return true; // reach a leaf node and the count is zero
if (!cur->left && !cur->right) return false; // reached a leaf node without finding a valid path
if (cur->left) { // Left
count -= cur->left->val; // recursive, process the node
if (traversal(cur->left, count)) return true;
count += cur->left->val; // backtrack, undo the processed result
}
if (cur->right) { // Right
count -= cur->right->val; // recursive, process the node
if (traversal(cur->right, count)) return true;
count += cur->right->val; // backtrack, undo the processed result
}
return false;
}
public:
bool hasPathSum(TreeNode* root, int sum) {
if (root == NULL) return false;
return traversal(root, sum - root->val);
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
After refining, the code becomes:
class Solution {
public:
bool hasPathSum(TreeNode* root, int sum) {
if (!root) return false;
if (!root->left && !root->right && sum == root->val) {
return true;
}
return hasPathSum(root->left, sum - root->val) || hasPathSum(root->right, sum - root->val);
}
};
2
3
4
5
6
7
8
9
10
Realize that once the code is refined, the detailed analysis process might not be visible. Ensure to understand the problem clearly before proceeding with code refinement! This is a point I emphasized many times!
# Iteration
If using a stack to simulate recursion, how to backtrack?
At this point, an element in the stack must record not only the pointer to the node but also the sum of the path from the root node to that node.
In C++, we can use a pair structure to store the elements in the stack.
Define it as pair<TreeNode*, int> - a pair of a node pointer and the path sum.
The following code simulates preorder traversal using a stack (detailed comments included):
class Solution {
public:
bool hasPathSum(TreeNode* root, int sum) {
if (root == NULL) return false;
// At this point, the stack must have elements of type pair<Node pointer, Path value>
stack<pair<TreeNode*, int>> st;
st.push(pair<TreeNode*, int>(root, root->val));
while (!st.empty()) {
pair<TreeNode*, int> node = st.top();
st.pop();
// If the current node is a leaf and the path sum equals sum, return true
if (!node.first->left && !node.first->right && sum == node.second) return true;
// Right node: when pushing a node, also record the path sum to the node
if (node.first->right) {
st.push(pair<TreeNode*, int>(node.first->right, node.second + node.first->right->val));
}
// Left node: when pushing a node, also record the path sum to the node
if (node.first->left) {
st.push(pair<TreeNode*, int>(node.first->left, node.second + node.first->left->val));
}
}
return false;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
Once you thoroughly understand the recursive method for this problem, you can also address 113. Path Sum II (opens new window).
# Related Problem Recommendation
# 113. Path Sum II
LeetCode problem link (opens new window)
Given a binary tree and a sum, find all root-to-leaf paths where each path's sum equals the given sum.
Note: A leaf is a node with no children.
Example: Given the following binary tree and sum = 22,
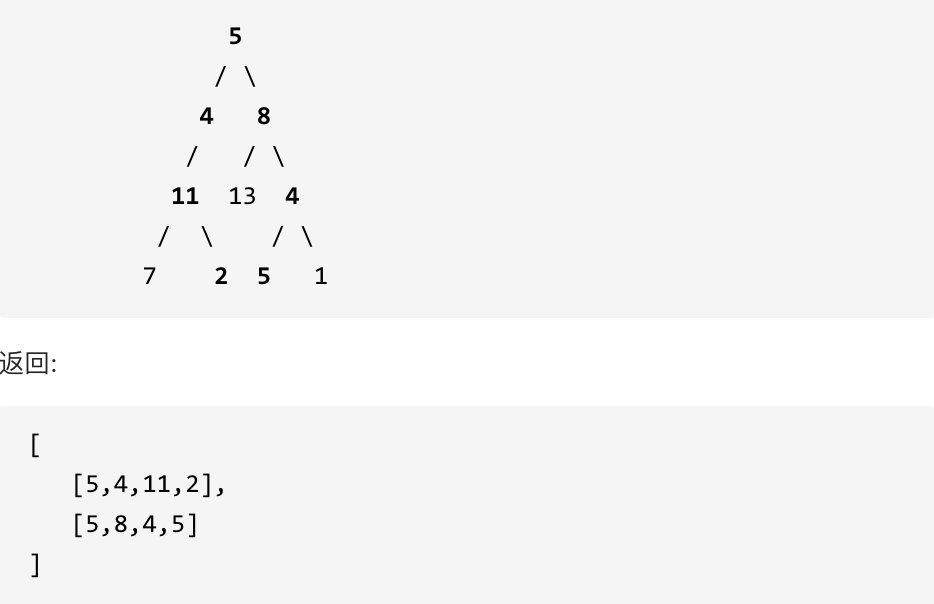
# Solution
- Path Sum II needs to traverse the entire tree to find all paths, so the recursive function should not have a return value!
As shown in the diagram:
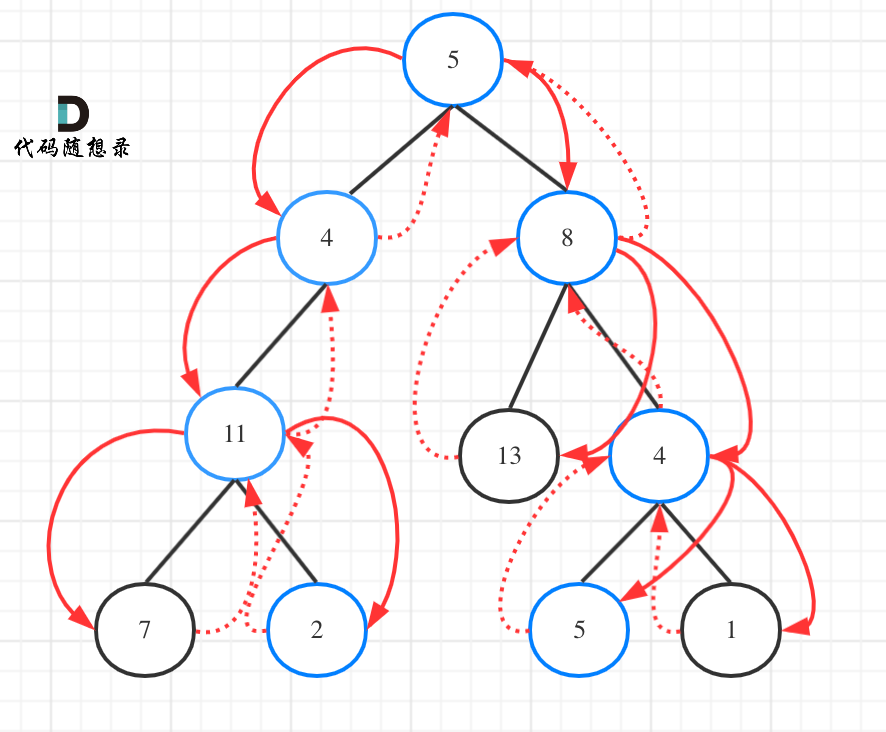
To illustrate the steps as clearly as possible, here is a code snippet that is not necessarily concise but very clear in logic:
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
// The recursive function does not need to return a value because we need to traverse the entire tree
void traversal(TreeNode* cur, int count) {
if (!cur->left && !cur->right && count == 0) { // reach leaf and a path sum found
result.push_back(path);
return;
}
if (!cur->left && !cur->right) return; // reach leaf with path sum not found
if (cur->left) { // Left (ignore null nodes)
path.push_back(cur->left->val);
count -= cur->left->val;
traversal(cur->left, count); // recursion
count += cur->left->val; // backtracking
path.pop_back(); // backtracking
}
if (cur->right) { // Right (ignore null nodes)
path.push_back(cur->right->val);
count -= cur->right->val;
traversal(cur->right, count); // recursion
count += cur->right->val; // backtracking
path.pop_back(); // backtracking
}
return;
}
public:
vector<vector<int>> pathSum(TreeNode* root, int sum) {
result.clear();
path.clear();
if (root == NULL) return result;
path.push_back(root->val); // Add root to path
traversal(root, sum - root->val);
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
As for the iterative method for 113. Path Sum II (opens new window) I've not included it, as it becomes more cumbersome using iteration for tracking all paths, and it's unnecessary if you fully grasp the recursive method. If you are interested, you could further research this.
# Summary
Through the detailed explanation of 112. Path Sum (opens new window) and 113. Path Sum II (opens new window), we addressed when a recursive function needs a return value and when it doesn't.
These two problems are excellent for mastering this knowledge point. After reading the explanation here and trying the problems, you will better understand the difference between searching an entire tree and finding a specific path.
For 112. Path Sum (opens new window), I provided both recursive and iterative methods, though the iterative approach adds complexity. Mastering the recursive way should suffice!
# Other Language Versions
# Java
- Path Sum
class Solution {
public boolean hasPathSum(TreeNode root, int targetSum) {
if (root == null) {
return false;
}
targetSum -= root.val;
// Leaf node
if (root.left == null && root.right == null) {
return targetSum == 0;
}
if (root.left != null) {
boolean left = hasPathSum(root.left, targetSum);
if (left) { // already found, return early
return true;
}
}
if (root.right != null) {
boolean right = hasPathSum(root.right, targetSum);
if (right) { // already found, return early
return true;
}
}
return false;
}
}
// lc112 concise method
class Solution {
public boolean hasPathSum(TreeNode root, int targetSum) {
if (root == null) return false; // exit if null
// Leaf node check if meets
if (root.left == null && root.right == null) return root.val == targetSum;
// Sums on both sides of the branch
return hasPathSum(root.left, targetSum - root.val) || hasPathSum(root.right, targetSum - root.val);
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
Iteration
class Solution {
public boolean hasPathSum(TreeNode root, int targetSum) {
if(root == null) return false;
Stack<TreeNode> stack1 = new Stack<>();
Stack<Integer> stack2 = new Stack<>();
stack1.push(root);
stack2.push(root.val);
while(!stack1.isEmpty()) {
int size = stack1.size();
for(int i = 0; i < size; i++) {
TreeNode node = stack1.pop();
int sum = stack2.pop();
// If this node is a leaf and the path sum equals targetSum, return true
if(node.left == null && node.right == null && sum == targetSum) {
return true;
}
// Right node, push a node while also recording the path sum
if(node.right != null){
stack1.push(node.right);
stack2.push(sum + node.right.val);
}
// Left node, push a node while also recording the path sum
if(node.left != null) {
stack1.push(node.left);
stack2.push(sum + node.left.val);
}
}
}
return false;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public boolean hasPathSum(TreeNode root, int targetSum) {
Stack<TreeNode> treeNodeStack = new Stack<>();
Stack<Integer> sumStack = new Stack<>();
if(root == null)
return false;
treeNodeStack.add(root);
sumStack.add(root.val);
while(!treeNodeStack.isEmpty()){
TreeNode curr = treeNodeStack.peek();
int tempsum = sumStack.pop();
if(curr != null){
treeNodeStack.pop();
treeNodeStack.add(curr);
treeNodeStack.add(null);
sumStack.add(tempsum);
if(curr.right != null){
treeNodeStack.add(curr.right);
sumStack.add(tempsum + curr.right.val);
}
if(curr.left != null){
treeNodeStack.add(curr.left);
sumStack.add(tempsum + curr.left.val);
}
}else{
treeNodeStack.pop();
TreeNode temp = treeNodeStack.pop();
if(temp.left == null && temp.right == null && tempsum == targetSum)
return true;
}
}
return false;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
- Path Sum II
class Solution {
public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
List<List<Integer>> res = new ArrayList<>();
if (root == null) return res; // non-null check
List<Integer> path = new LinkedList<>();
preOrderDfs(root, targetSum, res, path);
return res;
}
public void preOrderDfs(TreeNode root, int targetSum, List<List<Integer>> res, List<Integer> path) {
path.add(root.val);
// Reached a leaf node
if (root.left == null && root.right == null) {
// Found a path with targetSum
if (targetSum - root.val == 0) {
res.add(new ArrayList<>(path));
}
return; // if sum not equal, return
}
if (root.left != null) {
preOrderDfs(root.left, targetSum - root.val, res, path);
path.remove(path.size() - 1); // backtrack
}
if (root.right != null) {
preOrderDfs(root.right, targetSum - root.val, res, path);
path.remove(path.size() - 1); // backtrack
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
// Method 2
class Solution {
List<List<Integer>> result;
LinkedList<Integer> path;
public List<List<Integer>> pathSum (TreeNode root,int targetSum) {
result = new LinkedList<>();
path = new LinkedList<>();
travesal(root, targetSum);
return result;
}
private void travesal(TreeNode root, int count) {
if (root == null) return;
path.offer(root.val);
count -= root.val;
if (root.left == null && root.right == null && count == 0) {
result.add(new LinkedList<>(path));
}
travesal(root.left, count);
travesal(root.right, count);
path.removeLast(); // backtrack
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// Method 3 Unified Iterative DFS
class Solution {
public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
List<List<Integer>> result = new ArrayList<>();
Stack<TreeNode> nodeStack = new Stack<>();
Stack<Integer> sumStack = new Stack<>();
Stack<ArrayList<Integer>> pathStack = new Stack<>();
if(root == null)
return result;
nodeStack.add(root);
sumStack.add(root.val);
pathStack.add(new ArrayList<>());
while(!nodeStack.isEmpty()){
TreeNode currNode = nodeStack.peek();
int currSum = sumStack.pop();
ArrayList<Integer> currPath = pathStack.pop();
if(currNode != null){
nodeStack.pop();
nodeStack.add(currNode);
nodeStack.add(null);
sumStack.add(currSum);
currPath.add(currNode.val);
pathStack.add(new ArrayList(currPath));
if(currNode.right != null){
nodeStack.add(currNode.right);
sumStack.add(currSum + currNode.right.val);
pathStack.add(new ArrayList(currPath));
}
if(currNode.left != null){
nodeStack.add(currNode.left);
sumStack.add(currSum + currNode.left.val);
pathStack.add(new ArrayList(currPath));
}
}else{
nodeStack.pop();
TreeNode temp = nodeStack.pop();
if(temp.left == null && temp.right == null && currSum == targetSum)
result.add(new ArrayList(currPath));
}
}
return result;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
# Python
- Path Sum
(version one) Recursion
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def traversal(self, cur: TreeNode, count: int) -> bool:
if not cur.left and not cur.right and count == 0: # found leaf and path sum is zero
return True
if not cur.left and not cur.right: # found leaf without valid path
return False
if cur.left: # Left
count -= cur.left.val
if self.traversal(cur.left, count): # recursive, process node
return True
count += cur.left.val # backtrack, undo process results
if cur.right: # Right
count -= cur.right.val
if self.traversal(cur.right, count): # recursive, process node
return True
count += cur.right.val # backtrack, undo process results
return False
def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
if root is None:
return False
return self.traversal(root, targetSum - root.val)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
(version two) Recursion + Refined
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
if not root:
return False
if not root.left and not root.right and targetSum == root.val:
return True
return self.hasPathSum(root.left, targetSum - root.val) or self.hasPathSum(root.right, targetSum - root.val)
2
3
4
5
6
7
8
9
10
11
12
13
(version three) Iteration
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
if not root:
return False
# Here the stack should contain pairs of <node pointer, path sum>
st = [(root, root.val)]
while st:
node, path_sum = st.pop()
# If the current node is a leaf node and the path sum equals `sum`, then return True
if not node.left and not node.right and path_sum == sum:
return True
# Right node: when pushing a node, also record the path sum
if node.right:
st.append((node.right, path_sum + node.right.val))
# Left node: when pushing a node, also record the path sum
if node.left:
st.append((node.left, path_sum + node.left.val))
return False
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
- Path Sum II
(version one) Recursion
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def __init__(self):
self.result = []
self.path = []
def traversal(self, cur, count):
if not cur.left and not cur.right and count == 0: # Reached leaf with targetSum path found
self.result.append(self.path[:])
return
if not cur.left and not cur.right: # Reached leaf with no targetSum path
return
if cur.left: # Left (skip null nodes)
self.path.append(cur.left.val)
count -= cur.left.val
self.traversal(cur.left, count) # recursive
count += cur.left.val # backtrack
self.path.pop() # backtrack
if cur.right: # Right (skip null nodes)
self.path.append(cur.right.val)
count -= cur.right.val
self.traversal(cur.right, count) # recursive
count += cur.right.val # backtrack
self.path.pop() # backtrack
return
def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:
self.result.clear()
self.path.clear()
if not root:
return self.result
self.path.append(root.val) # Add root to path
self.traversal(root, targetSum - root.val)
return self.result
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
(version two) Recursion + Refined
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def pathSum(self, root: Optional[TreeNode], targetSum: int) -> List[List[int]]:
result = []
self.traversal(root, targetSum, [], result)
return result
def traversal(self,node, count, path, result):
if not node:
return
path.append(node.val)
count -= node.val
if not node.left and not node.right and count == 0:
result.append(list(path))
self.traversal(node.left, count, path, result)
self.traversal(node.right, count, path, result)
path.pop()
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
