It is said that it can also be done using an iterative method

Iterative Traversal of Binary Tree

Thought Process

Why is it possible to implement preorder, inorder, and postorder traversals of a binary tree using an iterative method (non-recursive approach)?

In the article 1047.Remove All Adjacent Duplicates In String (opens new window), we mentioned that the implementation of recursion involves: each recursive call pushes the function's local variables, parameter values, and return addresses onto the call stack. When recursion returns, the stack's top is popped out with the previous parameters, which is why recursion can return to the previous level.

At this point, you should realize that we can also use a stack to implement the preorder, inorder, and postorder traversals of a binary tree.

Preorder Traversal (Iterative Method)

Let's first look at the preorder traversal.

Preorder traversal is in the order: center-left-right. We process the root node first, then push the right child, followed by the left child onto the stack.

Why push the right child before the left child? Because this ensures that when popping from the stack, the order is center-left-right.

The animation is as follows:

Based on this, the code can be written as follows: (Note that null nodes are not pushed onto the stack)

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> result;
        if (root == NULL) return result;
        st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();                       // Center
            st.pop();
            result.push_back(node->val);
            if (node->right) st.push(node->right);           // Right (null nodes are not pushed)
            if (node->left) st.push(node->left);             // Left (null nodes are not pushed)
        }
        return result;
    }
};

At this point, it might seem that writing a preorder traversal using the iterative method isn't hard. And indeed, it's not.

So, does this mean that by slightly modifying the preorder traversal code, we can derive the inorder traversal?

Actually, not quite!

But when we try to write the inorder traversal using the iterative method, we'll realize that the pattern is different from the one used for preorder traversal. The current preorder traversal logic cannot be directly applied to inorder traversal.

Inorder Traversal (Iterative Method)

To explain clearly, I'll describe that in the process of iteration, we actually have two operations:

1. Process: Add the element to the result array.
2. Visit: Traverse the node.

Analyzing why the earlier preorder traversal code cannot be generically used for inorder traversal, we notice that as preorder traversal orders as center-left-right, the nodes we visit first are the center nodes, and these are also the nodes we process, allowing the concise code structure, because the nodes to be visited and processed are the same, which is the center node.

Now, let's look at inorder traversal. In inorder traversal, the order is left-center-right. First, we visit the top node of the binary tree, then we go deeper level by level until we reach the bottom leftmost part of the tree, from there we begin processing the nodes (i.e., add nodes' values into the result array). This results in the inconsistency of process order and visit order.

Therefore, in writing iterative methods for inorder traversal, we need to leverage pointer traversal to help visit nodes, while the stack is used for processing the elements on the nodes.

The animation is as follows:

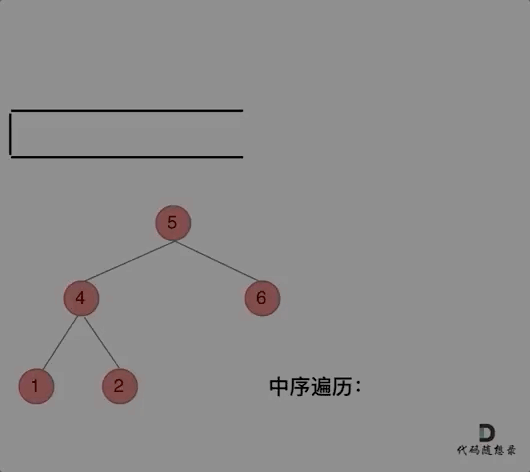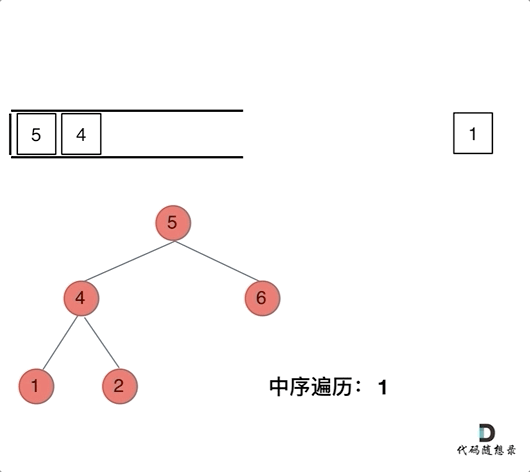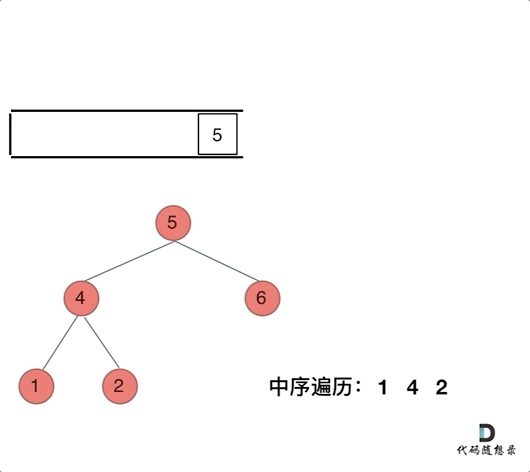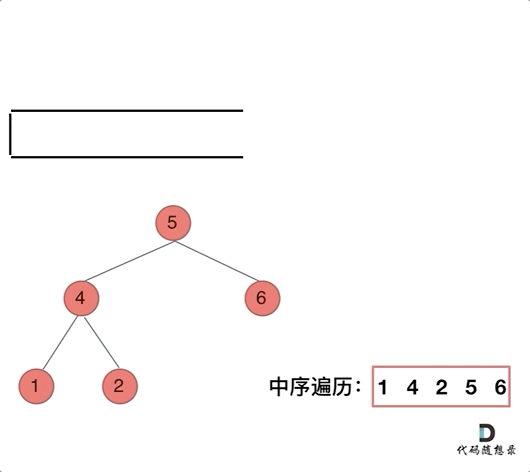
With this understanding, the code for inorder traversal can be written as:

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> st;
        TreeNode* cur = root;
        while (cur != NULL || !st.empty()) {
            if (cur != NULL) { // Using a pointer to access nodes, traversing to the bottom layer
                st.push(cur); // Push the accessed nodes onto the stack
                cur = cur->left;                // Left
            } else {
                cur = st.top(); // The data popped from the stack is what needs to be processed (added to the result array)
                st.pop();
                result.push_back(cur->val);     // Center
                cur = cur->right;               // Right
            }
        }
        return result;
    }
};

Postorder Traversal (Iterative Method)

Now let's look at postorder traversal. Preorder traversal is center-left-right, and postorder traversal is left-right-center. Thus, we merely need to adjust the order in which we push nodes for preorder traversal to a center-right-left order. Then by reversing the result array, the output order becomes left-right-center, as shown in the following figure:

So for postorder traversal, we only need to slightly modify the code for preorder traversal:

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> result;
        if (root == NULL) return result;
        st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();
            st.pop();
            result.push_back(node->val);
            if (node->left) st.push(node->left); // Compared to preorder traversal, modify the order of pushing (null nodes are not pushed)
            if (node->right) st.push(node->right); // null nodes are not pushed
        }
        reverse(result.begin(), result.end()); // Reversing the result yields left-right-center order
        return result;
    }
};

Summary

At this point, we have written the iterative implementations of preorder, inorder, and postorder traversal of a binary tree. You can see that preorder and inorder do not share a similar code style, unlike recursive methods, where slightly adjusting the code can implement preorder, inorder, and postorder.

This is because in preorder traversal, visiting a node (traversing a node) and processing a node (putting the element into the result array) can be synchronized, while it cannot be synchronized in an inorder traversal!

Some of you might not totally understand the above statement; it is recommended to try writing preorder traversal using iteration and then attempting inorder traversal to truly understand.

Then a question arises: Can't the iterative implementations for preorder, inorder, and postorder traversals of a binary tree be unified in style (meaning that changing the code in preorder creates the code for inorder and postorder)?

Of course, they can. This writing style, however, is not easy to understand, discussed in detail in the next article, stay tuned!

More Versions

Java:

// Preorder Traversal Order: Center-Left-Right, Stack Order: Center-Right-Left
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null){
            return result;
        }
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()){
            TreeNode node = stack.pop();
            result.add(node.val);
            if (node.right != null){
                stack.push(node.right);
            }
            if (node.left != null){
                stack.push(node.left);
            }
        }
        return result;
    }
}

// Inorder Traversal Order: Left-Center-Right, Stack Order: Left-Right
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null){
            return result;
        }
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;
        while (cur != null || !stack.isEmpty()){
           if (cur != null){
               stack.push(cur);
               cur = cur.left;
           }else{
               cur = stack.pop();
               result.add(cur.val);
               cur = cur.right;
           }
        }
        return result;
    }
}

// Postorder Traversal Order: Left-Right-Center, Stack Order: Center-Left-Right, Reverse Result at End
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null){
            return result;
        }
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()){
            TreeNode node = stack.pop();
            result.add(node.val);
            if (node.left != null){
                stack.push(node.left);
            }
            if (node.right != null){
                stack.push(node.right);
            }
        }
        Collections.reverse(result);
        return result;
    }
}

Python:

# Preorder Traversal - Iterative - LC144 Binary Tree Preorder Traversal
class Solution:
    def preorderTraversal(self, root: TreeNode) -> List[int]:
        # If the root node is empty, return an empty list
        if not root:
            return []
        stack = [root]
        result = []
        while stack:
            node = stack.pop()
            # Process the center node first
            result.append(node.val)
            # Push right child first
            if node.right:
                stack.append(node.right)
            # Push left child after
            if node.left:
                stack.append(node.left)
        return result

# Inorder Traversal - Iterative - LC94 Binary Tree Inorder Traversal
class Solution:
    def inorderTraversal(self, root: TreeNode) -> List[int]:

        if not root:
            return []
        stack = []  # Cannot add root node to stack early

        result = []
        cur = root
        while cur or stack:
            # First, iterate to visit the bottom-left node
            if cur:     
                stack.append(cur)
                cur = cur.left		
            # Process the stack top node after reaching the leftmost node    
            else:		
                cur = stack.pop()
                result.append(cur.val)
                # Take the right node of the stack top element
                cur = cur.right	
        return result

# Postorder Traversal - Iterative - LC145 Binary Tree Postorder Traversal
class Solution:
    def postorderTraversal(self, root: TreeNode) -> List[int]:
        if not root:
            return []
        stack = [root]
        result = []
        while stack:
            node = stack.pop()
            # Process the center node first
            result.append(node.val)
            # Push left child first
            if node.left:
                stack.append(node.left)
            # Push right child after
            if node.right:
                stack.append(node.right)
        # Flip the final array
        return result[::-1]

A New Iterative Solution for Postorder Traversal in Python:

• This solution, unlike the previously introduced method of flipping an adjusted preorder result, handles each node directly. This implementation method is unlikely to be written in an interview. In the next section, I will modify this code to provide a more concise, streamlined, and easier-to-implement unified method.

class Solution:
    def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        values = []
        stack = []
        popped_nodes = set() # Track nodes whose values have been harvested, this is key, nodes that have been harvested are still in the tree and can be visited, but logically they are equivalent to null.
        current = root

        while current or stack:
            if current: # Handles a node and its left and right children at once, does not handle grandchildren, grandchildren are handled by left and right children later.
                stack.append(current) # Stack itself

                if current.right:
                    stack.append(current.right) # Stack right child
                
                if current.left: # Since the stack is last-in, first-out, and postorder is 'left-right-center', the left child is added later.
                    stack.append(current.left) # Stack left child

                current = None # Leads to stack popping at A
                continue

            node = stack.pop() # A: If no left child, pop the right child, if no right child, pop itself.

            # If node is a leaf node, it can be harvested; if left and right children have been harvested, it can also be harvested
            if (node.left is None or node.left in popped_nodes) and \
                (node.right is None or node.right in popped_nodes):
                popped_nodes.add(node)
                values.append(node.val)
                continue
            
            current = node # Does not meet harvesting conditions, indicating that there are unstacked children under the node, so stack them.
        
        return values

Go:

Iterative Preorder Traversal

func preorderTraversal(root *TreeNode) []int {
    ans := []int{}

	if root == nil {
		return ans
	}

	st := list.New()
    st.PushBack(root)

    for st.Len() > 0 {
        node := st.Remove(st.Back()).(*TreeNode)

        ans = append(ans, node.Val)
        if node.Right != nil {
            st.PushBack(node.Right)
        }
        if node.Left != nil {
            st.PushBack(node.Left)
        }
    }
    return ans
}

Iterative Postorder Traversal

func postorderTraversal(root *TreeNode) []int {
    ans := []int{}

	if root == nil {
		return ans
	}

	st := list.New()
    st.PushBack(root)

    for st.Len() > 0 {
        node := st.Remove(st.Back()).(*TreeNode)

        ans = append(ans, node.Val)
        if node.Left != nil {
            st.PushBack(node.Left)
        }
        if node.Right != nil {
            st.PushBack(node.Right)
        }
    }
    reverse(ans)
    return ans
}

func reverse(a []int) {
    l, r := 0, len(a) - 1
    for l < r {
        a[l], a[r] = a[r], a[l]
        l, r = l+1, r-1
    }
}

Iterative Inorder Traversal

func inorderTraversal(root *TreeNode) []int {
    ans := []int{}
    if root == nil {
        return ans
    }

    st := list.New()
    cur := root

    for cur != nil || st.Len() > 0 {
        if cur != nil {
            st.PushBack(cur)
            cur = cur.Left
        } else {
            cur = st.Remove(st.Back()).(*TreeNode)
            ans = append(ans, cur.Val)
            cur = cur.Right
        }
    }

    return ans
}

JavaScript:

Preorder Traversal:

// Stack: Right -> Left
// Pop: Center -> Left -> Right
var preorderTraversal = function(root, res = []) {
    if(!root) return res;
    const stack = [root];
    let cur = null;
    while(stack.length) {
        cur = stack.pop();
        res.push(cur.val);
        cur.right && stack.push(cur.right);
        cur.left && stack.push(cur.left);
    }
    return res;
};

Inorder Traversal:

// Stack: Left -> Right
// Pop: Left -> Center -> Right

var inorderTraversal = function(root, res = []) {
    const stack = [];
    let cur = root;
    while(stack.length || cur) {
        if(cur) {
            stack.push(cur);
            // Left
            cur = cur.left;
        } else {
            // --> Pop center
            cur = stack.pop();
            res.push(cur.val); 
            // Right
            cur = cur.right;
        }
    };
    return res;
};

Postorder Traversal:

// Stack: Left -> Right
// Pop: Center -> Right -> Left, Reverse result at end

var postorderTraversal = function(root, res = []) {
    if (!root) return res;
    const stack = [root];
    let cur = null;
    do {
        cur = stack.pop();
        res.push(cur.val);
        cur.left && stack.push(cur.left);
        cur.right && stack.push(cur.right);
    } while(stack.length);
    return res.reverse();
};

TypeScript:

// Iterative Preorder Traversal
function preorderTraversal(root: TreeNode | null): number[] {
    if (root === null) return [];
    let res: number[] = [];
    let helperStack: TreeNode[] = [];
    let curNode: TreeNode = root;
    helperStack.push(curNode);
    while (helperStack.length > 0) {
        curNode = helperStack.pop()!;
        res.push(curNode.val);
        if (curNode.right !== null) helperStack.push(curNode.right);
        if (curNode.left !== null) helperStack.push(curNode.left);
    }
    return res;
};

// Iterative Inorder Traversal
function inorderTraversal(root: TreeNode | null): number[] {
    let helperStack: TreeNode[] = [];
    let res: number[] = [];
    if (root === null) return res;
    let curNode: TreeNode | null = root;
    while (curNode !== null || helperStack.length > 0) {
        if (curNode !== null) {
            helperStack.push(curNode);
            curNode = curNode.left;
        } else {
            curNode = helperStack.pop()!;
            res.push(curNode.val);
            curNode = curNode.right;
        }
    }
    return res;
};

// Iterative Postorder Traversal
function postorderTraversal(root: TreeNode | null): number[] {
    let helperStack: TreeNode[] = [];
    let res: number[] = [];
    let curNode: TreeNode;
    if (root === null) return res;
    helperStack.push(root);
    while (helperStack.length > 0) {
        curNode = helperStack.pop()!;
        res.push(curNode.val);
        if (curNode.left !== null) helperStack.push(curNode.left);
        if (curNode.right !== null) helperStack.push(curNode.right);
    }
    return res.reverse();
};

Swift：

// Iterative Preorder Traversal
func preorderTraversal(_ root: TreeNode?) -> [Int] {
    var result = [Int]()
    guard let root = root else { return result }
    var stack = [root]
    while !stack.isEmpty {
        let current = stack.removeLast()
        // Push right first, then left, so popping is in left-right order
        if let node = current.right { // Right
            stack.append(node)
        }
        if let node = current.left { // Left
            stack.append(node)
        }
        result.append(current.val) // Center
    }
    return result
}

// Iterative Postorder Traversal
func postorderTraversal(_ root: TreeNode?) -> [Int] {
    var result = [Int]()
    guard let root = root else { return result }
    var stack = [root]
    while !stack.isEmpty {
        let current = stack.removeLast()
        // Unlike preorder, which is changed to center-right-left, the final result needs to be reversed to get postorder
        if let node = current.left { // Left
            stack.append(node)
        }
        if let node = current.right { // Right
            stack.append(node)
        }
        result.append(current.val) // Center
    }
    return result.reversed()
}

// Iterative Inorder Traversal
func inorderTraversal(_ root: TreeNode?) -> [Int] {
    var result = [Int]()
    var stack = [TreeNode]()
    var current: TreeNode! = root
    while current != nil || !stack.isEmpty {
        if current != nil { // Visit down to the leftmost leaf
            stack.append(current)
            current = current.left // Left
        } else {
            current = stack.removeLast()
            result.append(current.val) // Center
            current = current.right // Right
        }
    }
    return result
}

Scala:

// Preorder Traversal (Iterative Method)
object Solution {
  import scala.collection.mutable
  def preorderTraversal(root: TreeNode): List[Int] = {
    val res = mutable.ListBuffer[Int]()
    if (root == null) return res.toList
    // Declare a stack with a TreeNode generic
    val stack = mutable.Stack[TreeNode]()
    stack.push(root) // Push the root node first
    while (!stack.isEmpty) {
      var curNode = stack.pop()
      res.append(curNode.value) // Push this value onto the stack
      // If the current node's left and right nodes are not null, push them onto the stack, first right, then left
      if (curNode.right != null) stack.push(curNode.right)
      if (curNode.left != null) stack.push(curNode.left)
    }
    res.toList
  }
}

// Inorder Traversal (Iterative Method)
object Solution {
  import scala.collection.mutable
  def inorderTraversal(root: TreeNode): List[Int] = {
    val res = mutable.ArrayBuffer[Int]()
    if (root == null) return res.toList
    val stack = mutable.Stack[TreeNode]()
    var curNode = root
    // Push all left nodes onto the stack until reaching null, at which point the top of the stack is popped and added to the result.
    // Then, add the right node of the stack top element and continue iterating
    while (curNode != null || !stack.isEmpty) {
      if (curNode != null) {
        stack.push(curNode)
        curNode = curNode.left
      } else {
        curNode = stack.pop()
        res.append(curNode.value)
        curNode = curNode.right
      }
    }
    res.toList
  }
}

// Postorder Traversal (Iterative Method)
object Solution {
  import scala.collection.mutable
  def postorderTraversal(root: TreeNode): List[Int] = {
    val res = mutable.ListBuffer[Int]()
    if (root == null) return res.toList
    val stack = mutable.Stack[TreeNode]()
    stack.push(root)
    while (!stack.isEmpty) {
      val curNode = stack.pop()
      res.append(curNode.value)
      // Here, the left node is pushed first, followed by the right node
      if(curNode.left != null) stack.push(curNode.left)
      if(curNode.right != null) stack.push(curNode.right)
    }
    // Finally, reverse the List
    res.reverse.toList
  }
}

Rust:

use std::cell::RefCell;
use std::rc::Rc;
impl Solution {
    //Preorder
    pub fn preorder_traversal(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<i32> {
        let mut res = vec![];
        let mut stack = vec![root];
        while !stack.is_empty() {
            if let Some(node) = stack.pop().unwrap() {
                res.push(node.borrow().val);
                stack.push(node.borrow().right.clone());
                stack.push(node.borrow().left.clone());
            }
        }
        res
    }
    //Inorder
    pub fn inorder_traversal(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<i32> {
        let mut res = vec![];
        let mut stack = vec![];
        let mut node = root;

        while !stack.is_empty() || node.is_some() {
            while let Some(n) = node {
                node = n.borrow().left.clone();
                stack.push(n);
            }
            if let Some(n) = stack.pop() {
                res.push(n.borrow().val);
                node = n.borrow().right.clone();
            }
        }
        res
    }
    //Postorder
    pub fn postorder_traversal(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<i32> {
        let mut res = vec![];
        let mut stack = vec![root];
        while !stack.is_empty() {
            if let Some(node) = stack.pop().unwrap() {
                res.push(node.borrow().val);
                stack.push(node.borrow().left.clone());
                stack.push(node.borrow().right.clone());
            }
        }
        res.into_iter().rev().collect()
    }
}

C#

// Preorder Traversal
public IList<int> PreorderTraversal(TreeNode root)
{
    var st = new Stack<TreeNode>();
    var res = new List<int>();
    if (root == null) return res;
    st.Push(root);
    while (st.Count != 0)
    {
        var node = st.Pop();
        res.Add(node.val);
        if (node.right != null)
            st.Push(node.right);
        if (node.left != null)
            st.Push(node.left);
    }
    return res;
}  

// Inorder Traversal
public IList<int> InorderTraversal(TreeNode root)
{
    var st = new Stack<TreeNode>();
    var res = new List<int>();
    var cur = root;
    while (st.Count != 0 || cur != null)
    {
        if (cur != null)
        {
            st.Push(cur);
            cur = cur.left;
        }
        else
        {
            cur = st.Pop();
            res.Add(cur.val);
            cur = cur.right;
        }
    }
    return res;
}
// Postorder Traversal
public IList<int> PostorderTraversal(TreeNode root)
{
    var res = new List<int>();
    var st = new Stack<TreeNode>();
    if (root == null) return res;
    st.Push(root);
    while (st.Count != 0)
    {
        var cur = st.Pop();
        res.Add(cur.val);
        if (cur.left != null) st.Push(cur.left);
        if (cur.right != null) st.Push(cur.right);
    }
    res.Reverse(0, res.Count());
    return res;
}