keetcoder

# 235. Lowest Common Ancestor of a Binary Search Tree

LeetCode Problem Link (opens new window)

Given a binary search tree (BST), find the lowest common ancestor (LCA) of two specified nodes in the BST.

According to the definition in Baidu Encyclopedia: “For the root tree T, the LCA of two nodes p and q is defined as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”

Example given the following BST: root = [6,2,8,0,4,7,9,null,null,3,5]

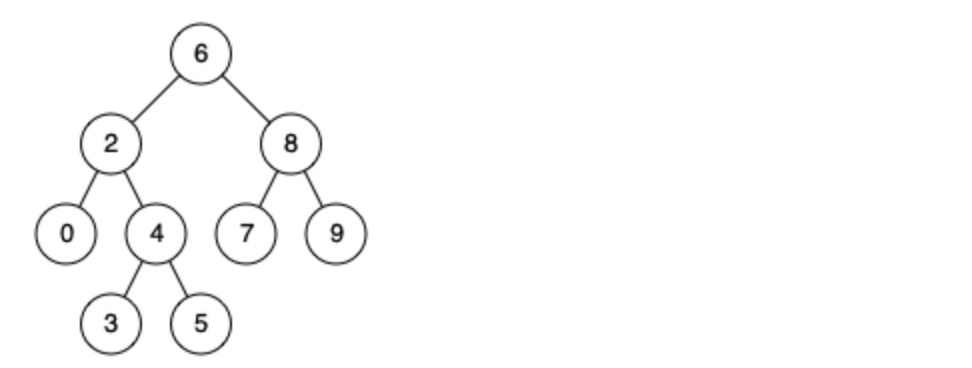
235. Lowest Common Ancestor of a Binary Search Tree

Example 1:

  • Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
  • Output: 6
  • Explanation: The LCA of nodes 2 and 8 is 6.

Example 2:

  • Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
  • Output: 2
  • Explanation: The LCA of nodes 2 and 4 is 2 since a node can be a descendant of itself as per the definition.

Note:

  • All nodes' values are unique.
  • p and q are different nodes and both of them exist in the BST.

# Thought Process

If you have solved the 0236.Lowest Common Ancestor of a Binary Tree (opens new window), you would know that finding common ancestors can involve backtracking from the bottom up, where a node whose left subtree contains p and right subtree contains q would be the LCA.

This problem, however, is different because it's a binary search tree, which has ordered nodes. We can take advantage of this characteristic.

In an ordered tree, how do you know if p is in the left subtree of a node and q in the right?

Since it's an ordered tree, if a node is the common ancestor, its value must be within the range [p, q]. In other words, a node is the LCA if node > p && node < q or node > q && node < p.

Thus, while traversing from the top down, the first time we encounter a node falling within the value range [p.val, q.val], it can be concluded that this node is the LCA of p and q.

Consider moving through the tree as follows:

Example:

  • If p = 6 and q = 9:

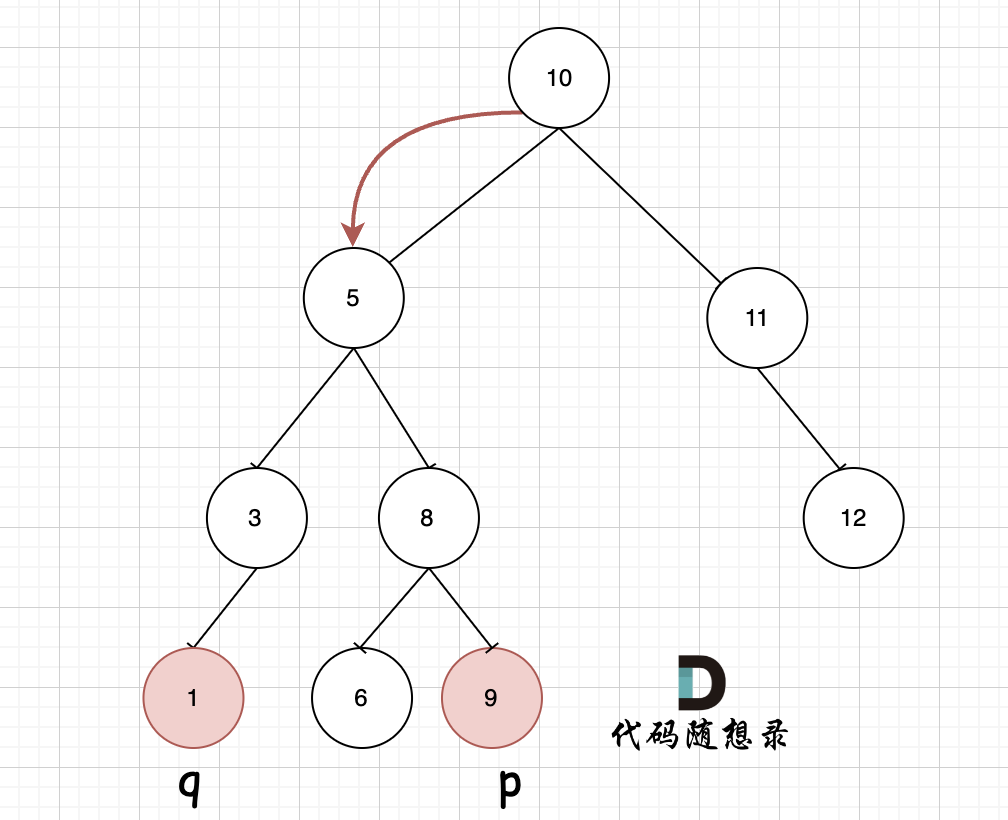
235. Lowest Common Ancestor of a Binary Search Tree 2

Following the directed path will directly locate node 8 as the LCA efficiently without traversing the entire tree.

# Recursive Approach

Following the three-step recursive breakdown:

  • Define the Recursive Function's Return Value and Parameters

The parameters will be the current node and two nodes p, q.

The return value should be the LCA node, hence TreeNode *.

Code:

TreeNode* traverse(TreeNode* current, TreeNode* p, TreeNode* q)
1
  • Define the Termination Condition

Returning when encountering a null node is adequate:

if (current == NULL) return current;
1

For this problem, encountering a null node is not possible since it is guaranteed p and q exist in the tree.

  • Define Logic within a Single Recursive Layer

While traversing the BST, the key is to look for the range [p->val, q->val] (or [q->val, p->val]).

If the current node val is greater than both p.val and q.val, move left (implying the target range is on the left subtree).

Code:

if (current->val > p->val && current->val > q->val) {
    TreeNode* left = traverse(current->left, p, q);
    if (left != NULL) {
        return left;
    }
}
1
2
3
4
5
6

The recursion here involves returning early upon finding a non-null result as shown above.

If the current node val is smaller than both p.val and q.val, move right (target range on the right subtree).

if (current->val < p->val && current->val < q->val) {
    TreeNode* right = traverse(current->right, p, q);
    if (right != NULL) {
        return right;
    }
}
1
2
3
4
5
6

In remaining scenarios where the current node's value falls into (p->val <= current->val && current->val <= q->val) or the opposite, the current node is the LCA. Return current:

return current;
1

Full recursive code:

class Solution {
private:
    TreeNode* traverse(TreeNode* current, TreeNode* p, TreeNode* q) {
        if (current == nullptr) return current;
                                                        
        if (current->val > p->val && current->val > q->val) {
            TreeNode* left = traverse(current->left, p, q);
            if (left != nullptr) {
                return left;
            }
        }

        if (current->val < p->val && current->val < q->val) {
            TreeNode* right = traverse(current->right, p, q);
            if (right != nullptr) {
                return right;
            }
        }
        return current;
    }
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        return traverse(root, p, q);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

Simplified code:

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if (root->val > p->val && root->val > q->val) {
            return lowestCommonAncestor(root->left, p, q);
        } else if (root->val < p->val && root->val < q->val) {
            return lowestCommonAncestor(root->right, p, q);
        } else return root;
    }
};
1
2
3
4
5
6
7
8
9
10

# Iterative Approach

Adopting the iterative approach for BST is straightforward due to its ordered nature, as previously elaborated in 0700.Search in a Binary Search Tree (opens new window).

Iterative code:

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        while(root) {
            if (root->val > p->val && root->val > q->val) {
                root = root->left;
            } else if (root->val < p->val && root->val < q->val) {
                root = root->right;
            } else return root;
        }
        return nullptr;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13

The simplicity of the iterative approach, leveraging the order inherent in BSTs, should be clear.

# Conclusion

The LCA problem in binary search trees is more straightforward compared to 0236.Lowest Common Ancestor of a Binary Tree (opens new window). The BST's directionality facilitates direct traversal to locate the LCA upon encountering a node within the specified range.

Additionally, the iterative approach is even more intuitive than the recursive, again owing to the tree's ordering.

# Other Language Versions

# Java

Recursive approach:

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root.val > p.val && root.val > q.val) return lowestCommonAncestor(root.left, p, q);
        if (root.val < p.val && root.val < q.val) return lowestCommonAncestor(root.right, p, q);
        return root;
    }
}
1
2
3
4
5
6
7

Iterative approach:

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        while (true) {
            if (root.val > p.val && root.val > q.val) {
                root = root.left;
            } else if (root.val < p.val && root.val < q.val) {
                root = root.right;
            } else {
                break;
            }
        }
        return root;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

# Python

Recursive approach (Version 1)

class Solution:
    def traverse(self, cur, p, q):
        if cur is None:
            return cur
                                                       
        if cur.val > p.val and cur.val > q.val:          
            left = self.traverse(cur.left, p, q)
            if left is not None:
                return left

        if cur.val < p.val and cur.val < q.val:           
            right = self.traverse(cur.right, p, q)
            if right is not None:
                return right

        return cur

    def lowestCommonAncestor(self, root, p, q):
        return self.traverse(root, p, q)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

Recursive approach (Version 2) Simplified

class Solution:
    def lowestCommonAncestor(self, root, p, q):
        if root.val > p.val and root.val > q.val:
            return self.lowestCommonAncestor(root.left, p, q)
        elif root.val < p.val and root.val < q.val:
            return self.lowestCommonAncestor(root.right, p, q)
        else:
            return root
1
2
3
4
5
6
7
8
9

Iterative approach

class Solution:
    def lowestCommonAncestor(self, root, p, q):
        while root:
            if root.val > p.val and root.val > q.val:
                root = root.left
            elif root.val < p.val and root.val < q.val:
                root = root.right
            else:
                return root
        return None
1
2
3
4
5
6
7
8
9
10

# Go

Recursive approach

func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
    if root.Val > p.Val && root.Val > q.Val {
        return lowestCommonAncestor(root.Left, p, q)
    } else if root.Val < p.Val && root.Val < q.Val {
        return lowestCommonAncestor(root.Right, p, q)
    } else {
        return root
    }
}
1
2
3
4
5
6
7
8
9

Iterative approach

func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
    for root != nil {
        if root.Val > p.Val && root.Val > q.Val {
            root = root.Left
        } else if root.Val < p.Val && root.Val < q.Val {
            root = root.Right
        } else {
            return root
        }
    }
    return nil
}
1
2
3
4
5
6
7
8
9
10
11
12

# JavaScript

Recursive approach:

var lowestCommonAncestor = function(root, p, q) {
    if(root === null) {
        return root;
    }
    if(root.val > p.val && root.val > q.val) {
         return root.left = lowestCommonAncestor(root.left,p,q);
    }
    if(root.val < p.val && root.val < q.val) {
        return root.right = lowestCommonAncestor(root.right,p,q);
    }
    return root;
};
1
2
3
4
5
6
7
8
9
10
11
12

Iterative approach

var lowestCommonAncestor = function(root, p, q) {
    while(root) {
        if(root.val > p.val && root.val > q.val) {
            root = root.left;
        }else if(root.val < p.val && root.val < q.val) {
            root = root.right;
        }else {
            return root;
        }
        
    }
    return null;
};
1
2
3
4
5
6
7
8
9
10
11
12
13

# TypeScript

Recursive approach:

function lowestCommonAncestor(root: TreeNode | null, p: TreeNode | null, q: TreeNode | null): TreeNode | null {
    if (root.val > p.val && root.val > q.val)
        return lowestCommonAncestor(root.left, p, q);
    if (root.val < p.val && root.val < q.val)
        return lowestCommonAncestor(root.right, p, q);
    return root;
};
1
2
3
4
5
6
7

Iterative approach:

function lowestCommonAncestor(root: TreeNode | null, p: TreeNode | null, q: TreeNode | null): TreeNode | null {
    while (root !== null) {
        if (root.val > p.val && root.val > q.val) {
            root = root.left;
        } else if (root.val < p.val && root.val < q.val) {
            root = root.right;
        } else {
            return root;
        };
    };
    return null;
};
1
2
3
4
5
6
7
8
9
10
11
12

# Scala

Recursive:

object Solution {
  def lowestCommonAncestor(root: TreeNode, p: TreeNode, q: TreeNode): TreeNode = {
    if (root.value > p.value && root.value > q.value) lowestCommonAncestor(root.left, p, q)
    else if (root.value < p.value && root.value < q.value) lowestCommonAncestor(root.right, p, q)
    else root
  }
}
1
2
3
4
5
6
7

Iterative:

object Solution {
  def lowestCommonAncestor(root: TreeNode, p: TreeNode, q: TreeNode): TreeNode = {
    var curNode = root 
    while(curNode != null){
      if(curNode.value > p.value && curNode.value > q.value) curNode = curNode.left
      else if(curNode.value < p.value && curNode.value < q.value) curNode = curNode.right
      else return curNode
    }
    null
  }
}
1
2
3
4
5
6
7
8
9
10
11

# Rust

Recursive:

impl Solution {
    pub fn lowest_common_ancestor(
        root: Option<Rc<RefCell<TreeNode>>>,
        p: Option<Rc<RefCell<TreeNode>>>,
        q: Option<Rc<RefCell<TreeNode>>>,
    ) -> Option<Rc<RefCell<TreeNode>>> {
        let q_val = q.as_ref().unwrap().borrow().val;
        let p_val = p.as_ref().unwrap().borrow().val;
        let root_val = root.as_ref().unwrap().borrow().val;

        if root_val > q_val && root_val > p_val {
            return Self::lowest_common_ancestor(
                root.as_ref().unwrap().borrow().left.clone(),
                p,
                q,
            );
        };

        if root_val < q_val && root_val < p_val {
            return Self::lowest_common_ancestor(
                root.as_ref().unwrap().borrow().right.clone(),
                p,
                q,
            );
        }
        root
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

Iterative:

impl Solution {
    pub fn lowest_common_ancestor(
        mut root: Option<Rc<RefCell<TreeNode>>>,
        p: Option<Rc<RefCell<TreeNode>>>,
        q: Option<Rc<RefCell<TreeNode>>>,
    ) -> Option<Rc<RefCell<TreeNode>>> {
        let p_val = p.unwrap().borrow().val;
        let q_val = q.unwrap().borrow().val;
        while let Some(node) = root.clone() {
            let root_val = node.borrow().val;
            if root_val > q_val && root_val > p_val {
                root = node.borrow().left.clone();
            } else if root_val < q_val && root_val < p_val {
                root = node.borrow().right.clone();
            } else {
                return root;
            }
        }
        None
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

# C#

Recursive:

public TreeNode LowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q)
{
    if (root.val > p.val && root.val > q.val)
        return LowestCommonAncestor(root.left, p, q);
    if (root.val < p.val && root.val < q.val)
        return LowestCommonAncestor(root.right, p, q);
    return root;
}
1
2
3
4
5
6
7
8

Iterative:

public TreeNode LowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q)
{
    while (root != null)
    {
        if (root.val > p.val && root.val > q.val)
            root = root.left;
        else if (root.val < p.val && root.val < q.val)
            root = root.right;
        else return root;
    }
    return null;
}
1
2
3
4
5
6
7
8
9
10
11
12
Last updated:: 9/4/2025, 3:19:38 PM

← 25. Insert into a Binary Search Tree →

Copyright © 2025 keetcoder