# 106. Construct Binary Tree from Inorder and Postorder Traversal
LeetCode Problem Link (opens new window)
Construct a binary tree from its inorder and postorder traversal arrays.
Note: You can assume that there are no duplicate elements in the tree.
For example, given
- Inorder traversal inorder = [9,3,15,20,7]
- Postorder traversal postorder = [9,15,7,20,3]
It returns the following binary tree:

# Solution
First, recall how to construct a unique binary tree using two sequences. The theoretical knowledge should be clear to everyone—it comes from taking the last element of the postorder array as the chopping point, then slicing the inorder array, and thereafter slicing the postorder array based on the inorder array. Each slice indicates a recursive call, wherein the last element of the postorder array will always supply the node value.
If you let us look at two sequences and draw a binary tree, it should just be a matter of minutes to draw it.
The process is illustrated in the following figure:
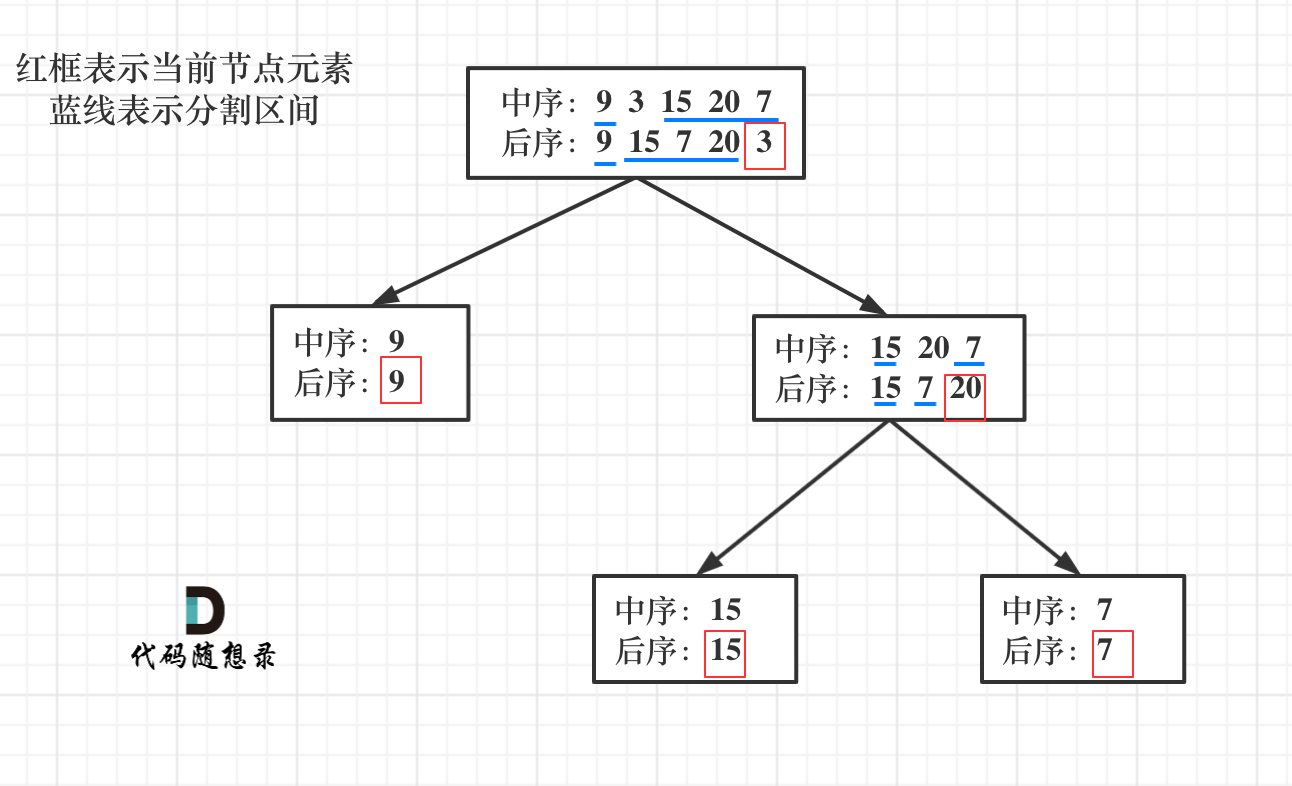
How do we convert this procedure into code?
When discussing slicing layer by layer, you should have thought of recursion. Let's walk through the solution steps:
Step 1: If the array size is zero, it indicates an empty node.
Step 2: If not empty, take the last element of the postorder array for the current node.
Step 3: Locate the last element of the postorder array in the inorder array and use it as the split point.
Step 4: Slice the inorder array into left and right subarrays. (Remember to first slice the inorder array.)
Step 5: Slice the postorder array into left and right subarrays.
Step 6: Reorganize the left and right subarrays recursively.
Given the above steps, writing the code should not be hard. Let's first establish a framework:
TreeNode* traversal (vector<int>& inorder, vector<int>& postorder) {
// Step 1
if (postorder.size() == 0) return NULL;
// Step 2: The last element of the postorder array is the root node
int rootValue = postorder[postorder.size() - 1];
TreeNode* root = new TreeNode(rootValue);
// Leaf node
if (postorder.size() == 1) return root;
// Step 3: Locate the delimiter in the inorder array
int delimiterIndex;
for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
if (inorder[delimiterIndex] == rootValue) break;
}
// Step 4: Slice inorder array into left and right
// Step 5: Slice postorder array into left and right
// Step 6
root->left = traversal(leftInorder, leftPostorder);
root->right = traversal(rightInorder, rightPostorder);
return root;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
The main challenge is cutting the array correctly—boundary values are easy to mess up.
Ensure to establish the slicing standard, whether using left-closed and right-open, left-open and right-closed, or left-closed and right-closed intervals. This invariance must be maintained through recursion.
Slicing involves four subarrays. Losing track of the invariance, with differing open and closed intervals, might easily lead to confusion!
I've emphasized the importance of loop invariants, whether in binary search as in 0035.Search Insert Position (opens new window), or even the algorithm for spirals in 0059.Spiral Matrix II (opens new window). Maintain your invariance at all costs—this problem is no different.
Start slicing the inorder array. Why begin with slicing the inorder array?
Because the split point is determined by the last element of the postorder array, which cuts the inorder array, hence slicing the inorder array is necessary.
Take care to adhere to the left-closed and right-open principles when splitting:
// Locate the split point in inorder
int delimiterIndex;
for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
if (inorder[delimiterIndex] == rootValue) break;
}
// Left-closed right-open interval: [0, delimiterIndex)
vector<int> leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);
// [delimiterIndex + 1, end)
vector<int> rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end() );
2
3
4
5
6
7
8
9
10
Next, slice the postorder array.
Omit the last element of the postorder array; as it serves as the central node, it's already been utilized.
How can we find the split points of the postorder array?
The postorder lacks a clear split point like the inorder. Unlike the inorder, which splits through a defined delimiter point, the postorder splits based on the size of the left subtree derived from the inorder array.
A key principle: the sizes of the inorder and postorder arrays must be identical (this is inevitable).
Having sliced the inorder into left and right sequences, we can use the left inorder array's size to correctly split the postorder array into left and right sequences.
// postorder ignores last element as it's been set as a node
postorder.resize(postorder.size() - 1);
// Adhering to left-closed right-open; using left inorder size as split
// [0, leftInorder.size)
vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
// [leftInorder.size(), end)
vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());
2
3
4
5
6
7
8
At this point, we've sliced the inorder array into left and right components, and similarly, the postorder array into left and right portions.
Now, let's write the recursive calls:
root->left = traversal(leftInorder, leftPostorder);
root->right = traversal(rightInorder, rightPostorder);
2
Here's the complete code:
class Solution {
private:
TreeNode* traversal (vector<int>& inorder, vector<int>& postorder) {
if (postorder.size() == 0) return NULL;
// Last element of postorder is the root node
int rootValue = postorder[postorder.size() - 1];
TreeNode* root = new TreeNode(rootValue);
// Leaf node
if (postorder.size() == 1) return root;
// Locate delimiter
int delimiterIndex;
for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
if (inorder[delimiterIndex] == rootValue) break;
}
// Slice inorder into left and right
vector<int> leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);
vector<int> rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end() );
// Omit last element from postorder
postorder.resize(postorder.size() - 1);
// Slice postorder
vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());
root->left = traversal(leftInorder, leftPostorder);
root->right = traversal(rightInorder, rightPostorder);
return root;
}
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
if (inorder.size() == 0 || postorder.size() == 0) return NULL;
return traversal(inorder, postorder);
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
I trust everyone, even if this is clear in mind, will face issues when coding it out. So it's crucial to add logs for debugging—to see if the array slicing aligns with one's understanding, without resorting to mental simulation, which tends to complicate the matter further.
Here’s the code with debugging logs: (Do not submit this log-added version on LeetCode, as it is prone to timeout.)
class Solution {
private:
TreeNode* traversal (vector<int>& inorder, vector<int>& postorder) {
if (postorder.size() == 0) return NULL;
int rootValue = postorder[postorder.size() - 1];
TreeNode* root = new TreeNode(rootValue);
if (postorder.size() == 1) return root;
int delimiterIndex;
for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
if (inorder[delimiterIndex] == rootValue) break;
}
vector<int> leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);
vector<int> rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end() );
postorder.resize(postorder.size() - 1);
vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());
// Debug logs
cout << "----------" << endl;
cout << "leftInorder :";
for (int i : leftInorder) {
cout << i << " ";
}
cout << endl;
cout << "rightInorder :";
for (int i : rightInorder) {
cout << i << " ";
}
cout << endl;
cout << "leftPostorder :";
for (int i : leftPostorder) {
cout << i << " ";
}
cout << endl;
cout << "rightPostorder :";
for (int i : rightPostorder) {
cout << i << " ";
}
cout << endl;
root->left = traversal(leftInorder, leftPostorder);
root->right = traversal(rightInorder, rightPostorder);
return root;
}
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
if (inorder.size() == 0 || postorder.size() == 0) return NULL;
return traversal(inorder, postorder);
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
The code's performance can be improved since it declares new vectors at each recursion level, consuming time and space, though it offers clarity and is designed to ensure understanding.
Here's a more efficient code reusing index pointers instead of declaring multiple vectors at each step. (The logic remains the same, just fewer variable declarations.)
class Solution {
private:
// Inorder interval: [inorderBegin, inorderEnd), Postorder interval: [postorderBegin, postorderEnd)
TreeNode* traversal (vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& postorder, int postorderBegin, int postorderEnd) {
if (postorderBegin == postorderEnd) return NULL;
int rootValue = postorder[postorderEnd - 1];
TreeNode* root = new TreeNode(rootValue);
if (postorderEnd - postorderBegin == 1) return root;
int delimiterIndex;
for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {
if (inorder[delimiterIndex] == rootValue) break;
}
// Slice inorder array
int leftInorderBegin = inorderBegin;
int leftInorderEnd = delimiterIndex;
int rightInorderBegin = delimiterIndex + 1;
int rightInorderEnd = inorderEnd;
// Slice postorder array
int leftPostorderBegin = postorderBegin;
int leftPostorderEnd = postorderBegin + delimiterIndex - inorderBegin;
int rightPostorderBegin = postorderBegin + (delimiterIndex - inorderBegin);
int rightPostorderEnd = postorderEnd - 1;
root->left = traversal(inorder, leftInorderBegin, leftInorderEnd, postorder, leftPostorderBegin, leftPostorderEnd);
root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, postorder, rightPostorderBegin, rightPostorderEnd);
return root;
}
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
if (inorder.size() == 0 || postorder.size() == 0) return NULL;
return traversal(inorder, 0, inorder.size(), postorder, 0, postorder.size());
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
Again, here is the version with debugging logs added: (Do not submit this log-added version on LeetCode, as it is prone to timeout.)
class Solution {
private:
TreeNode* traversal (vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& postorder, int postorderBegin, int postorderEnd) {
if (postorderBegin == postorderEnd) return NULL;
int rootValue = postorder[postorderEnd - 1];
TreeNode* root = new TreeNode(rootValue);
if (postorderEnd - postorderBegin == 1) return root;
int delimiterIndex;
for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {
if (inorder[delimiterIndex] == rootValue) break;
}
// Slice inorder array
int leftInorderBegin = inorderBegin;
int leftInorderEnd = delimiterIndex;
int rightInorderBegin = delimiterIndex + 1;
int rightInorderEnd = inorderEnd;
// Slice postorder array
int leftPostorderBegin = postorderBegin;
int leftPostorderEnd = postorderBegin + delimiterIndex - inorderBegin;
int rightPostorderBegin = postorderBegin + (delimiterIndex - inorderBegin);
int rightPostorderEnd = postorderEnd - 1;
cout << "----------" << endl;
cout << "leftInorder :";
for (int i = leftInorderBegin; i < leftInorderEnd; i++) {
cout << inorder[i] << " ";
}
cout << endl;
cout << "rightInorder :";
for (int i = rightInorderBegin; i < rightInorderEnd; i++) {
cout << inorder[i] << " ";
}
cout << endl;
cout << "leftpostorder :";
for (int i = leftPostorderBegin; i < leftPostorderEnd; i++) {
cout << postorder[i] << " ";
}
cout << endl;
cout << "rightpostorder :";
for (int i = rightPostorderBegin; i < rightPostorderEnd; i++) {
cout << postorder[i] << " ";
}
cout << endl;
root->left = traversal(inorder, leftInorderBegin, leftInorderEnd, postorder, leftPostorderBegin, leftPostorderEnd);
root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, postorder, rightPostorderBegin, rightPostorderEnd);
return root;
}
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
if (inorder.size() == 0 || postorder.size() == 0) return NULL;
return traversal(inorder, 0, inorder.size(), postorder, 0, postorder.size());
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
# Related Problem
# 105. Construct Binary Tree from Preorder and Inorder Traversal
LeetCode Problem Link (opens new window)
Build a binary tree from its preorder and inorder traversal arrays.
Note: You can assume that there are no duplicate elements in the tree.
For example, given
Preorder traversal preorder = [3,9,20,15,7] Inorder traversal inorder = [9,3,15,20,7]
It returns the following binary tree:

# Solution
This problem follows the same concept as problem 106.
I’ll directly present the code.
Below is the C++ code with debugging logs: (Note: This version is used for debugging purposes only and should not be submitted to LeetCode as it may cause timeout.)
class Solution {
private:
TreeNode* traversal (vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& preorder, int preorderBegin, int preorderEnd) {
if (preorderBegin == preorderEnd) return NULL;
int rootValue = preorder[preorderBegin];
TreeNode* root = new TreeNode(rootValue);
if (preorderEnd - preorderBegin == 1) return root;
int delimiterIndex;
for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {
if (inorder[delimiterIndex] == rootValue) break;
}
// Slice inorder array
int leftInorderBegin = inorderBegin;
int leftInorderEnd = delimiterIndex;
int rightInorderBegin = delimiterIndex + 1;
int rightInorderEnd = inorderEnd;
// Slice preorder array
int leftPreorderBegin = preorderBegin + 1;
int leftPreorderEnd = preorderBegin + 1 + delimiterIndex - inorderBegin;
int rightPreorderBegin = preorderBegin + 1 + (delimiterIndex - inorderBegin);
int rightPreorderEnd = preorderEnd;
cout << "----------" << endl;
cout << "leftInorder :";
for (int i = leftInorderBegin; i < leftInorderEnd; i++) {
cout << inorder[i] << " ";
}
cout << endl;
cout << "rightInorder :";
for (int i = rightInorderBegin; i < rightInorderEnd; i++) {
cout << inorder[i] << " ";
}
cout << endl;
cout << "leftPreorder :";
for (int i = leftPreorderBegin; i < leftPreorderEnd; i++) {
cout << preorder[i] << " ";
}
cout << endl;
cout << "rightPreorder :";
for (int i = rightPreorderBegin; i < rightPreorderEnd; i++) {
cout << preorder[i] << " ";
}
cout << endl;
root->left = traversal(inorder, leftInorderBegin, leftInorderEnd, preorder, leftPreorderBegin, leftPreorderEnd);
root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, preorder, rightPreorderBegin, rightPreorderEnd);
return root;
}
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
if (inorder.size() == 0 || preorder.size() == 0) return NULL;
return traversal(inorder, 0, inorder.size(), preorder, 0, preorder.size());
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
- Construct Binary Tree from Preorder and Inorder Traversal, final version, C++ code:
class Solution {
private:
TreeNode* traversal (vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& preorder, int preorderBegin, int preorderEnd) {
if (preorderBegin == preorderEnd) return NULL;
int rootValue = preorder[preorderBegin];
TreeNode* root = new TreeNode(rootValue);
if (preorderEnd - preorderBegin == 1) return root;
int delimiterIndex;
for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {
if (inorder[delimiterIndex] == rootValue) break;
}
// Slice inorder array
int leftInorderBegin = inorderBegin;
int leftInorderEnd = delimiterIndex;
int rightInorderBegin = delimiterIndex + 1;
int rightInorderEnd = inorderEnd;
// Slice preorder array
int leftPreorderBegin = preorderBegin + 1;
int leftPreorderEnd = preorderBegin + 1 + delimiterIndex - inorderBegin;
int rightPreorderBegin = preorderBegin + 1 + (delimiterIndex - inorderBegin);
int rightPreorderEnd = preorderEnd;
root->left = traversal(inorder, leftInorderBegin, leftInorderEnd, preorder, leftPreorderBegin, leftPreorderEnd);
root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, preorder, rightPreorderBegin, rightPreorderEnd);
return root;
}
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
if (inorder.size() == 0 || preorder.size() == 0) return NULL;
// Maintain left-closed right-open intervals
return traversal(inorder, 0, inorder.size(), preorder, 0, preorder.size());
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
# Discussion
Preorder and inorder can uniquely determine a binary tree.
Postorder and inorder can uniquely determine a binary tree.
Can preorder and postorder uniquely determine a binary tree?
Preorder and postorder cannot uniquely determine a binary tree! Without the inorder traversal, we cannot confirm which part is left or right, nor can we properly segment the tree.
Consider an example:
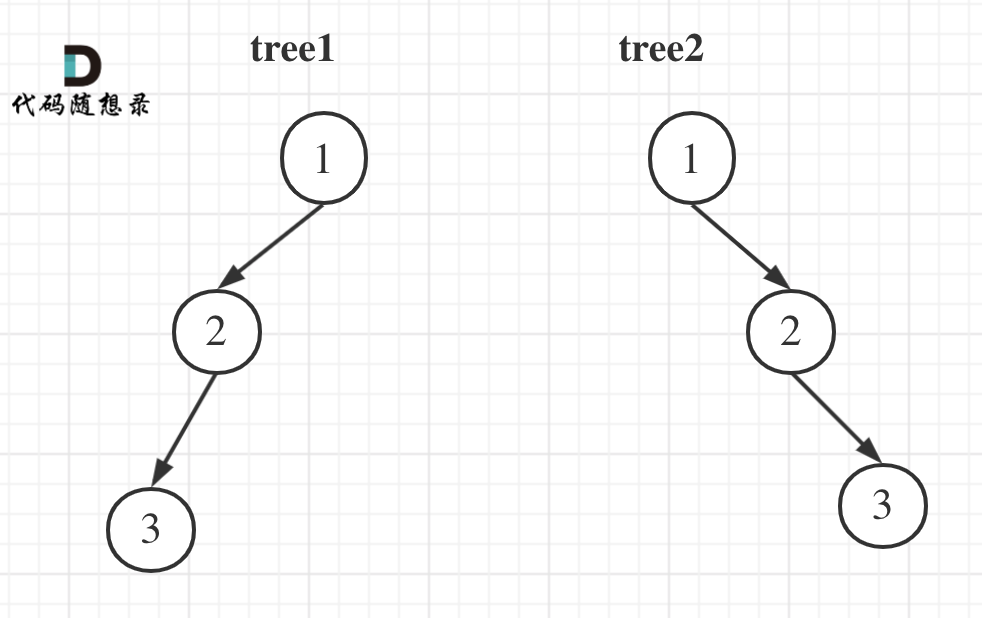
The preorder traversal for tree1 is [1 2 3], and the postorder traversal is [3 2 1].
The preorder traversal for tree2 is [1 2 3], and the postorder traversal is [3 2 1].
So, tree1 and tree2 have identical preorder and postorder traversals. Are they the same tree? Clearly not!
Thus, preorder and postorder cannot uniquely determine a binary tree!
# Summary
Previously, we tackled problems related to traversing binary trees. Now, we begin constructing them. While the logic is simple, implementing the code isn't trivial.
Avoid becoming presumptuous—ground yourself to code it out.
I provided versions with and without debug logs because such problems rarely result in correct implementation without testing, and one should verify execution against expectations rather than relying solely on mental simulations.
Finally, I elaborated on why preorder and inorder can uniquely determine a binary tree, postorder and inorder likewise—but preorder and postorder cannot.
Study well to achieve clarity in binary tree construction algorithms.
