Theoretical Foundation of Backtracking Algorithm

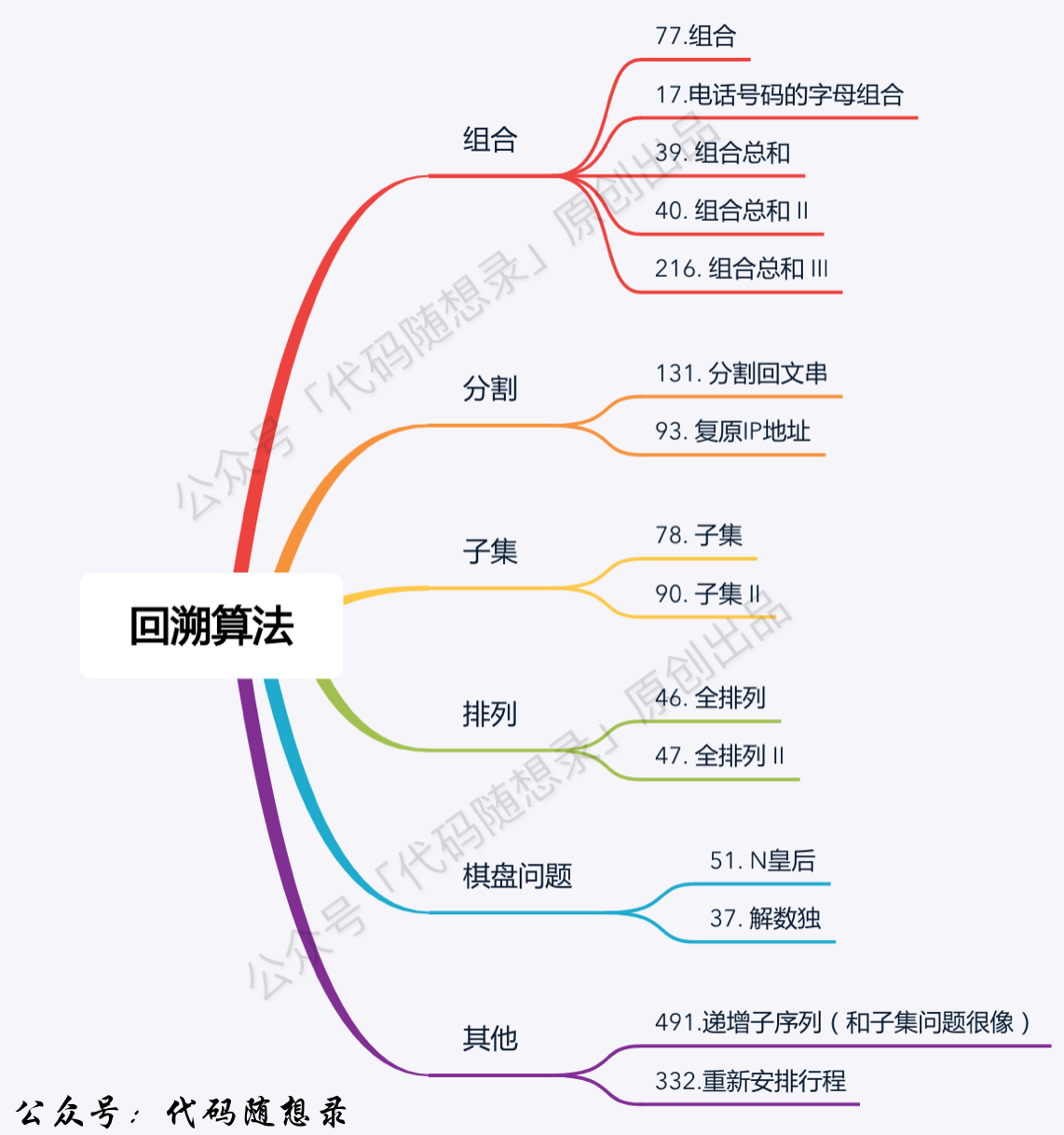
Problem Classification

Theoretical Foundation

What is Backtracking

The backtracking method can also be referred to as the backtracking search method. It is a way of searching.

In the binary tree series, we have mentioned backtracking multiple times, such as in Binary Tree Traversal with Recursion and Backtracking (opens new window).

Backtracking is a byproduct of recursion. Whenever there is recursion, there will be backtracking.

Therefore, in the following explanations, the backtracking function and the recursive function refer to the same function.

Efficiency of Backtracking

How efficient is the backtracking method? I want to make it clear that although backtracking is difficult and not easy to understand, it is not a high-efficiency algorithm.

Because the essence of backtracking is exhaustive search, trying all possibilities and then selecting the desired answer. If you want to make the backtracking method more efficient, you can add some pruning operations, but it cannot change the fact that backtracking is exhaustive.

Then why use backtracking if it is not efficient?

Because there's no better option. For some problems, getting a brute-force solution is already quite good, and at most, you can prune it a bit. There isn’t a more efficient solution.

At this point, you might be wondering, what kind of problems are so intriguing that they can only be solved by brute-force search?

Problems Solved by Backtracking

Backtracking can generally solve the following types of problems:

• Combination Problems: Finding sets of k numbers from a total of N numbers based on certain rules.
• Partition Problems: Determining the number of ways to partition a string according to some rules.
• Subset Problems: Identifying how many subsets of a set of N numbers meet certain conditions.
• Permutation Problems: Determining the number of arrangements in which N numbers can be organized according to certain rules.
• Board Problems: Solving problems like N-Queens, Sudoku, etc.

You will notice that each of these problems is quite complex!

Additionally, some people might not distinguish between combinations and permutations.

Combination does not emphasize the order of elements, while permutation does.

For example: in combination, {1, 2} and {2, 1} are considered the same set, because the order doesn’t matter. But in permutation, {1, 2} and {2, 1} are considered two different sets.

Just remember: combination is unordered, permutation is ordered.

Understanding Backtracking

Problems solved by backtracking can all be abstracted into a tree structure. Yes, I mean that all backtracking problems can be represented as a tree structure!

Because backtracking generally involves recursively searching for subsets within a set, the size of the set forms the width of the tree, and the depth of the recursion forms the depth of the tree.

Recursion must have a termination condition, so it is inherently a tree with limited height (N-ary tree).

Beginners might not fully understand this yet. In the subsequent explanations of problems solved by backtracking, I will emphasize this point and provide corresponding examples with diagrams. For now, having this concept in mind is enough.

Backtracking Template

Here is the backtracking algorithm template as summarized by Carl.

When discussing Binary Tree Recursive Traversal (opens new window), we talked about the three steps of recursion. Here, I will introduce the three steps of backtracking.

Backtracking Function Template: Return Value and Parameters

In the backtracking algorithm, my habit is to name the function backtracking. Everyone can choose their own naming conventions.

In the backtracking algorithm, the function typically returns void.

Now, let's look at the parameters, because determining what parameters are needed for backtracking is not as easy as it is for binary tree recursion. Usually, you define the logic first and fill in whatever parameters are needed.

For the subsequent explanation of backtracking problems, to aid understanding, I will define the parameters from the beginning.

The pseudocode for the backtracking function is as follows:

void backtracking(parameters)

Termination Condition for the Backtracking Function

Since it follows a tree structure, as mentioned when discussing Binary Tree Recursive Traversal (opens new window), there must be a termination condition for traversing a tree structure.

Therefore, backtracking must also have a termination condition.

When the termination condition is met — generally, when you reach a leaf node — it means you found one valid solution, which is stored, and then you end the current level of recursion.

The termination condition pseudocode for a backtracking function is as follows:

if (termination condition) {
    store result;
    return;
}

Process of Backtracking Search

As mentioned before, backtracking is generally about recursively searching within a set, where the size of the set determines the width of the tree, and the recursion depth determines the depth of the tree.

Diagram:

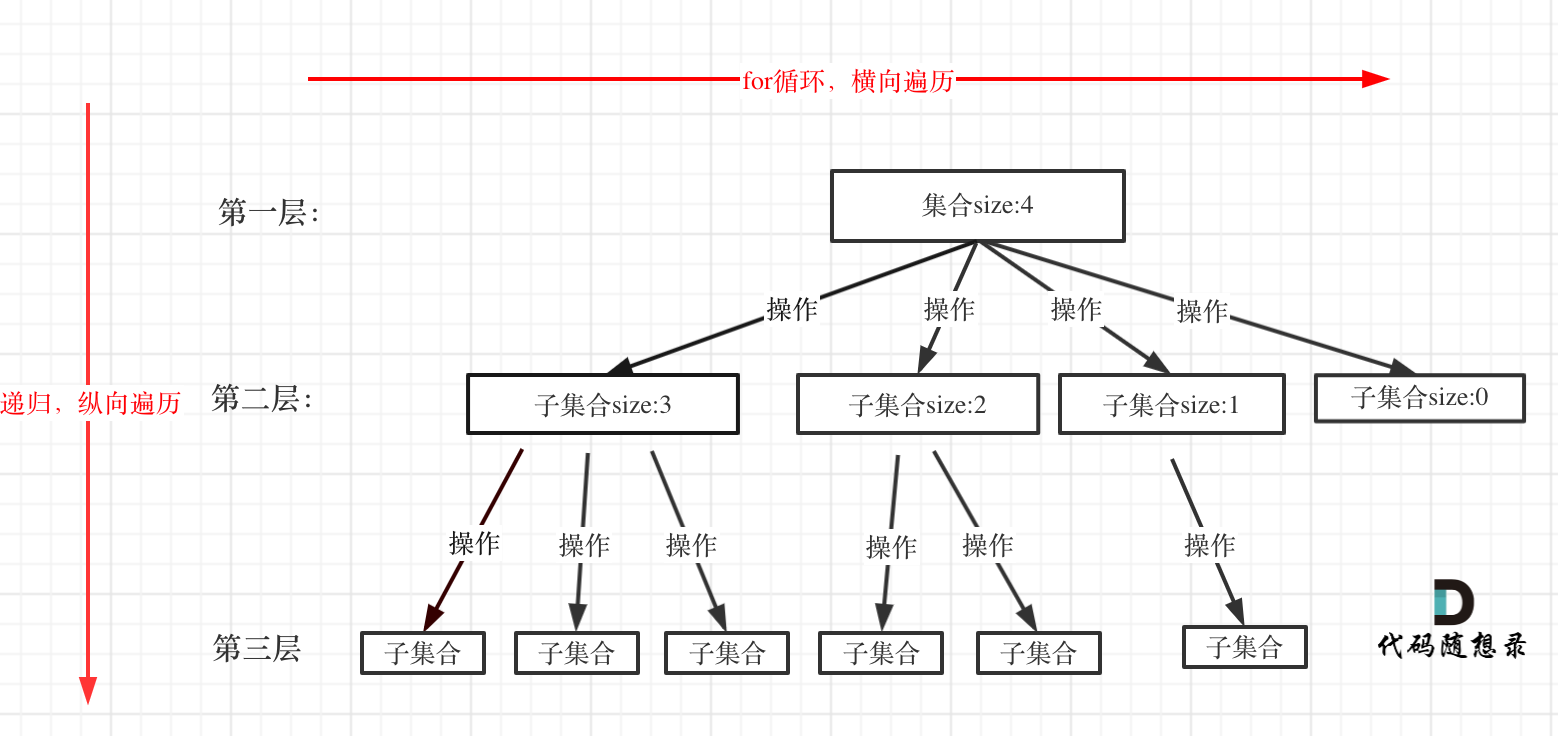
Note in the diagram that I specifically exemplify that the size of the set equals the number of child nodes!

The pseudocode for the backtracking process is as follows:

for (choice: elements in the current level set (the number of child nodes in the tree is the size of the set)) {
    process node;
    backtracking(path, choice list); // Recursion
    backtrack, undo the processed result
}

The for loop is essentially traversing a range of the set, representing how many children a node has, thus executing the loop that many times.

backtracking calls itself, thereby achieving recursion.

From the diagram, you can see that the for loop can be perceived as horizontal traversal, while backtracking (recursion) is vertical traversal. This way, the entire tree is traversed, and generally, searching a leaf node provides one possible result.

After analyzing the process, the framework of the backtracking algorithm template is as follows:

void backtracking(parameters) {
    if (termination condition) {
        store result;
        return;
    }

    for (choice: elements in the current level set (the number of child nodes in the tree is the size of the set)) {
        process node;
        backtracking(path, choice list); // Recursion
        backtrack, undo the processed result
    }
}

This template is very important and will be used for all problems solved by backtracking that follow!

If you have never studied backtracking before, you might feel a bit confused; this is normal. As we integrate with specific problems later, it will become clearer. Those who have practiced backtracking problems should find this quite relatable.

Conclusion

In this article, we discussed what backtracking is and understood that backtracking and recursion complement each other.

We also mentioned the efficiency of backtracking. Essentially, backtracking is a brute-force search method and is not a high-efficiency algorithm.

Then, we listed various types of problems that can be solved using backtracking, noticing that each type is quite complex.

Finally, we noted that problems solved by backtracking can be abstracted as tree structures (N-ary trees) and provided the backtracking algorithm template.

Today is the first day of learning the backtracking algorithm. According to tradition, Carl always begins with an overview, then proceeds with specific problems. It’s normal for newcomers to find it a bit confusing initially; it will be better integrated with specific problems later on.