# 617. Merge Two Binary Trees
LeetCode Problem Link (opens new window)
Given two binary trees, imagine that when you overlay one on top of the other, some nodes of the two binary trees overlap.
You need to merge them into a new binary tree. The merge rule is that if two nodes overlap, then sum node values up as the new value of the merged node. Otherwise, the non-null node will be used as the node of the new tree.
Example 1:
Note: The merge process must start from the root nodes of both trees.
# Approach
I believe the main confusion with this problem is how to traverse two binary trees simultaneously.
Actually, it is the same logic as traversing one tree, just by passing two nodes together and operating on them.
# Recursion
When using recursion on a binary tree, which traversal order should we use?
Any traversal order (pre-order, in-order, or post-order) will work for this problem!
Let's take pre-order traversal as an example.
Animation as shown:
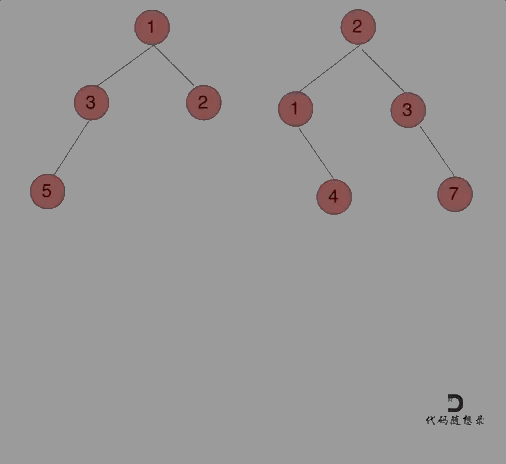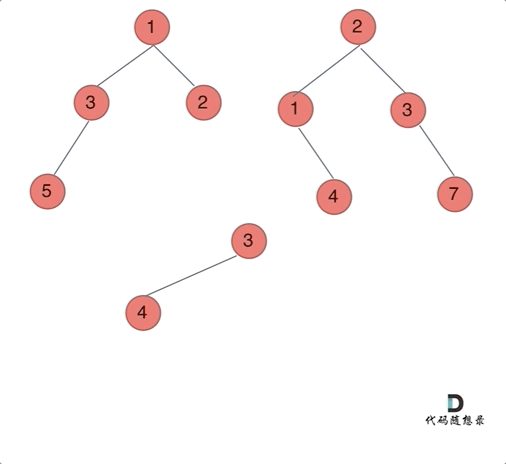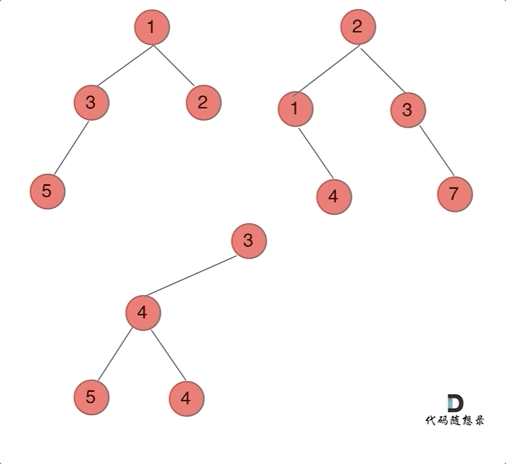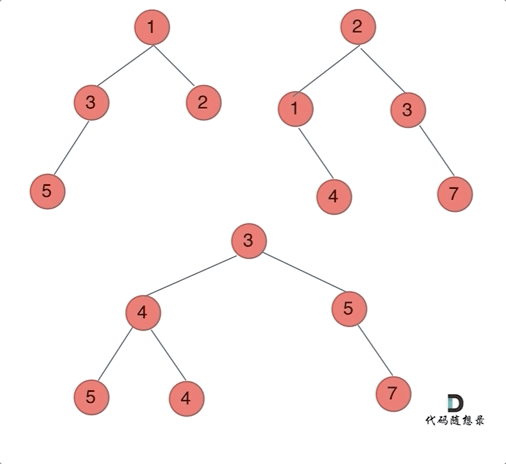
Now let’s solve it using the three-step recursive strategy:
- Determine the parameters and return value of the recursive function:
To merge two binary trees, we need to pass at least the root nodes of both trees as parameters. The return value should be the root node of the merged tree.
The code is as follows:
TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
1
- Set the termination condition:
Since we are dealing with two trees, we have two nodes, t1 and t2. If t1 is NULL, the merged tree should be t2 (it's okay if t2 is also NULL; the merged result will be NULL).
Conversely, if t2 is NULL, the merged tree should be t1 (it's okay if t1 is also NULL; the merged result will be NULL).
The code is as follows:
if (t1 == NULL) return t2; // If t1 is null, the merged result should be t2
if (t2 == NULL) return t1; // If t2 is null, the merged result should be t1
1
2
2
- Define the single-layer recursive logic:
The single-layer logic is straightforward. We will reuse the t1 tree, with t1 as the root node of the merged tree (modifying the original tree's structure).
In the single recursion level, we should sum the elements of both trees together.
t1->val += t2->val;
1
Then, t1's left subtree should be: the result of merging the left subtrees of t1 and t2.
t1's right subtree should be: the result of merging the right subtrees of t1 and t2.
Ultimately, t1 becomes the root node of the merged tree.
The code is as follows:
t1->left = mergeTrees(t1->left, t2->left);
t1->right = mergeTrees(t1->right, t2->right);
return t1;
1
2
3
2
3
Thus, the complete code for pre-order traversal is as follows:
class Solution {
public:
TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
if (t1 == NULL) return t2; // If t1 is null, the merged result should be t2
if (t2 == NULL) return t1; // If t2 is null, the merged result should be t1
// Modify the values and structure of t1
t1->val += t2->val; // Root
t1->left = mergeTrees(t1->left, t2->left); // Left
t1->right = mergeTrees(t1->right, t2->right); // Right
return t1;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
2
3
4
5
6
7
8
9
10
11
12
The in-order traversal is also applicable, and the code is as follows:
class Solution {
public:
TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
if (t1 == NULL) return t2; // If t1 is null, the merged result should be t2
if (t2 == NULL) return t1; // If t2 is null, the merged result should be t1
// Modify the values and structure of t1
t1->left = mergeTrees(t1->left, t2->left); // Left
t1->val += t2->val; // Root
t1->right = mergeTrees(t1->right, t2->right); // Right
return t1;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
2
3
4
5
6
7
8
9
10
11
12
Post-order traversal is also an option, and the code is as follows:
class Solution {
public:
TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
if (t1 == NULL) return t2; // If t1 is null, the merged result should be t2
if (t2 == NULL) return t1; // If t2 is null, the merged result should be t1
// Modify the values and structure of t1
t1->left = mergeTrees(t1->left, t2->left); // Left
t1->right = mergeTrees(t1->right, t2->right); // Right
t1->val += t2->val; // Root
return t1;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
2
3
4
5
6
7
8
9
10
11
12
However, pre-order traversal is the easiest to understand, and I recommend using it.
There is also a method to define a new tree without modifying the structure of t1 and t2.
For pre-order traversal that does not modify the input trees' structure, the code is as follows:
class Solution {
public:
TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
if (t1 == NULL) return t2;
if (t2 == NULL) return t1;
// Define a new node without modifying the original structure of the two trees
TreeNode* root = new TreeNode(0);
root->val = t1->val + t2->val;
root->left = mergeTrees(t1->left, t2->left);
root->right = mergeTrees(t1->right, t2->right);
return root;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
2
3
4
5
6
7
8
9
10
11
12
13
# Iterative Approach
How can we process two trees simultaneously using an iterative method?
As we've discussed in "0101.Symmetric Tree" (opens new window), when determining symmetry, we used a queue to compare nodes from two trees simultaneously.
In this problem, we also use a queue and simulate level-order traversal. The code is as follows:
class Solution {
public:
TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
if (t1 == NULL) return t2;
if (t2 == NULL) return t1;
queue<TreeNode*> que;
que.push(t1);
que.push(t2);
while(!que.empty()) {
TreeNode* node1 = que.front(); que.pop();
TreeNode* node2 = que.front(); que.pop();
// Both nodes are not null, so sum values
node1->val += node2->val;
// If both trees' left nodes are not null, add to the queue
if (node1->left != NULL && node2->left != NULL) {
que.push(node1->left);
que.push(node2->left);
}
// If both trees' right nodes are not null, add to the queue
if (node1->right != NULL && node2->right != NULL) {
que.push(node1->right);
que.push(node2->right);
}
// Assign node2's left to node1 if node1's left is null
if (node1->left == NULL && node2->left != NULL) {
node1->left = node2->left;
}
// Assign node2's right to node1 if node1's right is null
if (node1->right == NULL && node2->right != NULL) {
node1->right = node2->right;
}
}
return t1;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
# Extension
It's also possible to demonstrate advanced pointer manipulation. Here’s an unconventional approach that I sketched; feel free to look it over, but don't get sidetracked.
In the following code, if you want to change the values of a binary tree, you should pass a pointer to a pointer.
The code below uses pre-order traversal:
class Solution {
public:
void process(TreeNode** t1, TreeNode** t2) {
if ((*t1) == NULL && (*t2) == NULL) return;
if ((*t1) != NULL && (*t2) != NULL) {
(*t1)->val += (*t2)->val;
}
if ((*t1) == NULL && (*t2) != NULL) {
*t1 = *t2;
return;
}
if ((*t1) != NULL && (*t2) == NULL) {
return;
}
process(&((*t1)->left), &((*t2)->left));
process(&((*t1)->right), &((*t2)->right));
}
TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
process(&t1, &t2);
return t1;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# Summary
Merging binary trees is a classic topic in binary tree manipulation. If you haven't encountered it before, it can indeed be challenging since we're used to manipulating a single binary tree. Working with two binary trees simultaneously can be puzzling.
This is not our first time handling two binary trees together. In "0101.Symmetric Tree" (opens new window), we also manipulated two binary trees simultaneously.
In the iterative approach, usually when dealing with two trees, we use a queue to simulate level-order traversal and process nodes from both trees together. This method is the most comprehensible compared to simulating recursion.
In the final extension, I provided a pointer manipulation trick. You can explore it further if you're learning C++.
# Other Language Versions
# Java
class Solution {
// Recursive
public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
if (root1 == null) return root2;
if (root2 == null) return root1;
root1.val += root2.val;
root1.left = mergeTrees(root1.left, root2.left);
root1.right = mergeTrees(root1.right, root2.right);
return root1;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
2
3
4
5
6
7
8
9
10
11
12
class Solution {
// Using Stack Iteratively
public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
if (root1 == null) {
return root2;
}
if (root2 == null) {
return root1;
}
Stack<TreeNode> stack = new Stack<>();
stack.push(root2);
stack.push(root1);
while (!stack.isEmpty()) {
TreeNode node1 = stack.pop();
TreeNode node2 = stack.pop();
node1.val += node2.val;
if (node2.right != null && node1.right != null) {
stack.push(node2.right);
stack.push(node1.right);
} else {
if (node1.right == null) {
node1.right = node2.right;
}
}
if (node2.left != null && node1.left != null) {
stack.push(node2.left);
stack.push(node1.left);
} else {
if (node1.left == null) {
node1.left = node2.left;
}
}
}
return root1;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
// Using Queue Iteratively
public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
if (root1 == null) return root2;
if (root2 == null) return root1;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root1);
queue.offer(root2);
while (!queue.isEmpty()) {
TreeNode node1 = queue.poll();
TreeNode node2 = queue.poll();
// Both nodes must be non-null here, so add values
node1.val = node1.val + node2.val;
// If both trees have non-null left nodes, add them to the queue
if (node1.left != null && node2.left != null) {
queue.offer(node1.left);
queue.offer(node2.left);
}
// If both trees have non-null right nodes, add them to the queue
if (node1.right != null && node2.right != null) {
queue.offer(node1.right);
queue.offer(node2.right);
}
// If node1's left node is null, assign it directly
if (node1.left == null && node2.left != null) {
node1.left = node2.left;
}
// If node1's right node is null, assign it directly
if (node1.right == null && node2.right != null) {
node1.right = node2.right;
}
}
return root1;
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
# Python
(Version One) Recursive - Pre-order - Modifies root1
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def mergeTrees(self, root1: TreeNode, root2: TreeNode) -> TreeNode:
# Base case:
# If any node is null, return the other node directly. If both are null, return None directly.
if not root1:
return root2
if not root2:
return root1
# Known from the above base case that both node1 and node2 are non-null at this point.
root1.val += root2.val # Root
root1.left = self.mergeTrees(root1.left, root2.left) # Left
root1.right = self.mergeTrees(root1.right, root2.right) # Right
return root1 # ⚠️ Note: In this solution, we reuse the given nodes instead of creating new ones, saving time and space.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
(Version Two) Recursive - Pre-order - New root
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def mergeTrees(self, root1: TreeNode, root2: TreeNode) -> TreeNode:
# Base case:
# If any node is null, return the other node directly. If both are null, return None directly.
if not root1:
return root2
if not root2:
return root1
# Known from the above base case that both node1 and node2 are non-null at this point.
root = TreeNode() # Create a new node
root.val += root1.val + root2.val# Root
root.left = self.mergeTrees(root1.left, root2.left) # Left
root.right = self.mergeTrees(root1.right, root2.right) # Right
return root # ⚠️ Note: In this solution, we create new nodes.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
(Version Three) Iterative
class Solution:
def mergeTrees(self, root1: TreeNode, root2: TreeNode) -> TreeNode:
if not root1:
return root2
if not root2:
return root1
queue = deque()
queue.append(root1)
queue.append(root2)
while queue:
node1 = queue.popleft()
node2 = queue.popleft()
# Update queue
# Add to queue only if both nodes have left children
if node1.left and node2.left:
queue.append(node1.left)
queue.append(node2.left)
# Add to queue only if both nodes have right children
if node1.right and node2.right:
queue.append(node1.right)
queue.append(node2.right)
# Update current node, and also change current node's left and right children.
node1.val += node2.val
if not node1.left and node2.left:
node1.left = node2.left
if not node1.right and node2.right:
node1.right = node2.right
return root1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
(Version Four) Iterative + Code Optimization
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
from collections import deque
class Solution:
def mergeTrees(self, root1: TreeNode, root2: TreeNode) -> TreeNode:
if not root1:
return root2
if not root2:
return root1
queue = deque()
queue.append((root1, root2))
while queue:
node1, node2 = queue.popleft()
node1.val += node2.val
if node1.left and node2.left:
queue.append((node1.left, node2.left))
elif not node1.left:
node1.left = node2.left
if node1.right and node2.right:
queue.append((node1.right, node2.right))
elif not node1.right:
node1.right = node2.right
return root1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# Go
// Pre-order traversal
func mergeTrees(root1 *TreeNode, root2 *TreeNode) *TreeNode {
if root1 == nil {
return root2
}
if root2 == nil {
return root1
}
root1.Val += root2.Val
root1.Left = mergeTrees(root1.Left, root2.Left)
root1.Right = mergeTrees(root1.Right, root2.Right)
return root1
}
// Iterative version
func mergeTrees(root1 *TreeNode, root2 *TreeNode) *TreeNode {
queue := make([]*TreeNode,0)
if root1 == nil{
return root2
}
if root2 == nil{
return root1
}
queue = append(queue,root1)
queue = append(queue,root2)
for size := len(queue); size>0; size=len(queue) {
node1 := queue[0]
queue = queue[1:]
node2 := queue[0]
queue = queue[1:]
node1.Val += node2.Val
// Left child nodes are non-null
if node1.Left != nil && node2.Left != nil {
queue = append(queue,node1.Left)
queue = append(queue,node2.Left)
}
// Right child nodes are non-null
if node1.Right !=nil && node2.Right !=nil {
queue = append(queue, node1.Right)
queue = append(queue, node2.Right)
}
// If tree 1's left child is nil, directly assign tree 2's left child
if node1.Left == nil {
node1.Left = node2.Left
}
// If tree 1's right child is nil, directly assign tree 2's right child
if node1.Right == nil {
node1.Right = node2.Right
}
}
return root1
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
# JavaScript
Recursive Method:
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root1
* @param {TreeNode} root2
* @return {TreeNode}
*/
var mergeTrees = function (root1, root2) {
const preOrder = (root1, root2) => {
if (!root1)
return root2
if (!root2)
return root1;
root1.val += root2.val;
root1.left = preOrder(root1.left, root2.left);
root1.right = preOrder(root1.right, root2.right);
return root1;
}
return preOrder(root1, root2);
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
Iterative Method:
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root1
* @param {TreeNode} root2
* @return {TreeNode}
*/
var mergeTrees = function(root1, root2) {
if (root1 === null) return root2;
if (root2 === null) return root1;
let queue = [];
queue.push(root1);
queue.push(root2);
while (queue.length) {
let node1 = queue.shift();
let node2 = queue.shift();;
node1.val += node2.val;
if (node1.left !== null && node2.left !== null) {
queue.push(node1.left);
queue.push(node2.left);
}
if (node1.right !== null && node2.right !== null) {
queue.push(node1.right);
queue.push(node2.right);
}
if (node1.left === null && node2.left !== null) {
node1.left = node2.left;
}
if (node1.right === null && node2.right !== null) {
node1.right = node2.right;
}
}
return root1;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
# TypeScript
Recursive Method:
function mergeTrees(root1: TreeNode | null, root2: TreeNode | null): TreeNode | null {
if (root1 === null) return root2;
if (root2 === null) return root1;
const resNode: TreeNode = new TreeNode(root1.val + root2.val);
resNode.left = mergeTrees(root1.left, root2.left);
resNode.right = mergeTrees(root1.right, root2.right);
return resNode;
};
1
2
3
4
5
6
7
8
2
3
4
5
6
7
8
Iterative Method:
function mergeTrees(root1: TreeNode | null, root2: TreeNode | null): TreeNode | null {
if (root1 === null) return root2;
if (root2 === null) return root1;
const helperQueue1: TreeNode[] = [],
helperQueue2: TreeNode[] = [];
helperQueue1.push(root1);
helperQueue2.push(root2);
let tempNode1: TreeNode,
tempNode2: TreeNode;
while (helperQueue1.length > 0) {
tempNode1 = helperQueue1.shift()!;
tempNode2 = helperQueue2.shift()!;
tempNode1.val += tempNode2.val;
if (tempNode1.left !== null && tempNode2.left !== null) {
helperQueue1.push(tempNode1.left);
helperQueue2.push(tempNode2.left);
} else if (tempNode1.left === null) {
tempNode1.left = tempNode2.left;
}
if (tempNode1.right !== null && tempNode2.right !== null) {
helperQueue1.push(tempNode1.right);
helperQueue2.push(tempNode2.right);
} else if (tempNode1.right === null) {
tempNode1.right = tempNode2.right;
}
}
return root1;
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# Scala
Recursive:
object Solution {
def mergeTrees(root1: TreeNode, root2: TreeNode): TreeNode = {
if (root1 == null) return root2 // If root1 is null, return root2
if (root2 == null) return root1 // If root2 is null, return root1
// Create a new node with the sum value of the two nodes
var node = new TreeNode(root1.value + root2.value)
// Recurse downwards
node.left = mergeTrees(root1.left, root2.left)
node.right = mergeTrees(root1.right, root2.right)
node // Return node, the return keyword can be omitted
}
}
1
2
3
4
5
6
7
8
9
10
11
12
2
3
4
5
6
7
8
9
10
11
12
Iterative:
object Solution {
import scala.collection.mutable
def mergeTrees(root1: TreeNode, root2: TreeNode): TreeNode = {
if (root1 == null) return root2
if (root2 == null) return root1
var stack = mutable.Stack[TreeNode]()
// Push node2 first, then node1
stack.push(root2)
stack.push(root1)
while (!stack.isEmpty) {
var node1 = stack.pop()
var node2 = stack.pop()
node1.value += node2.value
if (node1.left != null && node2.left != null) {
stack.push(node2.left)
stack.push(node1.left)
} else {
if(node1.left == null){
node1.left = node2.left
}
}
if (node1.right != null && node2.right != null) {
stack.push(node2.right)
stack.push(node1.right)
} else {
if(node1.right == null){
node1.right = node2.right
}
}
}
root1
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# Rust
Recursive:
use std::cell::RefCell;
use std::rc::Rc;
impl Solution {
pub fn merge_trees(
root1: Option<Rc<RefCell<TreeNode>>>,
root2: Option<Rc<RefCell<TreeNode>>>,
) -> Option<Rc<RefCell<TreeNode>>> {
if root1.is_none() {
return root2;
}
if root2.is_none() {
return root1;
}
let binding = root1.clone();
let mut node1 = binding.as_ref().unwrap().borrow_mut();
let node2 = root2.as_ref().unwrap().borrow_mut();
node1.left = Self::merge_trees(node1.left.clone(), node2.left.clone());
node1.right = Self::merge_trees(node1.right.clone(), node2.right.clone());
node1.val += node2.val;
root1
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Iterative:
impl Solution {
pub fn merge_trees(
root1: Option<Rc<RefCell<TreeNode>>>,
root2: Option<Rc<RefCell<TreeNode>>>,
) -> Option<Rc<RefCell<TreeNode>>> {
if root1.is_none() {
return root2;
}
if root2.is_none() {
return root1;
}
let mut stack = vec![];
stack.push(root2);
stack.push(root1.clone());
while !stack.is_empty() {
let node1 = stack.pop().unwrap().unwrap();
let node2 = stack.pop().unwrap().unwrap();
let mut node1 = node1.borrow_mut();
let node2 = node2.borrow();
node1.val += node2.val;
if node1.left.is_some() && node2.left.is_some() {
stack.push(node2.left.clone());
stack.push(node1.left.clone());
}
if node1.right.is_some() && node2.right.is_some() {
stack.push(node2.right.clone());
stack.push(node1.right.clone());
}
if node1.left.is_none() && node2.left.is_some() {
node1.left = node2.left.clone();
}
if node1.right.is_none() && node2.right.is_some() {
node1.right = node2.right.clone();
}
}
root1
}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
# C#
public TreeNode MergeTrees(TreeNode root1, TreeNode root2)
{
if (root1 == null) return root2;
if (root2 == null) return root1;
root1.val += root2.val;
root1.left = MergeTrees(root1.left, root2.left);
root1.right = MergeTrees(root1.right, root2.right);
return root1;
}
1
2
3
4
5
6
7
8
9
10
11
2
3
4
5
6
7
8
9
10
11
Copyright © 2025 keetcoder