# 101. Symmetric Tree
LeetCode Problem Link (opens new window)
Given a binary tree, check whether it is a mirror of itself (i.e., symmetric around its center).

# Approach
First, think clearly about which two nodes we are comparing to determine whether the binary tree is symmetric. It's not just the left and right nodes!
To determine whether a binary tree is symmetric, we should compare whether the left subtree and the right subtree of the root node are mirror images of each other. Once you understand this, you'll realize that we are actually comparing two trees (the left and right subtrees of the root node). Thus, during the recursive traversal, we should also traverse two trees simultaneously.
So, how should we compare them?
We compare whether the inner and outer elements of the two subtrees are equal, as illustrated in the diagram:
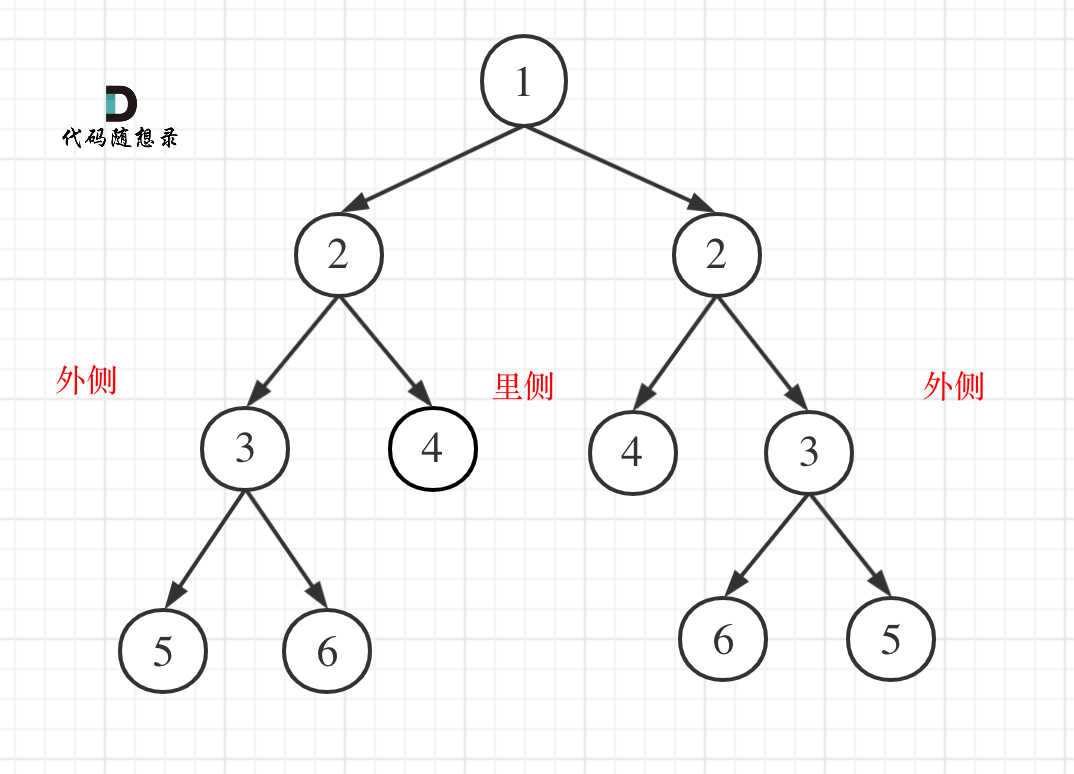
What should the traversal order be?
The traversal order should be "post-order" because we need to use the return values of the recursive function to determine whether the inner and outer nodes of the two subtrees are equal.
Because we are traversing two trees and comparing the inner and outer nodes, the exact traversal order is left-right-root for one tree and right-left-root for the other.
This can still be considered as post-order traversal, although it's not a strict post-order traversal on a single tree.
In fact, post-order can be seen as a form of backtracking, which will be discussed in detail when we talk about backtracking.
Now, let's write the recursive solution.
# Recursive Approach
Recursive solution involves three steps:
- Determine the parameters and return value of the recursive function.
We need to compare the left and right subtrees of the root node to see if they are mirror images of each other. Naturally, the parameters should include the left and right subtree nodes.
The return type should be bool.
Code:
bool compare(TreeNode* left, TreeNode* right)
- Determine the termination condition.
First, handle cases where nodes might be null. Otherwise, we risk accessing null pointers when comparing node values later.
Possible null scenarios are:
- Left node is null, right node is not null, not symmetric, return false.
- Left node is not null, right node is null, not symmetric, return false.
- Both are null, symmetric, return true.
At this point, we've handled cases where nodes are null. The remaining cases are where both nodes are not null:
- Both are not null; compare their values. If they are not the same, return false.
Code:
if (left == NULL && right != NULL) return false;
else if (left != NULL && right == NULL) return false;
else if (left == NULL && right == NULL) return true;
else if (left->val != right->val) return false; // Note no else statement here
2
3
4
Note that in the last condition, I didn't use an else, but an else if. Once we've eliminated all other possibilities, we're left with the case where both nodes are not null and have equal values.
- Determine the logic for a single recursive layer.
Now we handle the case where both nodes are not null and have equal values.
- Compare the outer sides of the subtrees: pass in the left child of the left node and the right child of the right node.
- Compare the inner sides: pass in the right child of the left node and the left child of the right node.
- If both sides are symmetric, return true; if one side is not, return false.
Code:
bool outside = compare(left->left, right->right); // Left subtree: left, Right subtree: right
bool inside = compare(left->right, right->left); // Left subtree: right, Right subtree: left
bool isSame = outside && inside; // Left subtree: root, Right subtree: root (logical processing)
return isSame;
2
3
4
In the above code, the traversal order for one tree is left-right-root, and for the other is right-left-root. Therefore, I consider this traversal to be "post-order" (though not strictly post-order on a single tree).
Here is the complete C++ recursive solution:
class Solution {
public:
bool compare(TreeNode* left, TreeNode* right) {
// First, eliminate the null node scenarios
if (left == NULL && right != NULL) return false;
else if (left != NULL && right == NULL) return false;
else if (left == NULL && right == NULL) return true;
// Eliminate null nodes, then eliminate cases where values are not equal
else if (left->val != right->val) return false;
// At this point, both nodes are non-null and values are equal
// Now perform recursion to check the next layer
bool outside = compare(left->left, right->right); // Left subtree: left, Right subtree: right
bool inside = compare(left->right, right->left); // Left subtree: right, Right subtree: left
bool isSame = outside && inside; // Left subtree: root, Right subtree: root (logical processing)
return isSame;
}
bool isSymmetric(TreeNode* root) {
if (root == NULL) return true;
return compare(root->left, root->right);
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
I’ve provided a detailed code that might not be the most concise, but it clearly lays out each step and thought process.
If you look at concise code snippets on the internet without this explanation, they might seem simple but hide a lot of logical deductions. The result of blindly copying without understanding is that you pass a "simple problem" without truly comprehending its logic.
Of course, you can refine the code as follows:
class Solution {
public:
bool compare(TreeNode* left, TreeNode* right) {
if (left == NULL && right != NULL) return false;
else if (left != NULL && right == NULL) return false;
else if (left == NULL && right == NULL) return true;
else if (left->val != right->val) return false;
else return compare(left->left, right->right) && compare(left->right, right->left);
}
bool isSymmetric(TreeNode* root) {
if (root == NULL) return true;
return compare(root->left, root->right);
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
This code is quite concise but misses out on many logical details and does not clearly reflect the recursive solution.
Thus, when solving problems, ensure you understand the logic clearly and thoroughly. Code every scenario, and only then pursue more concise code.
# Iterative Approach
This problem can also be solved using an iterative approach. However, note that the iterative approach here isn't a typical pre-order, in-order, or post-order traversal because this problem's essence is about two trees being mirror images of each other, which doesn't coincide with conventional traversal orders.
Here, we can use a queue to compare whether the two trees (the left and right subtrees of the root) are mirror images, not a level order traversal.
# Using a Queue
A queue can be used to ascertain the symmetry between the left and right subtrees of the root node. This is shown in the animation:
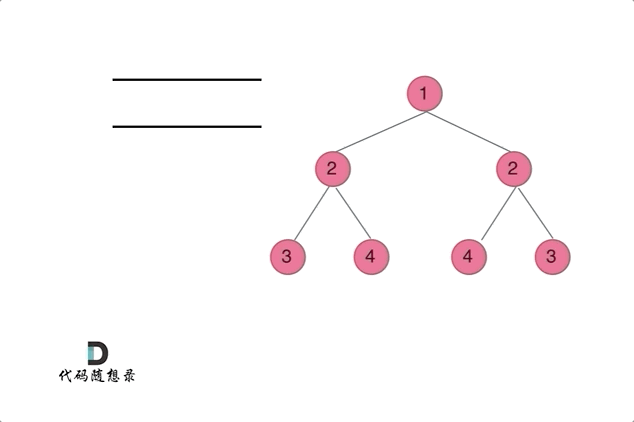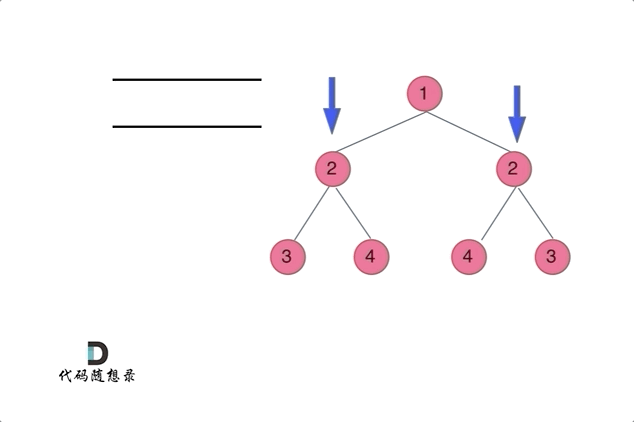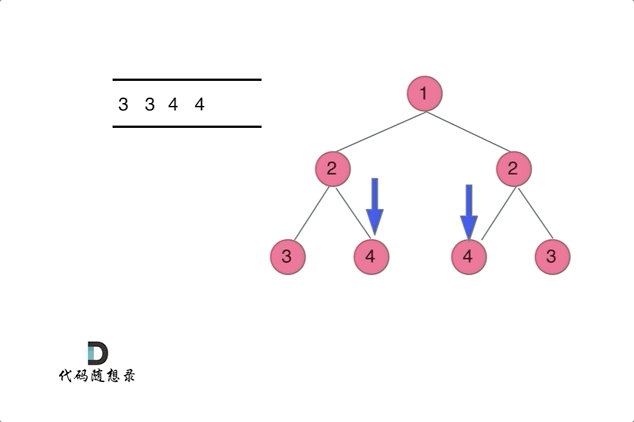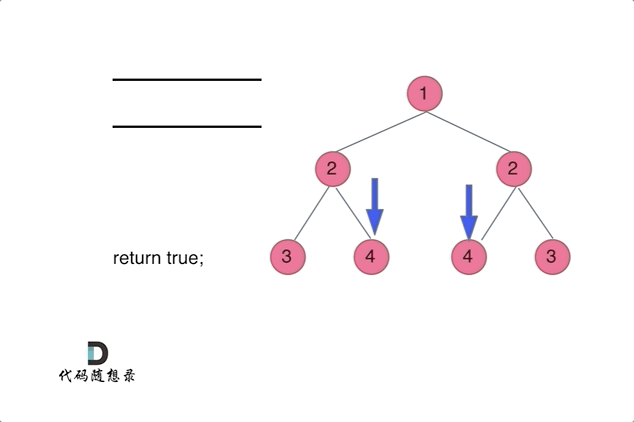
Check for similar conditions as with the recursive approach:
class Solution {
public:
bool isSymmetric(TreeNode* root) {
if (root == NULL) return true;
queue<TreeNode*> que;
que.push(root.left); // Add the head of the left subtree to the queue
que.push(root.right); // Add the head of the right subtree to the queue
while (!que.empty()) { // Now, check if these two trees are mirror images
TreeNode* leftNode = que.front(); que.pop();
TreeNode* rightNode = que.front(); que.pop();
if (!leftNode && !rightNode) { // Both nodes are null, so symmetric
continue;
}
// Either one node is null, or both are non-null but with different values
if ((!leftNode || !rightNode || (leftNode->val != rightNode->val))) {
return false;
}
que.push(leftNode->left); // Add left child's left
que.push(rightNode->right); // Add right child's right
que.push(leftNode->right); // Add left child's right
que.push(rightNode->left); // Add right child's left
}
return true;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# Using a Stack
Observant readers might notice that the iterative approach essentially arranges the nodes that need to be compared into a container, which you then compare in pairs. Thus, a stack can also be used.
Just change the queue to a stack, and the rest remains the same. Here is the code:
class Solution {
public:
bool isSymmetric(TreeNode* root) {
if (root == NULL) return true;
stack<TreeNode*> st;
st.push(root.left);
st.push(root.right);
while (!st.empty()) {
TreeNode* rightNode = st.top(); st.pop();
TreeNode* leftNode = st.top(); st.pop();
if (!leftNode && !rightNode) {
continue;
}
if ((!leftNode || !rightNode || (leftNode->val != rightNode->val))) {
return false;
}
st.push(leftNode->left);
st.push(rightNode->right);
st.push(leftNode->right);
st.push(rightNode->left);
}
return true;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# Summary
In this deep-dive analysis of a "simple" binary tree problem, you might find that thoroughly understanding a problem isn’t that simple. There is still a difference between reaching acceptance on LeetCode and truly mastering the problem.
We've covered both recursive and iterative methods. Again, the recursive approach is tackled using three definitive steps. If you only look at the streamlined code, you wouldn't see how these three steps solve the problem at all.
For the iterative method, we used a queue. Note that this isn't a level-order traversal but merely a way to pair the elements for comparison. Understanding this essence, you'll see that queues, stacks, or even arrays could work.
For those who have attempted this problem before, revisit it after reading this explanation, and you'll find new insights!
# Related Problem Recommendations
These problems are essentially the same as this one and can be solved with slight modifications:
# Versions in Other Languages
# Java:
/**
* Recursive Approach
*/
public boolean isSymmetric1(TreeNode root) {
return compare(root.left, root.right);
}
private boolean compare(TreeNode left, TreeNode right) {
if (left == null && right != null) {
return false;
}
if (left != null && right == null) {
return false;
}
if (left == null && right == null) {
return true;
}
if (left.val != right.val) {
return false;
}
// Compare outer side
boolean compareOutside = compare(left.left, right.right);
// Compare inner side
boolean compareInside = compare(left.right, right.left);
return compareOutside && compareInside;
}
/**
* Iterative Approach
* Using a double-ended queue, akin to two stacks
*/
public boolean isSymmetric2(TreeNode root) {
Deque<TreeNode> deque = new LinkedList<>();
deque.offerFirst(root.left);
deque.offerLast(root.right);
while (!deque.isEmpty()) {
TreeNode leftNode = deque.pollFirst();
TreeNode rightNode = deque.pollLast();
if (leftNode == null && rightNode == null) {
continue;
}
if (leftNode == null || rightNode == null || leftNode.val != rightNode.val) {
return false;
}
deque.offerFirst(leftNode.left);
deque.offerFirst(leftNode.right);
deque.offerLast(rightNode.right);
deque.offerLast(rightNode.left);
}
return true;
}
/**
* Iterative Approach
* Using a standard queue
*/
public boolean isSymmetric3(TreeNode root) {
Queue<TreeNode> deque = new LinkedList<>();
deque.offer(root.left);
deque.offer(root.right);
while (!deque.isEmpty()) {
TreeNode leftNode = deque.poll();
TreeNode rightNode = deque.poll();
if (leftNode == null && rightNode == null) {
continue;
}
if (leftNode == null || rightNode == null || leftNode.val != rightNode.val) {
return false;
}
// Here, the order is different from using Deque
deque.offer(leftNode.left);
deque.offer(rightNode.right);
deque.offer(leftNode.right);
deque.offer(rightNode.left);
}
return true;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
# Python:
Recursive Approach:
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
if not root:
return True
return self.compare(root.left, root.right)
def compare(self, left, right):
# First eliminate null nodes
if left == None and right != None: return False
elif left != None and right == None: return False
elif left == None and right == None: return True
elif left.val != right.val: return False
# Now handle the case for non-null and equal values
outside = self.compare(left.left, right.right) # Left subtree: left, Right subtree: right
inside = self.compare(left.right, right.left) # Left subtree: right, Right subtree: left
isSame = outside and inside
return isSame
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Iterative Approach: Using Queue
import collections
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
if not root:
return True
queue = collections.deque()
queue.append(root.left)
queue.append(root.right)
while queue:
leftNode = queue.popleft()
rightNode = queue.popleft()
if not leftNode and not rightNode:
continue
if not leftNode or not rightNode or leftNode.val != rightNode.val:
return False
queue.append(leftNode.left)
queue.append(rightNode.right)
queue.append(leftNode.right)
queue.append(rightNode.left)
return True
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
Iterative Approach: Using Stack
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
if not root:
return True
st = [] # Using stack
st.append(root.left)
st.append(root.right)
while st:
rightNode = st.pop()
leftNode=st.pop()
if not leftNode and not rightNode:
continue
if not leftNode or not rightNode or leftNode.val != rightNode.val:
return False
st.append(leftNode.left)
st.append(rightNode.right)
st.append(leftNode.right)
st.append(rightNode.left)
return True
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Level-order Traversal
class Solution:
def isSymmetric(self, root: TreeNode) -> bool:
if not root:
return True
queue = collections.deque([root.left, root.right])
while queue:
level_size = len(queue)
if level_size % 2 != 0:
return False
level_vals = []
for i in range(level_size):
node = queue.popleft()
if node:
level_vals.append(node.val)
queue.append(node.left)
queue.append(node.right)
else:
level_vals.append(None)
if level_vals != level_vals[::-1]:
return False
return True
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# Go:
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
// Recursive
func defs(left *TreeNode, right *TreeNode) bool {
if left == nil && right == nil {
return true;
};
if left == nil || right == nil {
return false;
};
if left.Val != right.Val {
return false;
}
return defs(left.Left, right.Right) && defs(right.Left, left.Right);
}
func isSymmetric(root *TreeNode) bool {
return defs(root.Left, root.Right);
}
// Iterative
func isSymmetric(root *TreeNode) bool {
var queue []*TreeNode;
if root != nil {
queue = append(queue, root.Left, root.Right);
}
for len(queue) > 0 {
left := queue[0];
right := queue[1];
queue = queue[2:];
if left == nil && right == nil {
continue;
}
if left == nil || right == nil || left.Val != right.Val {
return false;
};
queue = append(queue, left.Left, right.Right, right.Left, left.Right);
}
return true;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
# JavaScript:
Recursive check for symmetric binary tree:
var isSymmetric = function(root) {
// Recursive traversal of left and right subtrees; three steps of recursion
// 1. Identify the parameters root.left, root.right and return values true, false
const compareNode = function(left, right) {
// 2. Define the termination condition for null cases
if(left === null && right !== null || left !== null && right === null) {
return false;
} else if(left === null && right === null) {
return true;
} else if(left.val !== right.val) {
return false;
}
// 3. Determine the single-layer recursive logic
let outSide = compareNode(left.left, right.right);
let inSide = compareNode(left.right, right.left);
return outSide && inSide;
}
if(root === null) {
return true;
}
return compareNode(root.left, root.right);
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Queue-based iterative check for symmetric binary tree:
var isSymmetric = function(root) {
// Iterative method to check for symmetric binary tree
// Initially, check if root is null
if(root === null) {
return true;
}
let queue = [];
queue.push(root.left);
queue.push(root.right);
while(queue.length) {
let leftNode = queue.shift(); // Left node
let rightNode = queue.shift(); // Right node
if(leftNode === null && rightNode === null) {
continue;
}
if(leftNode === null || rightNode === null || leftNode.val !== rightNode.val) {
return false;
}
queue.push(leftNode.left); // Left node's left child
queue.push(rightNode.right); // Right node's right child
queue.push(leftNode.right); // Left node's right child
queue.push(rightNode.left); // Right node's left child
}
return true;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
Stack-based iterative check for symmetric binary tree:
var isSymmetric = function(root) {
// Iterative method to check for symmetric binary tree
// Initially, check if root is null
if(root === null) {
return true;
}
let stack = [];
stack.push(root.left);
stack.push(root.right);
while(stack.length) {
let rightNode = stack.pop(); // Left node
let leftNode=stack.pop(); // Right node
if(leftNode === null && rightNode === null) {
continue;
}
if(leftNode === null || rightNode === null || leftNode.val !== rightNode.val) {
return false;
}
stack.push(leftNode.left); // Left node's left child
stack.push(rightNode.right); // Right node's right child
stack.push(leftNode.right); // Left node's right child
stack.push(rightNode.left); // Right node's left child
}
return true;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# TypeScript:
Recursive Method
function isSymmetric(root: TreeNode | null): boolean {
function recur(node1: TreeNode | null, node2: TreeNode | null): boolean {
if (node1 === null && node2 === null) return true;
if (node1 === null || node2 === null) return false;
if (node1.val !== node2.val) return false
let isSym1: boolean = recur(node1.left, node2.right);
let isSym2: boolean = recur(node1.right, node2.left);
return isSym1 && isSym2
}
if (root === null) return true;
return recur(root.left, root.right);
};
2
3
4
5
6
7
8
9
10
11
12
Iterative Method
// Iterative Method (Queue)
function isSymmetric(root: TreeNode | null): boolean {
let helperQueue: (TreeNode | null)[] = [];
let tempNode1: TreeNode | null,
tempNode2: TreeNode | null;
if (root !== null) {
helperQueue.push(root.left);
helperQueue.push(root.right);
}
while (helperQueue.length > 0) {
tempNode1 = helperQueue.shift()!;
tempNode2 = helperQueue.shift()!;
if (tempNode1 === null && tempNode2 === null) continue;
if (tempNode1 === null || tempNode2 === null) return false;
if (tempNode1.val !== tempNode2.val) return false;
helperQueue.push(tempNode1.left);
helperQueue.push(tempNode2.right);
helperQueue.push(tempNode1.right);
helperQueue.push(tempNode2.left);
}
return true;
}
// Iterative Method (Stack)
function isSymmetric(root: TreeNode | null): boolean {
let helperStack: (TreeNode | null)[] = [];
let tempNode1: TreeNode | null,
tempNode2: TreeNode | null;
if (root !== null) {
helperStack.push(root.left);
helperStack.push(root.right);
}
while (helperStack.length > 0) {
tempNode1 = helperStack.pop()!;
tempNode2 = helperStack.pop()!;
if (tempNode1 === null && tempNode2 === null) continue;
if (tempNode1 === null || tempNode2 === null) return false;
if (tempNode1.val !== tempNode2.val) return false;
helperStack.push(tempNode1.left);
helperStack.push(tempNode2.right);
helperStack.push(tempNode1.right);
helperStack.push(tempNode2.left);
}
return true;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
# Swift:
Recursive
func isSymmetric(_ root: TreeNode?) -> Bool {
return _isSymmetric(root?.left, right: root?.right)
}
func _isSymmetric(_ left: TreeNode?, right: TreeNode?) -> Bool {
// First eliminate null node cases
if left == nil && right == nil {
return true
} else if left == nil && right != nil {
return false
} else if left != nil && right == nil {
return false
} else if left!.val != right!.val {
return false
}
// When left and right are both non-null and values are equal, recurse
let inSide = _isSymmetric(left!.right, right: right!.left)
let outSide = _isSymmetric(left!.left, right: right!.right)
return inSide && outSide
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Iterative - Using Queue
func isSymmetric2(_ root: TreeNode?) -> Bool {
guard let root = root else {
return true
}
var queue = [TreeNode?]()
queue.append(root.left)
queue.append(root.right)
while !queue.isEmpty {
let left = queue.removeFirst()
let right = queue.removeFirst()
if left == nil && right == nil {
continue
}
if left == nil || right == nil || left?.val != right?.val {
return false
}
queue.append(left!.left)
queue.append(right!.right)
queue.append(left!.right)
queue.append(right!.left)
}
return true
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Iterative - Using Stack
func isSymmetric3(_ root: TreeNode?) -> Bool {
guard let root = root else {
return true
}
var stack = [TreeNode?]()
stack.append(root.left)
stack.append(root.right)
while !stack.isEmpty {
let left = stack.removeLast()
let right = stack.removeLast()
if left == nil && right == nil {
continue
}
if left == nil || right == nil || left?.val != right?.val {
return false
}
stack.append(left!.left)
stack.append(right!.right)
stack.append(left!.right)
stack.append(right!.left)
}
return true
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# Scala:
Recursive:
object Solution {
def isSymmetric(root: TreeNode): Boolean = {
if (root == null) return true // Directly return true if null
def compare(left: TreeNode, right: TreeNode): Boolean = {
if (left == null && right == null) true // Symmetric if both are null
else if (left == null && right != null) false // Non-symmetric if left is null and right isn’t
else if (left != null && right == null) false // Non-symmetric if left isn’t null and right is
else left.value == right.value && compare(left.left, right.right) && compare(left.right, right.left)
}
// Compare left and right subtrees
compare(root.left, root.right)
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Iterative - Using Stack
object Solution {
import scala.collection.mutable
def isSymmetric(root: TreeNode): Boolean = {
if (root == null) return true
val cache = mutable.Stack[(TreeNode, TreeNode)]((root.left, root.right))
while (cache.nonEmpty) {
cache.pop() match {
case (null, null) =>
case (_, null) => return false
case (null, _) => return false
case (left, right) =>
if (left.value != right.value) return false
cache.push((left.left, right.right))
cache.push((left.right, right.left))
}
}
true
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Iterative - Using Queue
object Solution {
import scala.collection.mutable
def isSymmetric(root: TreeNode): Boolean = {
if (root == null) return true
val cache = mutable.Queue[(TreeNode, TreeNode)]((root.left, root.right))
while (cache.nonEmpty) {
cache.dequeue() match {
case (null, null) =>
case (_, null) => return false
case (null, _) => return false
case (left, right) =>
if (left.value != right.value) return false
cache.enqueue((left.left, right.right))
cache.enqueue((left.right, right.left))
}
}
true
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# Rust:
Recursive:
impl Solution {
pub fn is_symmetric(root: Option<Rc<RefCell<TreeNode>>>) -> bool {
Self::recur(
&root.as_ref().unwrap().borrow().left,
&root.as_ref().unwrap().borrow().right,
)
}
pub fn recur(
left: &Option<Rc<RefCell<TreeNode>>>,
right: &Option<Rc<RefCell<TreeNode>>>,
) -> bool {
match (left, right) {
(None, None) => true,
(Some(n1), Some(n2)) => {
return n1.borrow().val == n2.borrow().val
&& Self::recur(&n1.borrow().left, &n2.borrow().right)
&& Self::recur(&n1.borrow().right, &n2.borrow().left)
}
_ => false,
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Iterative:
use std::cell::RefCell;
use std::collections::VecDeque;
use std::rc::Rc;
impl Solution {
pub fn is_symmetric(root: Option<Rc<RefCell<TreeNode>>>) -> bool {
let mut queue = VecDeque::new();
if let Some(node) = root {
queue.push_back(node.borrow().left.clone());
queue.push_back(node.borrow().right.clone());
}
while !queue.is_empty() {
let (n1, n2) = (queue.pop_front().unwrap(), queue.pop_front().unwrap());
match (n1.clone(), n2.clone()) {
(None, None) => continue,
(Some(n1), Some(n2)) => {
if n1.borrow().val != n2.borrow().val {
return false;
}
}
_ => return false,
};
queue.push_back(n1.as_ref().unwrap().borrow().left.clone());
queue.push_back(n2.as_ref().unwrap().borrow().right.clone());
queue.push_back(n1.unwrap().borrow().right.clone());
queue.push_back(n2.unwrap().borrow().left.clone());
}
true
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# C#
// Recursive
public bool IsSymmetric(TreeNode root)
{
if (root == null) return true;
return Compare(root.left, root.right);
}
public bool Compare(TreeNode left, TreeNode right)
{
if(left == null && right != null) return false;
else if(left != null && right == null ) return false;
else if(left == null && right == null) return true;
else if(left.val != right.val) return false;
var outside = Compare(left.left, right.right);
var inside = Compare(left.right, right.left);
return outside&&inside;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// Iterative
public bool IsSymmetric(TreeNode root)
{
if (root == null) return true;
var st = new Stack<TreeNode>();
st.Push(root.left);
st.Push(root.right);
while (st.Count != 0)
{
var left = st.Pop();
var right = st.Pop();
if (left == null && right == null)
continue;
if ((left == null || right == null || (left.val != right.val)))
return false;
st.Push(left.left);
st.Push(right.right);
st.Push(left.right);
st.Push(right.left);
}
return true;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
