Leverage the properties of Binary Search Trees!

530. Minimum Absolute Difference in BST

LeetCode problem link (opens new window)

Given a binary search tree with non-negative values, find the minimum absolute difference between values of any two nodes.

Example:

Note: There are at least two nodes in the BST.

Approach

The task is to find the minimum absolute difference between any two nodes in a binary search tree.

Remember, it is a binary search tree, which is ordered.

Whenever you need to find max, min, or differences in a binary search tree, think of it as an ordered array, which simplifies the problem.

Recursive Approach

An in-order traversal of a binary search tree results in an ordered array.

Finding the minimum difference between two numbers in an ordered array is straightforward.

The most intuitive idea is to convert the binary search tree into an ordered array and then iterate through the array to find the minimum difference.

The code is as follows:

class Solution {
private:
vector<int> vec;
void traversal(TreeNode* root) {
    if (root == NULL) return;
    traversal(root->left);
    vec.push_back(root->val); // Convert the BST into an ordered array
    traversal(root->right);
}
public:
    int getMinimumDifference(TreeNode* root) {
        vec.clear();
        traversal(root);
        if (vec.size() < 2) return 0;
        int result = INT_MAX;
        for (int i = 1; i < vec.size(); i++) { // Find the minimum difference in the ordered array
            result = min(result, vec[i] - vec[i-1]);
        }
        return result;
    }
};

In the above code, we convert the binary search tree into an ordered array. We can calculate the difference as we traverse the tree.

We need to use a pre node to remember the previous node for this purpose.

As shown in the diagram:

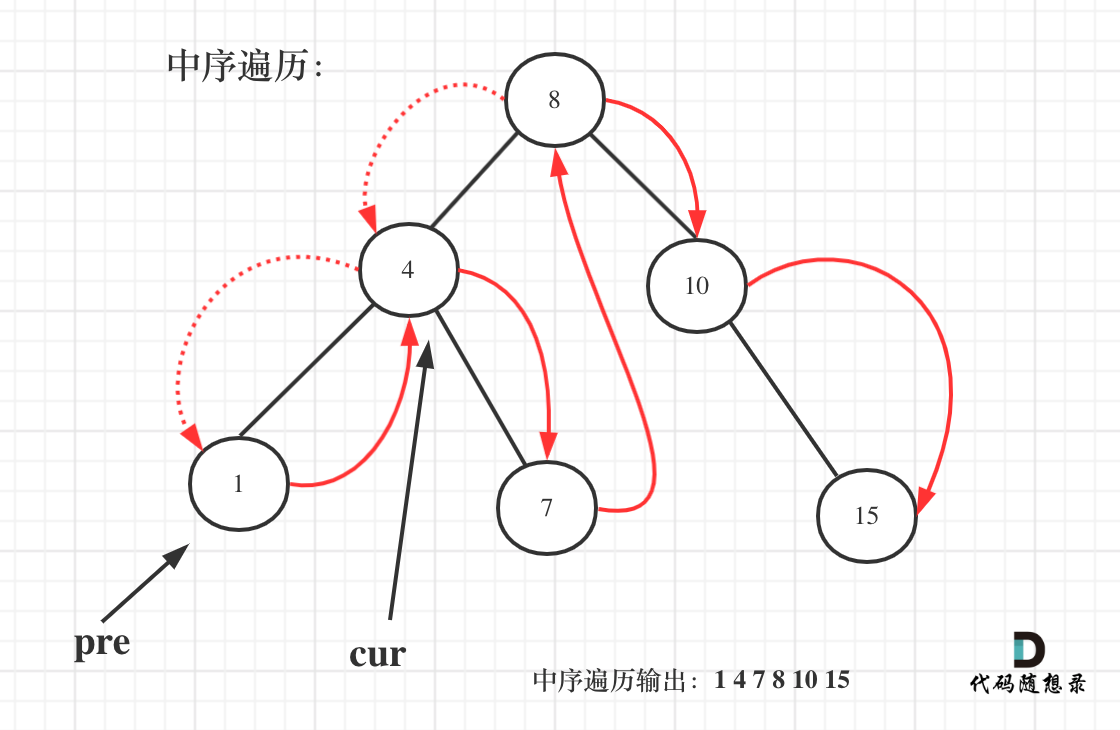
Some might not know how to maintain a pointer to the previous node in a recursive traversal. It's simple to implement and can be mastered once understood.

The code is as follows:

class Solution {
private:
int result = INT_MAX;
TreeNode* pre = NULL;
void traversal(TreeNode* cur) {
    if (cur == NULL) return;
    traversal(cur->left);   // Left
    if (pre != NULL){       // Middle
        result = min(result, cur->val - pre->val);
    }
    pre = cur; // Record previous
    traversal(cur->right);  // Right
}
public:
    int getMinimumDifference(TreeNode* root) {
        traversal(root);
        return result;
    }
};

Doesn't seem too complex, right?

Iterative Approach

After reading these two articles: Binary Tree: Anything Recursion Can Do, the Stack Can Do Too! (opens new window) and Binary Tree: Can’t We Unify the Methods of Preorder, Inorder, and Postorder Traversals? (opens new window), it's not hard to write the iterative in-order traversal for this problem.

Below is one way of writing the in-order traversal iteratively:

class Solution {
public:
    int getMinimumDifference(TreeNode* root) {
        stack<TreeNode*> st;
        TreeNode* cur = root;
        TreeNode* pre = NULL;
        int result = INT_MAX;
        while (cur != NULL || !st.empty()) {
            if (cur != NULL) { // Visit nodes by pointers, down to the bottom
                st.push(cur); // Add the visited nodes to the stack
                cur = cur->left;                // Left
            } else {
                cur = st.top();
                st.pop();
                if (pre != NULL) {              // Middle
                    result = min(result, cur->val - pre->val);
                }
                pre = cur;
                cur = cur->right;               // Right
            }
        }
        return result;
    }
};

Summary

When asked to find max/min value differences in a binary search tree, always think about the fact that a binary search tree is ordered and leverage that property.

Also, learn the small trick of maintaining two pointers during recursive traversal — once learned, it’s quite beneficial.

Next, I'll introduce a series of problems utilizing binary search tree properties.

Other Language Versions

Java

Recursive

class Solution {
    TreeNode pre; // Record the previously visited node
    int result = Integer.MAX_VALUE;

    public int getMinimumDifference(TreeNode root) {
        if (root == null)
            return 0;
        traversal(root);
        return result;
    }

    public void traversal(TreeNode root) {
        if (root == null)
            return;
        // Left
        traversal(root.left);
        // Middle
        if (pre != null) {
            result = Math.min(result, root.val - pre.val);
        }
        pre = root;
        // Right
        traversal(root.right);
    }
}

Unified Iterative Traversal

class Solution {
    public int getMinimumDifference(TreeNode root) {
        Stack<TreeNode> stack = new Stack<>();
        TreeNode pre = null;
        int result = Integer.MAX_VALUE;

        if (root != null)
            stack.add(root);

        while (!stack.isEmpty()) {
            TreeNode curr = stack.peek();
            if (curr != null) {
                stack.pop();
                if (curr.right != null)
                    stack.add(curr.right);
                stack.add(curr);
                stack.add(null);
                if (curr.left != null)
                    stack.add(curr.left);
            } else {
                stack.pop();
                TreeNode temp = stack.pop();
                if (pre != null)
                    result = Math.min(result, temp.val - pre.val);
                pre = temp;
            }
        }
        return result;
    }
}

Iterative In-order Traversal

class Solution {
    TreeNode pre;
    Stack<TreeNode> stack;
    public int getMinimumDifference(TreeNode root) {
        if (root == null) return 0;
        stack = new Stack<>();
        TreeNode cur = root;
        int result = Integer.MAX_VALUE;
        while (cur != null || !stack.isEmpty()) {
            if (cur != null) {
                stack.push(cur);
                cur = cur.left;
            } else {
                cur = stack.pop();
                if (pre != null) {
                    result = Math.min(result, cur.val - pre.val);
                }
                pre = cur;
                cur = cur.right;
            }
        }
        return result;
    }
}

Python

Recursive Version 1 - Using in-order traversal to build a sorted list

class Solution:
    def __init__(self):
        self.vec = []

    def traversal(self, root):
        if root is None:
            return
        self.traversal(root.left)
        self.vec.append(root.val)  # Convert the BST into an ordered array
        self.traversal(root.right)

    def getMinimumDifference(self, root):
        self.vec = []
        self.traversal(root)
        if len(self.vec) < 2:
            return 0
        result = float('inf')
        for i in range(1, len(self.vec)):
            # Find min difference in ordered array
            result = min(result, self.vec[i] - self.vec[i - 1])
        return result

Recursive Version 2 - Using in-order traversal to find the minimum difference

class Solution:
    def __init__(self):
        self.result = float('inf')
        self.pre = None

    def traversal(self, cur):
        if cur is None:
            return
        self.traversal(cur.left)  # Left
        if self.pre is not None:  # Middle
            self.result = min(self.result, cur.val - self.pre.val)
        self.pre = cur  # Record previous node
        self.traversal(cur.right)  # Right

    def getMinimumDifference(self, root):
        self.traversal(root)
        return self.result

Iterative Approach

class Solution:
    def getMinimumDifference(self, root):
        stack = []
        cur = root
        pre = None
        result = float('inf')

        while cur is not None or len(stack) > 0:
            if cur is not None:
                stack.append(cur)  # Add visited nodes to stack
                cur = cur.left  # Left
            else:
                cur = stack.pop()
                if pre is not None:  # Middle
                    result = min(result, cur.val - pre.val)
                pre = cur
                cur = cur.right  # Right

        return result

Go

Building a sorted array from the binary tree:

// Calculate minimum value during in-order traversal
func getMinimumDifference(root *TreeNode) int {
    // Keep a pointer to the previous node
    var prev *TreeNode
    // Define a very large value
    min := math.MaxInt64
    var travel func(node *TreeNode)
    travel = func(node *TreeNode) {
        if node == nil {
            return 
        }
        travel(node.Left)
        if prev != nil && node.Val - prev.Val < min {
            min = node.Val - prev.Val
        }
        prev = node
        travel(node.Right)
    }
    travel(root)
    return min
}

JavaScript

Recursive - First converting to a sorted array

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var getMinimumDifference = function (root) {
    let arr = [];
    const buildArr = (root) => {
        if (root) {
            buildArr(root.left);
            arr.push(root.val);
            buildArr(root.right);
        }
    }
    buildArr(root);
    let diff = arr[arr.length - 1];
    for (let i = 1; i < arr.length; ++i) {
        if (diff > arr[i] - arr[i - 1])
            diff = arr[i] - arr[i - 1];
    }
    return diff;
};

Recursive - Finding the minimum during traversal

var getMinimumDifference = function(root) {
    let res = Infinity
    let preNode = null
    const inorder = (node) => {
        if(!node) return
        inorder(node.left)
        if(preNode) res = Math.min(res, node.val - preNode.val)
        preNode = node
        inorder(node.right)
    }
    inorder(root)
    return res
}

Iterative - In-order traversal

var getMinimumDifference = function(root) {
    let stack = []
    let cur = root
    let res = Infinity
    let pre = null
    while(cur || stack.length) {
        if(cur) {
            stack.push(cur)
            cur = cur.left
        } else {
            cur = stack.pop()
            if(pre) res = Math.min(res, cur.val - pre.val)
            pre = cur
            cur = cur.right
        }
    }
    return res
}

TypeScript

Using auxiliary array to solve

function getMinimumDifference(root: TreeNode | null): number {
    let helperArr: number[] = [];
    function recur(root: TreeNode | null): void {
        if (root === null) return;
        recur(root.left);
        helperArr.push(root.val);
        recur(root.right);
    }
    recur(root);
    let resMin: number = Infinity;
    for (let i = 0, length = helperArr.length; i < length - 1; i++) {
        resMin = Math.min(resMin, helperArr[i + 1] - helperArr[i]);
    }
    return resMin;
};

Solving in recursion

function getMinimumDifference(root: TreeNode | null): number {
    let preNode: TreeNode | null= null;
    let resMin: number = Infinity;
    function recur(root: TreeNode | null): void {
        if (root === null) return;
        recur(root.left);
        if (preNode !== null) {
            resMin = Math.min(resMin, root.val - preNode.val);
        }
        preNode = root;
        recur(root.right);
    }
    recur(root);
    return resMin;
};

Iterative In-order Traversal

function getMinimumDifference(root: TreeNode | null): number {
    const helperStack: TreeNode[] = [];
    let curNode: TreeNode | null = root;
    let resMin: number = Infinity;
    let preNode: TreeNode | null = null;
    while (curNode !== null || helperStack.length > 0) {
        if (curNode !== null) {
            helperStack.push(curNode);
            curNode = curNode.left;
        } else {
            curNode = helperStack.pop()!;
            if (preNode !== null) {
                resMin = Math.min(resMin, curNode.val - preNode.val);
            }
            preNode = curNode;
            curNode = curNode.right;
        }
    }
    return resMin;
};

Scala

Creating a sorted array from the binary tree:

object Solution {
  import scala.collection.mutable
  def getMinimumDifference(root: TreeNode): Int = {
    val arr = mutable.ArrayBuffer[Int]()
    def traversal(node: TreeNode): Unit = {
      if (node == null) return
      traversal(node.left)
      arr.append(node.value)
      traversal(node.right)
    }
    traversal(root)
    var result = Int.MaxValue
    for (i <- 1 until arr.size) {
      result = math.min(result, arr(i) - arr(i - 1))
    }
    result
  }
}

Recording previous node during recursion:

object Solution {
  def getMinimumDifference(root: TreeNode): Int = {
    var result = Int.MaxValue
    var pre: TreeNode = null

    def traversal(cur: TreeNode): Unit = {
      if (cur == null) return
      traversal(cur.left)
      if (pre != null) {
        result = math.min(result, cur.value - pre.value)
      }
      pre = cur
      traversal(cur.right)
    }

    traversal(root)
    result
  }
}

Iterative solution:

object Solution {
  import scala.collection.mutable
  def getMinimumDifference(root: TreeNode): Int = {
    var result = Int.MaxValue
    var pre: TreeNode = null
    var cur = root
    var stack = mutable.Stack[TreeNode]()
    while (cur != null || !stack.isEmpty) {
      if (cur != null) {
        stack.push(cur)
        cur = cur.left
      } else {
        cur = stack.pop()
        if (pre != null) {
          result = math.min(result, cur.value - pre.value)
        }
        pre = cur
        cur = cur.right
      }
    }
    result
  }
}

Rust

Building a sorted array from the binary tree:

use std::cell::RefCell;
use std::rc::Rc;
impl Solution {
    pub fn get_minimum_difference(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
        let mut vec = vec![];
        Self::traversal(root, &mut vec);
        let mut min = i32::MAX;
        for i in 1..vec.len() {
            min = min.min(vec[i] - vec[i - 1])
        }
        min
    }
    pub fn traversal(root: Option<Rc<RefCell<TreeNode>>>, v: &mut Vec<i32>) {
        if root.is_none() {
            return;
        }
        let node = root.as_ref().unwrap().borrow();
        Self::traversal(node.left.clone(), v);
        v.push(node.val);
        Self::traversal(node.right.clone(), v);
    }
}

Calculating minimum during recursion

impl Solution {
    pub fn get_minimum_difference(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
        let mut pre = None;
        let mut min = i32::MAX;
        Self::inorder(root, &mut pre, &mut min);
        min
    }
    pub fn inorder(root: Option<Rc<RefCell<TreeNode>>>, pre: &mut Option<i32>, min: &mut i32) {
        if root.is_none() {
            return;
        }
        let node = root.as_ref().unwrap().borrow();
        Self::inorder(node.left.clone(), pre, min);
        if let Some(pre) = pre {
            *min = (node.val - *pre).min(*min);
        }
        *pre = Some(node.val);
        Self::inorder(node.right.clone(), pre, min);
    }
}

Iterative

impl Solution {
    pub fn get_minimum_difference(mut root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
        if root.is_none() {
            return 0;
        }
        let mut stack = vec![];
        let mut pre = -1;
        let mut res = i32::MAX;
        while root.is_some() || !stack.is_empty() {
            while let Some(node) = root {
                root = node.borrow().left.clone();
                stack.push(node);
            }

            let node = stack.pop().unwrap();

            if pre >= 0 {
                res = res.min(node.borrow().val - pre);
            }

            pre = node.borrow().val;

            root = node.borrow().right.clone();
        }
        res
    }
}

C#

// Recursive

public class Solution
{
    public List<int> res = new List<int>();
    public int GetMinimumDifference(TreeNode root)
    {
        Traversal(root);
        return res.SelectMany((x, i) => res.Skip(i + 1).Select(y => Math.Abs(x - y))).Min();
    }
    public void Traversal(TreeNode root)
    {
        if (root == null) return;
        Traversal(root.left);
        res.Add(root.val);
        Traversal(root.right);
    }
}