If you do not have a deep understanding of recursion, this problem can be quite challenging. Simply removing a node is not enough; you need to trim!
# 669. Trim a Binary Search Tree
LeetCode Problem Link (opens new window)
Given a binary search tree and the boundaries L and R, trim the tree so that all elements lie in [L, R] (R >= L). You might need to alter the root of the tree, so return the new root of the trimmed binary search tree.


# Approach
Many might perceive this as an easy problem (as labeled on LeetCode).
However, it is not that straightforward!
# Recursive Method
A straightforward approach would be to recursively process and return NULL when encountering root->val < low || root->val > high.
It is easy to write code like:
class Solution {
public:
TreeNode* trimBST(TreeNode* root, int low, int high) {
if (root == nullptr || root->val < low || root->val > high) return nullptr;
root->left = trimBST(root->left, low, high);
root->right = trimBST(root->right, low, high);
return root;
}
};
2
3
4
5
6
7
8
9
However, the [1, 3] interval in a binary search tree is not determined solely by node 3 and its left child node 0; you must also consider node 0's right subtree.
Let's focus on the second example again:
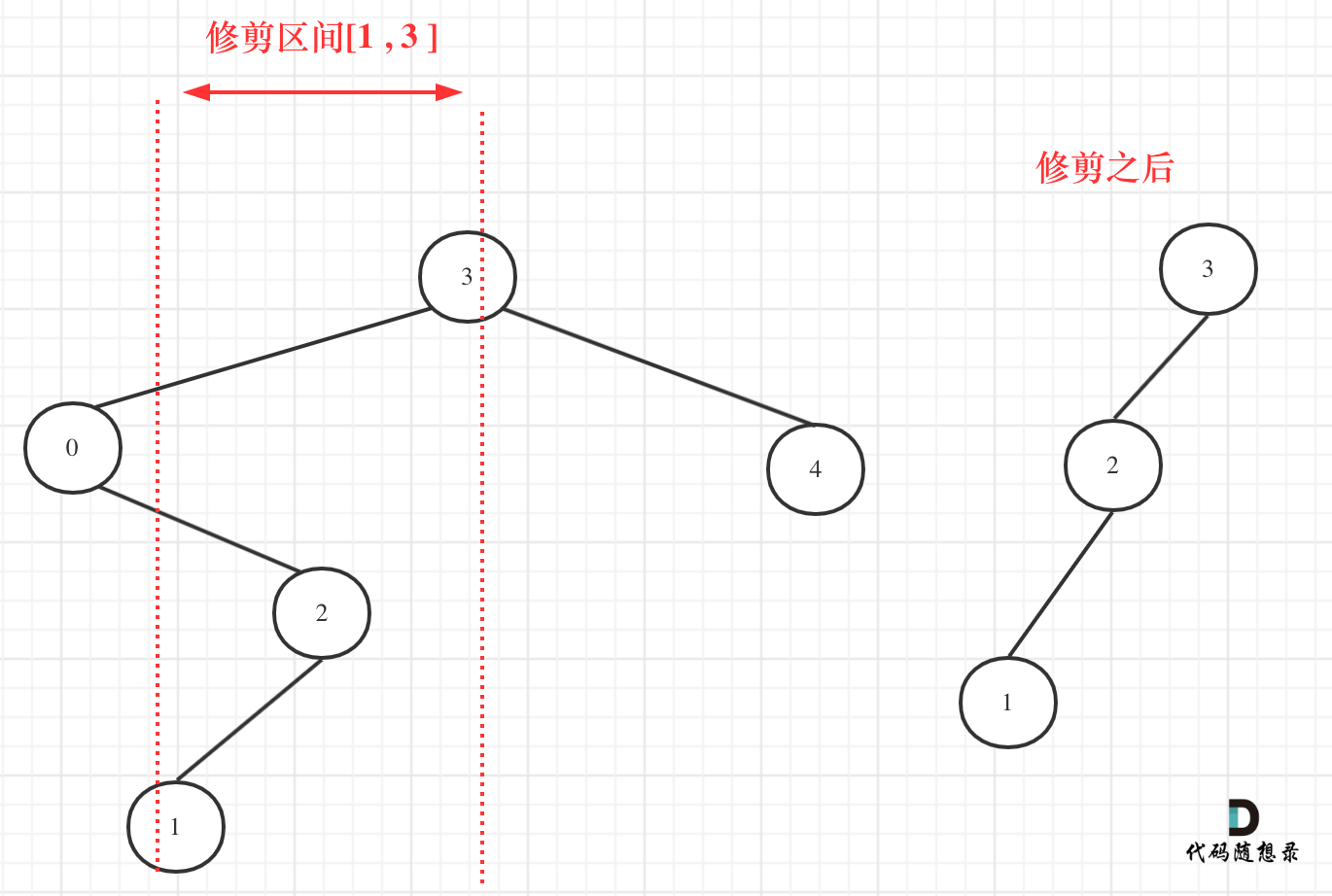
Thus, the above code is incorrect!
It is evident from the diagram that we need to reconstruct the binary tree, which indeed complicates the problem.
But it is not as complex as full reconstruction.
In the diagram, node 0 does not meet the boundary condition. Therefore, simply assigning node 0's right child, node 2, to node 3's left child will suffice (effectively removing node 0 from the tree), as shown:
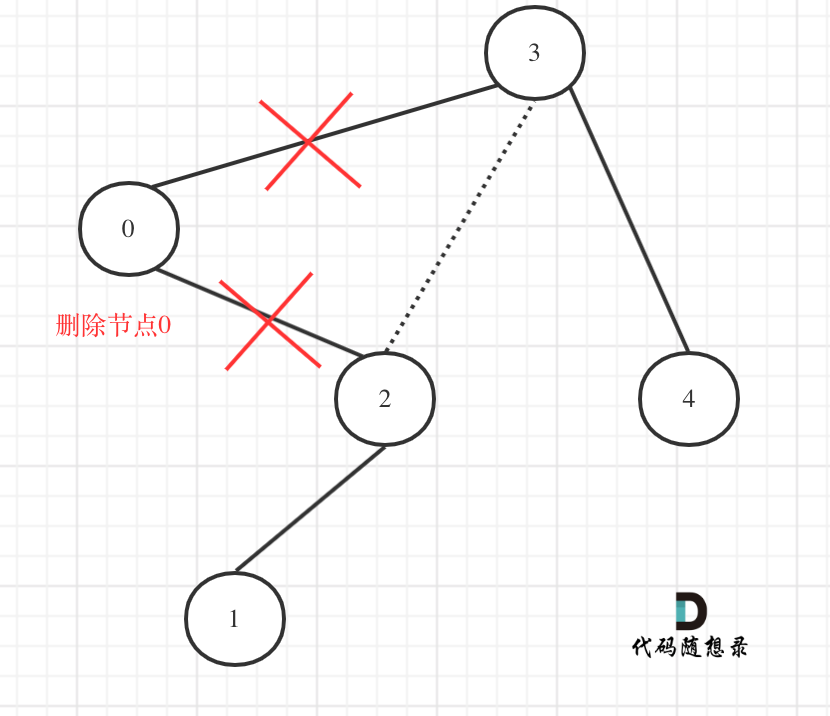
With the critical insight understood, let's proceed with the recursive three-step approach:
- Determine the function signature and return value
Why do we need a return value here?
Though you can trim (i.e., remove nodes from the tree) without a return value by traversing the entire tree and modifying it, using a return value simplifies the process by allowing us to remove nodes through it.
This approach was used in the explanations for 0701.Insert into a Binary Search Tree (opens new window) and 0450.Delete Node in a BST (opens new window).
TreeNode* trimBST(TreeNode* root, int low, int high)
- Identify the base case
Trimming is not performed at the base case, so if a node is null, simply return.
if (root == nullptr ) return nullptr;
- Define the logic for a single recursion step
If the root (current node) has a value less than low, recursively process the right subtree and return the head node of the right subtree that meets the condition.
if (root->val < low) {
TreeNode* right = trimBST(root->right, low, high); // Find nodes that meet [low, high]
return right;
}
2
3
4
If the root (current node) has a value greater than high, recursively process the left subtree and return the head node of the left subtree that meets the condition.
if (root->val > high) {
TreeNode* left = trimBST(root->left, low, high); // Find nodes that meet [low, high]
return left;
}
2
3
4
Next, assign the results of processing the left and right subtrees to root->left and root->right respectively:
root->left = trimBST(root->left, low, high); // Attach the left child meeting conditions
root->right = trimBST(root->right, low, high); // Attach the right child meeting conditions
return root;
2
3
You might wonder how exactly nodes are removed from the tree.
Re-examine the above code, considering the binary tree situation shown in the diagram:
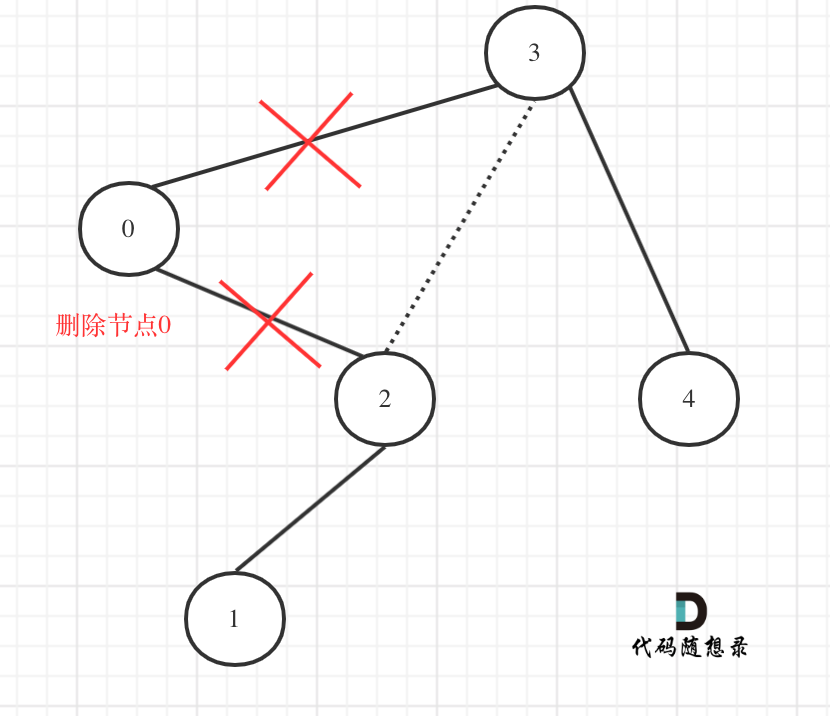
The following code effectively returns node 0's right child (node 2) to the previous layer:
if (root->val < low) {
TreeNode* right = trimBST(root->right, low, high); // Find nodes that meet [low, high]
return right;
}
2
3
4
Then, the following code assigns the returned node 2 (node 0's right child) to node 3's left child:
root->left = trimBST(root->left, low, high);
Thus, node 3's left child becomes node 2, removing node 0 from the tree.
Complete code:
class Solution {
public:
TreeNode* trimBST(TreeNode* root, int low, int high) {
if (root == nullptr ) return nullptr;
if (root->val < low) {
TreeNode* right = trimBST(root->right, low, high); // Find nodes that meet [low, high]
return right;
}
if (root->val > high) {
TreeNode* left = trimBST(root->left, low, high); // Find nodes that meet [low, high]
return left;
}
root->left = trimBST(root->left, low, high); // root->left attaches the left child meeting conditions
root->right = trimBST(root->right, low, high); // root->right attaches the right child meeting conditions
return root;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Refined code:
class Solution {
public:
TreeNode* trimBST(TreeNode* root, int low, int high) {
if (root == nullptr) return nullptr;
if (root->val < low) return trimBST(root->right, low, high);
if (root->val > high) return trimBST(root->left, low, high);
root->left = trimBST(root->left, low, high);
root->right = trimBST(root->right, low, high);
return root;
}
};
2
3
4
5
6
7
8
9
10
11
Just looking at the code, it might not be easy to understand how nodes are removed. You can simulate it to better grasp the concept!
# Iterative Method
Due to the ordered nature of the binary search tree, there is no need to use a stack to simulate the recursive process.
When trimming, it can be divided into three steps:
- Move the root to be within the
[L, R]range, noting it is left-closed and right-closed. - Trim the left subtree.
- Trim the right subtree.
Here is the code:
class Solution {
public:
TreeNode* trimBST(TreeNode* root, int L, int R) {
if (!root) return nullptr;
// Move root to be within the `[L, R]` range:
while (root != nullptr && (root->val < L || root->val > R)) {
if (root->val < L) root = root->right; // Move right if less than L
else root = root->left; // Move left if greater than R
}
TreeNode *cur = root;
// Root is within [L, R], handle left child elements less than L
while (cur != nullptr) {
while (cur->left && cur->left->val < L) {
cur->left = cur->left->right;
}
cur = cur->left;
}
cur = root;
// Root is within [L, R], handle right child elements greater than R
while (cur != nullptr) {
while (cur->right && cur->right->val > R) {
cur->right = cur->right->left;
}
cur = cur->right;
}
return root;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# Summary
Trimming a binary search tree is not overly difficult, but the recursive explanation required significant effort to detail the node removal method, and this concept can be quite intricate.
Ultimately, the code is quite concise.
If you do not have a deep understanding of recursion, this problem is challenging!
I have provided both recursive and iterative methods in this explanation. Beginners can focus on mastering recursion and then try the iterative method for further study.
# Other Language Versions
# Java
Recursive
class Solution {
public TreeNode trimBST(TreeNode root, int low, int high) {
if (root == null) {
return null;
}
if (root.val < low) {
return trimBST(root.right, low, high);
}
if (root.val > high) {
return trimBST(root.left, low, high);
}
// root is within [low, high]
root.left = trimBST(root.left, low, high);
root.right = trimBST(root.right, low, high);
return root;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Iterative
class Solution {
// iteration
public TreeNode trimBST(TreeNode root, int low, int high) {
if(root == null)
return null;
while(root != null && (root.val < low || root.val > high)){
if(root.val < low)
root = root.right;
else
root = root.left;
}
TreeNode curr = root;
// deal with root's left sub-tree, and elements smaller than low.
while(curr != null){
while(curr.left != null && curr.left.val < low){
curr.left = curr.left.right;
}
curr = curr.left;
}
// go back to root;
curr = root;
// deal with root's right sub-tree, and elements greater than high.
while(curr != null){
while(curr.right != null && curr.right.val > high){
curr.right = curr.right.left;
}
curr = curr.right;
}
return root;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
# Python
Recursive (Version 1)
class Solution:
def trimBST(self, root: TreeNode, low: int, high: int) -> TreeNode:
if root is None:
return None
if root.val < low:
# Find the subtree that meets [low, high]
return self.trimBST(root.right, low, high)
if root.val > high:
# Find the subtree that meets [low, high]
return self.trimBST(root.left, low, high)
root.left = self.trimBST(root.left, low, high) # Connect left child meeting conditions
root.right = self.trimBST(root.right, low, high) # Connect right child meeting conditions
return root
2
3
4
5
6
7
8
9
10
11
12
13
Iterative
class Solution:
def trimBST(self, root: TreeNode, L: int, R: int) -> TreeNode:
if not root:
return None
# Move root to be within the [L, R] range
while root and (root.val < L or root.val > R):
if root.val < L:
root = root.right # Move right if less than L
else:
root = root.left # Move left if greater than R
cur = root
# Root is within [L, R], handle elements less than L in left subtree
while cur:
while cur.left and cur.left.val < L:
cur.left = cur.left.right
cur = cur.left
cur = root
# Root is within [L, R], handle elements greater than R in right subtree
while cur:
while cur.right and cur.right.val > R:
cur.right = cur.right.left
cur = cur.right
return root
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# Go
// Recursive
func trimBST(root *TreeNode, low int, high int) *TreeNode {
if root == nil {
return nil
}
if root.Val < low { // If the node's value is less than low, move to the right
right := trimBST(root.Right, low, high)
return right
}
if root.Val > high { // If the node's value is more than high, move to the left
left := trimBST(root.Left, low, high)
return left
}
root.Left = trimBST(root.Left, low, high)
root.Right = trimBST(root.Right, low, high)
return root
}
// Iterative
func trimBST(root *TreeNode, low int, high int) *TreeNode {
if root == nil {
return nil
}
// Move the root to be within [low, high]:
for root != nil && (root.Val < low || root.Val > high) {
if root.Val < low {
root = root.Right
} else {
root = root.Left
}
}
cur := root
// With root having valid range, adjust the left subtree for values < low
while cur != nil {
while cur.Left != nil && cur.Left.Val < low {
cur.Left = cur.Left.Right
}
cur = cur.Left
}
cur = root
// Adjust the right subtree for values > high
while cur != nil {
while cur.Right != nil && cur.Right.Val > high {
cur.Right = cur.Right.Left
}
cur = cur.Right
}
return root
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
# JavaScript
Iterative:
var trimBST = function(root, low, high) {
if(root === null) {
return null;
}
while(root !== null && (root.val < low || root.val > high)) {
if(root.val < low) {
root = root.right;
}else {
root = root.left;
}
}
let cur = root;
while(cur !== null) {
while(cur.left && cur.left.val < low) {
cur.left = cur.left.right;
}
cur = cur.left;
}
cur = root;
// Handle right subtree > high
while(cur !== null) {
while(cur.right && cur.right.val > high) {
cur.right = cur.right.left;
}
cur = cur.right;
}
return root;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
Recursive:
var trimBST = function (root,low,high) {
if(root === null) {
return null;
}
if(root.val < low) {
let right = trimBST(root.right, low, high);
return right;
}
if(root.val > high) {
let left = trimBST(root.left, low, high);
return left;
}
root.left = trimBST(root.left, low, high);
root.right = trimBST(root.right, low, high);
return root;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# TypeScript
Recursive
function trimBST(root: TreeNode | null, low: number, high: number): TreeNode | null {
if (root === null) return null;
if (root.val < low) {
return trimBST(root.right, low, high);
}
if (root.val > high) {
return trimBST(root.left, low, high);
}
root.left = trimBST(root.left, low, high);
root.right = trimBST(root.right, low, high);
return root;
};
2
3
4
5
6
7
8
9
10
11
12
Iterative
function trimBST(root: TreeNode | null, low: number, high: number): TreeNode | null {
while (root !== null && (root.val < low || root.val > high)) {
if (root.val < low) {
root = root.right;
} else if (root.val > high) {
root = root.left;
}
}
let curNode: TreeNode | null = root;
while (curNode !== null) {
while (curNode.left !== null && curNode.left.val < low) {
curNode.left = curNode.left.right;
}
curNode = curNode.left;
}
curNode = root;
while (curNode !== null) {
while (curNode.right !== null && curNode.right.val > high) {
curNode.right = curNode.right.left;
}
curNode = curNode.right;
}
return root;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# Scala
Recursive Method:
object Solution {
def trimBST(root: TreeNode, low: Int, high: Int): TreeNode = {
if (root == null) return null
if (root.value < low) return trimBST(root.right, low, high)
if (root.value > high) return trimBST(root.left, low, high)
root.left = trimBST(root.left, low, high)
root.right = trimBST(root.right, low, high)
root
}
}
2
3
4
5
6
7
8
9
10
# Rust
// Recursive Method
impl Solution {
pub fn trim_bst(
root: Option<Rc<RefCell<TreeNode>>>,
low: i32,
high: i32,
) -> Option<Rc<RefCell<TreeNode>>> {
root.as_ref()?;
let mut node = root.as_ref().unwrap().borrow_mut();
if node.val < low {
return Self::trim_bst(node.right.clone(), low, high);
}
if node.val > high {
return Self::trim_bst(node.left.clone(), low, high);
}
node.left = Self::trim_bst(node.left.clone(), low, high);
node.right = Self::trim_bst(node.right.clone(), low, high);
drop(node);
root
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# C#
// Recursive
public TreeNode TrimBST(TreeNode root, int low, int high)
{
if (root == null) return null;
if (root.val < low)
return TrimBST(root.right, low, high);
if (root.val > high)
return TrimBST(root.left, low, high);
root.left = TrimBST(root.left, low, high);
root.right = TrimBST(root.right, low, high);
return root;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
