# 108. Convert Sorted Array to Binary Search Tree
LeetCode Problem Link (opens new window)
Convert an array sorted in ascending order into a height-balanced binary search tree.
In this problem, a height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differs by more than 1.
Example:

# Thought Process
Before tackling this problem, consider understanding the following topics:
- 0106.Construct Binary Tree from Inorder and Postorder Traversal (opens new window)
- 654.Maximum Binary Tree (opens new window) discusses how to construct a binary tree based on an array.
- 701.Insert into a Binary Search Tree (opens new window)
- 450.Delete Node in a BST (opens new window)
Let's dive into the main topic:
The problem states that we need to convert a sorted array into a height-balanced binary search tree. Why emphasize balance?
Given a sorted array, without the balance requirement, we could construct a binary search tree in a linear structure.
For example, given the sorted array [-10, -3, 0, 5, 9], one could create a binary search tree like the one shown below.
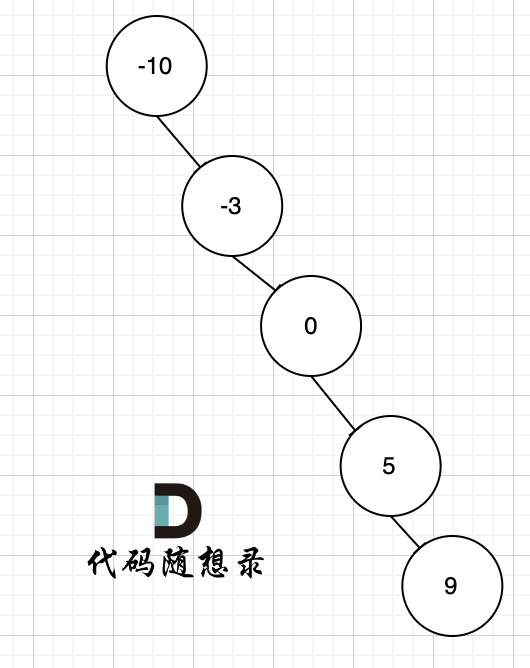
The above tree does conform to the properties of a binary search tree, but if created in this way, the problem would lose its significance, which is why balance is emphasized.
In fact, constructing a balanced tree from an array is quite natural, as it is commonly done by taking the middle value of the array to create nodes, and not doing so involves more effort. So trying to make an imbalanced binary tree is seeking trouble.
In 0106.Construct Binary Tree from Inorder and Postorder Traversal (opens new window) and 654.Maximum Binary Tree (opens new window), we've discussed how to construct a binary tree from an array.
The key idea is to identify a dividing point, making it the current node, and recursively handling the left and right subarrays.
Compared to 0106.Construct Binary Tree from Inorder and Postorder Traversal (opens new window) and 654.Maximum Binary Tree (opens new window), this problem is slightly easier because finding the dividing points in a sorted array to create a binary search tree is straightforward.
The dividing point is simply the middle element of the array.
What if the array's length is even and there are two middle nodes? Which one should be chosen?
Any choice is acceptable, but they result in different balanced binary search trees.
For instance, given input [-10, -3, 0, 5, 9], both of the following trees can be balanced binary search trees derived from this array:
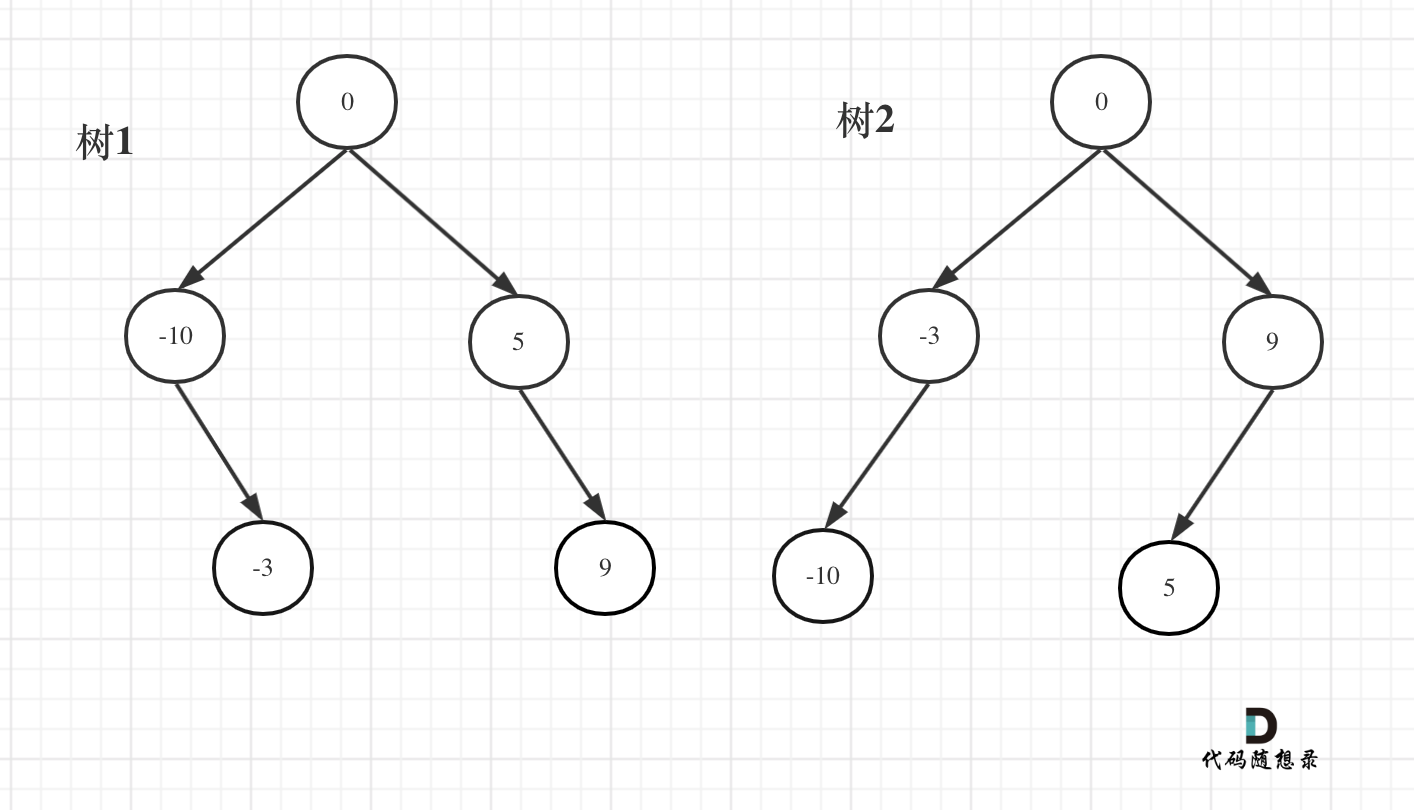
If the array length to be divided is even and there are two middle nodes, choosing the left one results in Tree 1, and choosing the right one leads to Tree 2.
This is why the problem statement mentions that the answer isn't unique. If you understand this point, you've grasped the essence of the problem.
# Recursion
Three Steps of Recursion:
- Define the return value and parameters of the recursive function
Adding or removing nodes in a binary tree is usually executed using the return value of a recursive function, making it quite convenient.
If you've had a detailed look at 701.Insert into a Binary Search Tree (opens new window) and 450.Delete Node in a BST (opens new window), you should find the pivotal role of return values in recursive functions quite clear.
In this problem, we use the return value of the recursive function to construct the node and its children.
Regarding parameters, we start with the passed array, and then have left and right indices. In 0106.Construct Binary Tree from Inorder and Postorder Traversal (opens new window), we mentioned that when constructing binary trees, it is usually better to use indices to manipulate the original array rather than redefining left and right subarrays.
So, the code structure is as follows:
// Closed interval [left, right]
TreeNode* traversal(vector<int>& nums, int left, int right)
2
Note here, I'm defining a closed interval from both left and right, and in the process of continually dividing it, I'll persist with maintaining a closed interval, which involves adhering to what we've discussed about invariants.
In 0106.Construct Binary Tree from Inorder and Postorder Traversal (opens new window), 035.Search Insert Position (opens new window), and 059.Spiral Matrix II (opens new window), we've thoroughly emphasized the importance of maintaining invariants.
- Define the termination condition of recursion
Here we are working with a closed interval [left, right], so when the interval is such that left > right, it denotes an empty node.
The code is as follows:
if (left > right) return nullptr;
- Define the logic of a single level of recursion
First, determine the middle index of the array, which is easily written as int mid = (left + right) / 2;. Writing it this way can indeed cause a problem, due to numeric overflow when both left and right are the maximum int size; this issue is especially prevalent in binary search (opens new window)!
Thus, it can be written as: int mid = left + ((right - left) / 2);
This problem's leetcode test data won’t exceed the maximum, so either way of writing is fine. But having such awareness is essential!
Once the middle is determined, construct a node using the element at this index: TreeNode* root = new TreeNode(nums[mid]);.
Then, dividing further, the root's left child captures the next level's left subarray's node, and the right child captures that of the right subarray.
Finally, return the root node. The complete code for a single-level recursion is as follows:
int mid = left + ((right - left) / 2);
TreeNode* root = new TreeNode(nums[mid]);
root->left = traversal(nums, left, mid - 1);
root->right = traversal(nums, mid + 1, right);
return root;
2
3
4
5
Here, int mid = left + ((right - left) / 2); implies selecting the left middle element when the array length is even.
- The complete recursive code is as follows:
class Solution {
private:
TreeNode* traversal(vector<int>& nums, int left, int right) {
if (left > right) return nullptr;
int mid = left + ((right - left) / 2);
TreeNode* root = new TreeNode(nums[mid]);
root->left = traversal(nums, left, mid - 1);
root->right = traversal(nums, mid + 1, right);
return root;
}
public:
TreeNode* sortedArrayToBST(vector<int>& nums) {
TreeNode* root = traversal(nums, 0, nums.size() - 1);
return root;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Note: When calling the traversal function, the values for left and right are from 0 to nums.size() - 1 because the interval is defined to be closed on both sides.
# Iterative Method
The iterative method can be mimicked using three queues: one for storing the nodes being traversed, one for left interval indices, and one for right interval indices.
Simply simulate the process of continual division, as shown in the C++ code below (with detailed comments):
class Solution {
public:
TreeNode* sortedArrayToBST(vector<int>& nums) {
if (nums.size() == 0) return nullptr;
TreeNode* root = new TreeNode(0); // Initial root node
queue<TreeNode*> nodeQue; // Queue to store traversed nodes
queue<int> leftQue; // Queue to store left interval indices
queue<int> rightQue; // Queue to store right interval indices
nodeQue.push(root); // Push the root node into the queue
leftQue.push(0); // Initial position for left interval index is 0
rightQue.push(nums.size() - 1); // Initial position for right interval index is nums.size() - 1
while (!nodeQue.empty()) {
TreeNode* curNode = nodeQue.front();
nodeQue.pop();
int left = leftQue.front(); leftQue.pop();
int right = rightQue.front(); rightQue.pop();
int mid = left + ((right - left) / 2);
curNode->val = nums[mid]; // Assign the element corresponding to mid to the current node
if (left <= mid - 1) { // Process the left interval
curNode->left = new TreeNode(0);
nodeQue.push(curNode->left);
leftQue.push(left);
rightQue.push(mid - 1);
}
if (right >= mid + 1) { // Process the right interval
curNode->right = new TreeNode(0);
nodeQue.push(curNode->right);
leftQue.push(mid + 1);
rightQue.push(right);
}
}
return root;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
# Summary
After 0106.Construct Binary Tree from Inorder and Postorder Traversal (opens new window) and 654.Maximum Binary Tree (opens new window), constructing a binary search tree using ordered arrays seems like a natural progression, leading to a balanced binary search tree with ease.
The thought process is essentially the same: continue dividing at the middle point, then recursively handle the left and right subarrays, making it a form of division and conquest.
At this point, one should be quite familiar with the use of recursive function return values to add or delete nodes in binary trees, which by now should be considered a routine operation.
During interval definition, we've once more underscored the vital importance of maintaining invariants.
Lastly, we again present the iterative method, which essentially simulates the process of picking middle elements and continuously dividing to form a binary tree.
# Other Language Versions
# Java
Recursion: Closed-open [left,right)
class Solution {
public TreeNode sortedArrayToBST(int[] nums) {
return sortedArrayToBST(nums, 0, nums.length);
}
public TreeNode sortedArrayToBST(int[] nums, int left, int right) {
if (left >= right) {
return null;
}
if (right - left == 1) {
return new TreeNode(nums[left]);
}
int mid = left + (right - left) / 2;
TreeNode root = new TreeNode(nums[mid]);
root.left = sortedArrayToBST(nums, left, mid);
root.right = sortedArrayToBST(nums, mid + 1, right);
return root;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Recursion: Closed interval [left, right]
class Solution {
public TreeNode sortedArrayToBST(int[] nums) {
TreeNode root = traversal(nums, 0, nums.length - 1);
return root;
}
// Closed interval [left, right]
private TreeNode traversal(int[] nums, int left, int right) {
if (left > right) return null;
int mid = left + ((right - left) >> 1);
TreeNode root = new TreeNode(nums[mid]);
root.left = traversal(nums, left, mid - 1);
root.right = traversal(nums, mid + 1, right);
return root;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Iterative: Closed interval [left, right]
class Solution {
public TreeNode sortedArrayToBST(int[] nums) {
if (nums.length == 0) return null;
// Initialize root node
TreeNode root = new TreeNode(-1);
Queue<TreeNode> nodeQueue = new LinkedList<>();
Queue<Integer> leftQueue = new LinkedList<>();
Queue<Integer> rightQueue = new LinkedList<>();
// Push root node into queue
nodeQueue.offer(root);
// 0 as the initial position for the left interval index
leftQueue.offer(0);
// nums.size() - 1 as the initial position for the right interval index
rightQueue.offer(nums.length - 1);
while (!nodeQueue.isEmpty()) {
TreeNode currNode = nodeQueue.poll();
int left = leftQueue.poll();
int right = rightQueue.poll();
int mid = left + ((right - left) >> 1);
// Assign the element corresponding to mid to the current node
currNode.val = nums[mid];
// Process the left interval
if (left <= mid - 1) {
currNode.left = new TreeNode(-1);
nodeQueue.offer(currNode.left);
leftQueue.offer(left);
rightQueue.offer(mid - 1);
}
// Process the right interval
if (right >= mid + 1) {
currNode.right = new TreeNode(-1);
nodeQueue.offer(currNode.right);
leftQueue.offer(mid + 1);
rightQueue.offer(right);
}
}
return root;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
# Python
Recursive method
class Solution:
def traversal(self, nums: List[int], left: int, right: int) -> TreeNode:
if left > right:
return None
mid = left + (right - left) // 2
root = TreeNode(nums[mid])
root.left = self.traversal(nums, left, mid - 1)
root.right = self.traversal(nums, mid + 1, right)
return root
def sortedArrayToBST(self, nums: List[int]) -> TreeNode:
root = self.traversal(nums, 0, len(nums) - 1)
return root
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Recursive method for brevity (self calling)
class Solution:
def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:
if not nums:
return
mid = len(nums) // 2
root = TreeNode(nums[mid])
root.left = self.sortedArrayToBST(nums[:mid])
root.right = self.sortedArrayToBST(nums[mid + 1 :])
return root
2
3
4
5
6
7
8
9
Iterative method
from collections import deque
class Solution:
def sortedArrayToBST(self, nums: List[int]) -> TreeNode:
if len(nums) == 0:
return None
root = TreeNode(0) # Initial root node
nodeQue = deque() # For traversed nodes
leftQue = deque() # For left interval indices
rightQue = deque() # For right interval indices
nodeQue.append(root) # Push root into the queue
leftQue.append(0) # Initial position for left index is 0
rightQue.append(len(nums) - 1) # Initial position for right index is len(nums) - 1
while nodeQue:
curNode = nodeQue.popleft()
left = leftQue.popleft()
right = rightQue.popleft()
mid = left + (right - left) // 2
curNode.val = nums[mid] # Assign the element at mid to the current node
if left <= mid - 1: # Process the left interval
curNode.left = TreeNode(0)
nodeQue.append(curNode.left)
leftQue.append(left)
rightQue.append(mid - 1)
if right >= mid + 1: # Process the right interval
curNode.right = TreeNode(0)
nodeQue.append(curNode.right)
leftQue.append(mid + 1)
rightQue.append(right)
return root
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
# Go
Recursive (implicit backtracking)
func sortedArrayToBST(nums []int) *TreeNode {
if len(nums) == 0 { // Termination condition: return when the array is empty
return nil
}
idx := len(nums)/2
root := &TreeNode{Val: nums[idx]}
root.Left = sortedArrayToBST(nums[:idx])
root.Right = sortedArrayToBST(nums[idx+1:])
return root
}
2
3
4
5
6
7
8
9
10
11
12
# JavaScript
Recursive
var sortedArrayToBST = function (nums) {
const buildTree = (Arr, left, right) => {
if (left > right)
return null;
let mid = Math.floor(left + (right - left) / 2);
let root = new TreeNode(Arr[mid]);
root.left = buildTree(Arr, left, mid - 1);
root.right = buildTree(Arr, mid + 1, right);
return root;
}
return buildTree(nums, 0, nums.length - 1);
};
2
3
4
5
6
7
8
9
10
11
12
13
14
Iterative
var sortedArrayToBST = function(nums) {
if(nums.length===0) {
return null;
}
let root = new TreeNode(0); // Initial root node
let nodeQue = [root]; // For traversing nodes, initialized
let leftQue = [0]; // For left interval indices, initialized
let rightQue = [nums.length-1]; // For right interval indices
while(nodeQue.length) {
let curNode = nodeQue.pop();
let left = leftQue.pop();
let right = rightQue.pop();
let mid = left + Math.floor((right-left)/2);
curNode.val = nums[mid]; // Assign the current node with the element indexed by mid
// Process the left interval
if(left <= mid-1) {
curNode.left = new TreeNode(0);
nodeQue.push(curNode.left);
leftQue.push(left);
rightQue.push(mid-1);
}
// Process the right interval
if(right >= mid+1) {
curNode.right = new TreeNode(0);
nodeQue.push(curNode.right);
leftQue.push(mid+1);
rightQue.push(right);
}
}
return root;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
# TypeScript
function sortedArrayToBST(nums: number[]): TreeNode | null {
function recur(nums: number[], left: number, right: number): TreeNode | null {
if (left > right) return null;
let mid: number = Math.floor((left + right) / 2);
const root: TreeNode = new TreeNode(nums[mid]);
root.left = recur(nums, left, mid - 1);
root.right = recur(nums, mid + 1, right);
return root;
}
return recur(nums, 0, nums.length - 1);
};
2
3
4
5
6
7
8
9
10
11
# C
Recursive
struct TreeNode* traversal(int* nums, int left, int right) {
if (left > right)
return NULL;
int mid = left + ((right - left) / 2);
struct TreeNode* root = (struct TreeNode*)malloc(sizeof(struct TreeNode));
root->val = nums[mid];
root->left = traversal(nums, left, mid - 1);
root->right = traversal(nums, mid + 1, right);
return root;
}
struct TreeNode* sortedArrayToBST(int* nums, int numsSize) {
struct TreeNode* root = traversal(nums, 0, numsSize - 1);
return root;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# Scala
Recursive:
object Solution {
def sortedArrayToBST(nums: Array[Int]): TreeNode = {
def buildTree(left: Int, right: Int): TreeNode = {
if (left > right) return null // Return null when left exceeds right
// The node in the middle is the current node
var mid = left + (right - left) / 2
var curNode = new TreeNode(nums(mid))
curNode.left = buildTree(left, mid - 1)
curNode.right = buildTree(mid + 1, right)
curNode
}
buildTree(0, nums.size - 1)
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
# Rust
Recursive:
impl Solution {
pub fn sorted_array_to_bst(nums: Vec<i32>) -> Option<Rc<RefCell<TreeNode>>> {
if nums.is_empty() {
return None;
}
let index = nums.len() / 2;
let mut root = TreeNode::new(nums[index]);
root.left = Self::sorted_array_to_bst(nums[..index].to_vec());
root.right = Self::sorted_array_to_bst(nums[index + 1..].to_vec());
Some(Rc::new(RefCell::new(root)))
}
}
2
3
4
5
6
7
8
9
10
11
12
13
# C#
// Recursive
public TreeNode SortedArrayToBST(int[] nums)
{
return Traversal(nums, 0, nums.Length - 1);
}
public TreeNode Traversal(int[] nums, int left, int right)
{
if (left > right) return null;
int mid = left + (right - left) / 2;
TreeNode node = new TreeNode(nums[mid]);
node.left = Traversal(nums, left, mid - 1);
node.right = Traversal(nums, mid + 1, right);
return node;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
