538. Convert BST to Greater Tree

LeetCode Problem Link (opens new window)

Given the root of a Binary Search Tree (BST) where node values are distinct, convert it to a Greater Sum Tree such that the value of each node node.val is replaced with the sum of all values greater than or equal to node.val.

Note that a binary search tree satisfies the following constraints:

• The left subtree of a node contains only nodes with keys less than the node’s key.
• The right subtree of a node contains only nodes with keys greater than the node’s key.
• Both the left and right subtrees must also be binary search trees.

Example 1:

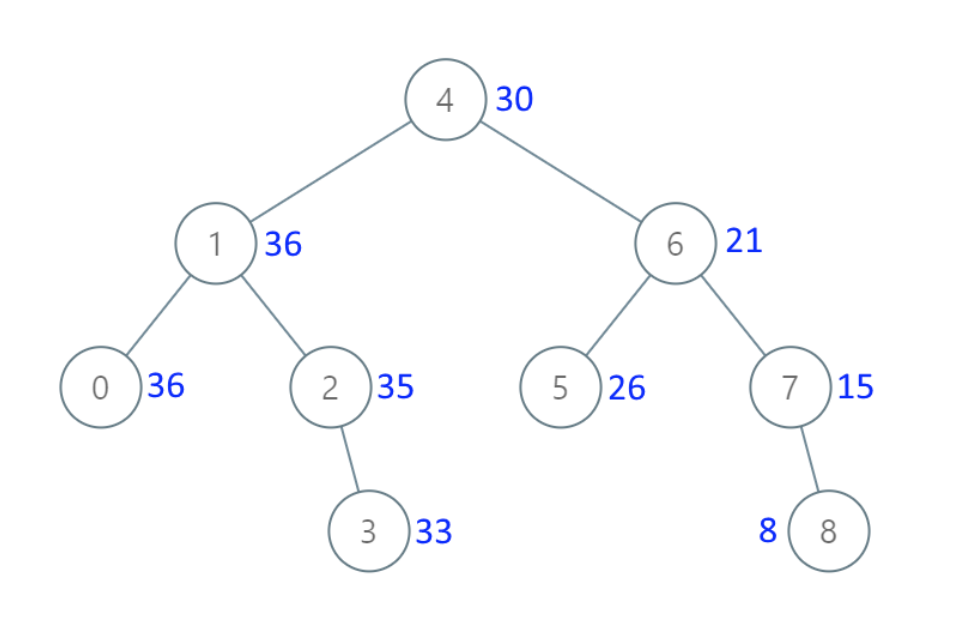
• Input: [4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
• Output: [30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

Example 2:

• Input: root = [0,null,1]
• Output: [1,null,1]

Example 3:

• Input: root = [1,0,2]
• Output: [3,3,2]

Example 4:

• Input: root = [3,2,4,1]
• Output: [7,9,4,10]

Constraints:

• The number of nodes in the tree is between 0 and 10^4.
• All node values are unique.
• The given tree is a binary search tree.

Strategy

When you first encounter the concept of a Greater Tree, you might wonder how to sum up the values. Should you traverse through other nodes and then accumulate the values for each node? That sounds quite cumbersome.

But then you realize it's a binary search tree, which is ordered.

So, how do you accumulate ordered elements?

This actually resembles transforming an ordered array like [2, 5, 13] to a cumulative array [20, 18, 13]. Doesn't that suddenly sound simple?

Why does it feel simpler when converting arrays?

Because you know how to traverse arrays, right? From back to front, accumulating one by one. This same logic applies to binary search trees; it's just a different representation.

Thus, this question boils down to how to traverse this binary tree. The solution is to perform a reverse in-order traversal (right-center-left) and accumulate the values in order.

Recursive Approach

The traversal sequence is shown in the image below:

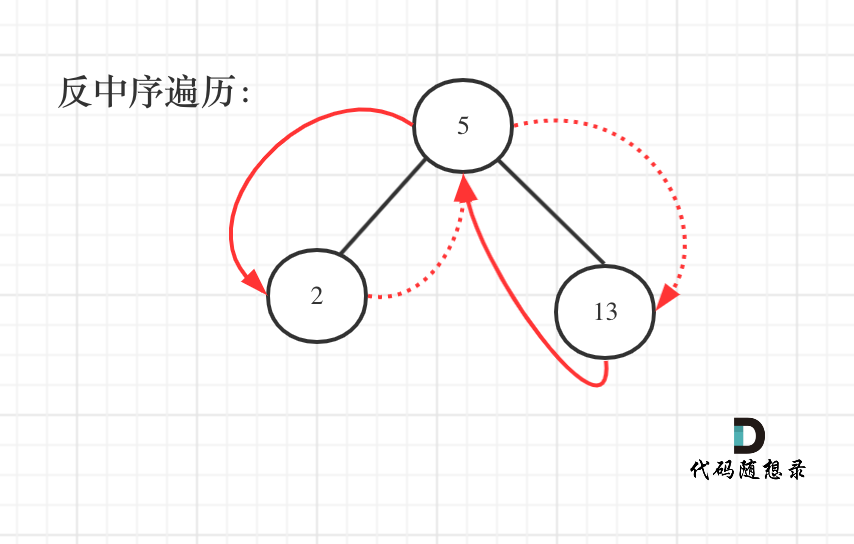
You will need a pre pointer in order to keep track of the previous node for accumulating the values during the traversal.

We previously introduced the use of the pre pointer in articles like 0530.Minimum Absolute Difference in BST (opens new window) and 0501.Find Mode in Binary Search Tree (opens new window). This is often useful for such operations.

• Define Parameters and Return Values:

Here, it's clear that the recursive function doesn’t need to return anything because the entire tree needs to be traversed.

We define a global pre variable to store the value of the previously traversed node.

int pre = 0; // Record the value of the previous node
void traversal(TreeNode* cur)

• Define the Termination Condition:

Terminate upon reaching a null node.

if (cur == NULL) return;

• Define the Logic for a Single Step in Recursion:

Note that we need to perform a reverse in-order traversal of the tree, and processing each node requires adding the value of the previous node to the current.

traversal(cur->right);  // Right
cur->val += pre;        // Center
pre = cur->val;
traversal(cur->left);   // Left

Here's the complete recursive solution in C++:

class Solution {
private:
    int pre = 0; // Record previous node value
    void traversal(TreeNode* cur) { // right-center-left traversal
        if (cur == NULL) return;
        traversal(cur->right);
        cur->val += pre;
        pre = cur->val;
        traversal(cur->left);
    }
public:
    TreeNode* convertBST(TreeNode* root) {
        pre = 0;
        traversal(root);
        return root;
    }
};

Iterative Approach

The iterative approach follows the template for in-order traversal, as elaborated in Binary Tree Iterative Traversal (opens new window) and Unified Iterative Traversal of Binary Tree (opens new window). Here’s one version:

class Solution {
private:
    int pre; // Record previous node value
    void traversal(TreeNode* root) {
        stack<TreeNode*> st;
        TreeNode* cur = root;
        while (cur != NULL || !st.empty()) {
            if (cur != NULL) {
                st.push(cur);
                cur = cur->right;   // Right
            } else {
                cur = st.top();     // Center
                st.pop();
                cur->val += pre;
                pre = cur->val;
                cur = cur->left;    // Left
            }
        }
    }
public:
    TreeNode* convertBST(TreeNode* root) {
        pre = 0;
        traversal(root);
        return root;
    }
};

Conclusion

After various operations such as insertion, deletion, and search in the previous binary tree problems, this problem should now seem relatively simple.

Finally, we are approaching the conclusion of binary trees, which will soon be followed by a comprehensive summary.

Other Language Versions

Java

Recursive

class Solution {
    int sum;
    public TreeNode convertBST(TreeNode root) {
        sum = 0;
        convertBST1(root);
        return root;
    }

    // Traverse in the order of right-center-left and accumulate values
    public void convertBST1(TreeNode root) {
        if (root == null) {
            return;
        }
        convertBST1(root.right);
        sum += root.val;
        root.val = sum;
        convertBST1(root.left);
    }
}

Iterative

class Solution {
    // DFS using a stack in iteration
    public TreeNode convertBST(TreeNode root) {
        int pre = 0;
        Stack<TreeNode> stack = new Stack<>();
        if(root == null) // edge case check
            return null;

        stack.add(root);

        while(!stack.isEmpty()){
            TreeNode curr = stack.peek();
            if(curr != null){ 
                stack.pop();
                if(curr.left != null)       // Left
                    stack.add(curr.left);
                stack.add(curr);            // Center
                stack.add(null);
                if(curr.right != null)      // Right
                    stack.add(curr.right);
            }else{
                stack.pop();
                TreeNode temp = stack.pop();
                temp.val += pre;
                pre = temp.val;
            }
        }
        return root;
    }
}

Python

Recursive (Version 1)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def convertBST(self, root: TreeNode) -> TreeNode:
        self.pre = 0  # Record previous node value
        self.traversal(root)
        return root

    def traversal(self, cur):
        if cur is None:
            return        
        self.traversal(cur.right)
        cur.val += self.pre
        self.pre = cur.val
        self.traversal(cur.left)

Recursive (Version 2)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def __init__(self):
        self.count = 0

    def convertBST(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        if root == None:
            return 
        # Convert by accumulating backwards
        self.convertBST(root.right)
        self.count += root.val
        root.val = self.count 
        self.convertBST(root.left)
        return root

Iterative (Version 1)

class Solution:
    def __init__(self):
        self.pre = 0  # Record previous node value
    
    def traversal(self, root):
        stack = []
        cur = root
        while cur or stack:
            if cur:
                stack.append(cur)
                cur = cur.right  # Right
            else:
                cur = stack.pop()  # Center
                cur.val += self.pre
                self.pre = cur.val
                cur = cur.left  # Left
    
    def convertBST(self, root):
        self.pre = 0
        self.traversal(root)
        return root

Iterative (Version 2)

class Solution:
    def convertBST(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        if not root: return root
        stack = []
        result = []
        cur = root
        pre = 0
        while cur or stack:
            if cur:
                stack.append(cur)
                cur = cur.right
            else: 
                cur = stack.pop()
                cur.val+= pre
                pre = cur.val
                cur =cur.left
        return root

Go

var pre int
func convertBST(root *TreeNode) *TreeNode {
    pre = 0
    traversal(root)
    return root
}

func traversal(cur *TreeNode) {
    if cur == nil {
        return
    }
    traversal(cur.Right)
    cur.Val += pre
    pre = cur.Val
    traversal(cur.Left)
}

JavaScript

Recursive

var convertBST = function(root) {
    let pre = 0;
    const ReverseInOrder = (cur) => {
        if(cur) {
            ReverseInOrder(cur.right);
            cur.val += pre;
            pre = cur.val;
            ReverseInOrder(cur.left);
        }
    }
    ReverseInOrder(root);
    return root;
};

Iterative

var convertBST = function (root) {
    let pre = 0;
    let cur = root;
    let stack = [];
    while (cur !== null || stack.length !== 0) {
        while (cur !== null) {
            stack.push(cur);
            cur = cur.right;
        }
        cur = stack.pop();
        cur.val += pre;
        pre = cur.val;
        cur = cur.left;
    }
    return root;
};

C

Recursive

int pre;
void traversal(struct TreeNode* node) {
    if(!node)
        return ;
    traversal(node->right);
    node->val = node->val + pre;
    pre = node->val;
    traversal(node->left);
}

struct TreeNode* convertBST(struct TreeNode* root){
    pre = 0;
    traversal(root);
    return root;
}

TypeScript

Recursive

function convertBST(root: TreeNode | null): TreeNode | null {
    let pre: number = 0;
    function recur(root: TreeNode | null): void {
        if (root === null) return;
        recur(root.right);
        root.val += pre;
        pre = root.val;
        recur(root.left);
    }
    recur(root);
    return root;
};

Iterative

function convertBST(root: TreeNode | null): TreeNode | null {
    const helperStack: TreeNode[] = [];
    let curNode: TreeNode | null = root;
    let pre: number = 0;
    while (curNode !== null || helperStack.length > 0) {
        while (curNode !== null) {
            helperStack.push(curNode);
            curNode = curNode.right;
        }
        curNode = helperStack.pop()!;
        curNode.val += pre;
        pre = curNode.val;
        curNode = curNode.left;
    }
    return root;
};

Scala

object Solution {
  def convertBST(root: TreeNode): TreeNode = {
    var sum = 0
    def convert(node: TreeNode): Unit = {
      if (node == null) return
      convert(node.right)
      sum += node.value
      node.value = sum
      convert(node.left)
    }
    convert(root)
    root
  }
}

Rust

Recursive:

impl Solution {
    pub fn convert_bst(root: Option<Rc<RefCell<TreeNode>>>) -> Option<Rc<RefCell<TreeNode>>> {
        let mut pre = 0;
        Self::traversal(&root, &mut pre);
        root
    }

    pub fn traversal(cur: &Option<Rc<RefCell<TreeNode>>>, pre: &mut i32) {
        if cur.is_none() {
            return;
        }
        let mut node = cur.as_ref().unwrap().borrow_mut();
        Self::traversal(&node.right, pre);
        *pre += node.val;
        node.val = *pre;
        Self::traversal(&node.left, pre);
    }
}

Iterative:

impl Solution {
    pub fn convert_bst(root: Option<Rc<RefCell<TreeNode>>>) -> Option<Rc<RefCell<TreeNode>>> {
        let mut cur = root.clone();
        let mut stack = vec![];
        let mut pre = 0;
        while !stack.is_empty() || cur.is_some() {
            while let Some(node) = cur {
                cur = node.borrow().right.clone();
                stack.push(node);
            }
            if let Some(node) = stack.pop() {
                pre += node.borrow().val;
                node.borrow_mut().val = pre;
                cur = node.borrow().left.clone();
            }
        }
        root
    }
}

C#

// Recursive
public class Solution
{
    int pre = 0;
    public TreeNode ConvertBST(TreeNode root)
    {
        if (root == null) return null;
        ConvertBST(root.right);
        root.val += pre;
        pre = root.val;
        ConvertBST(root.left);
        return root;
    }
}