# 226. Invert Binary Tree
LeetCode Problem Link (opens new window)
Invert a binary tree.

There's a heart-wrenching story about this problem. Reportedly, Max Howell, the author of Homebrew, was rejected by Google because he couldn't write the solution to invert a binary tree on a whiteboard. (This story's veracity is unconfirmed, take it as a lighthearted note.)
# Off-topic
This problem is a classic and relatively simple (at least intuitive to solve).
However, because it's so straightforward, some might rush through it without grasping the underlying concept, passing it without truly understanding. Even if you've solved this problem before, it's recommended to review thoroughly, as it might bring new insights!
# Approach
Previously, we've introduced various ways to traverse a binary tree. Now we need to invert it, which might seem confusing at first.
How should this inversion be done?
Looking at the whole tree, inverting indeed feels complex: you flip the tree along its central axis, as shown below:
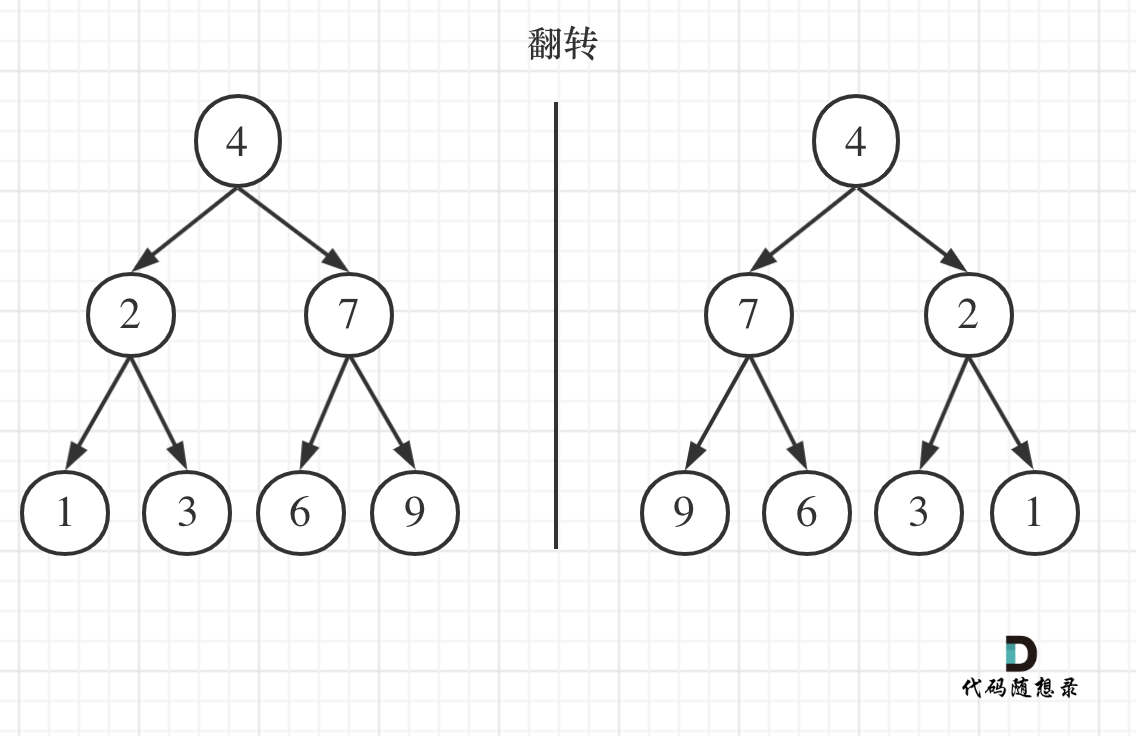
Upon closer observation, to invert it, you merely need to swap each node's left and right children.
The key lies in the order of traversal. Which traversal type should be used: preorder, inorder, or postorder? (Some who've solved this problem might not even know which traversal they used.)
During traversal, simply swapping each node's left and right children achieves the full inversion effect.
Note: Simply swap each node's left and right children to achieve an overall inversion effect.
This problem can be solved using preorder and postorder traversals, but not inorder, as inorder might result in some nodes getting their children swapped twice! A quick drawing can help illustrate this.
So, can level-order traversal be used? Absolutely! Any traversal method that swaps each node's left and right children works!
# Recursive Approach
We've previously detailed recursive preorder, inorder, and postorder traversals in Binary Tree Recursive Traversal (opens new window).
We'll use preorder traversal to illustrate the inversion process through an animation:

Let's break down the recursive approach into three steps:
- Determine the parameters and return value of the recursive function.
The main parameter is the node's pointer with no additional parameters required initially. Start with essential parameters, adding more if needed during logic development.
As for the return value, none is explicitly needed. However, since the problem requires returning the root node, we use the predefined function as is, with the return type TreeNode*.
TreeNode* invertTree(TreeNode* root)
- Set the termination condition.
Return when the current node is NULL.
if (root == NULL) return root;
- Define the logic for a single recursion layer.
Using preorder traversal, first swap the left and right children, then invert the left subtree, followed by the right subtree.
swap(root->left, root->right);
invertTree(root->left);
invertTree(root->right);
2
3
Based on the three steps above, the basic C++ code is as follows:
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if (root == NULL) return root;
swap(root->left, root->right); // Process current node
invertTree(root->left); // Left subtree
invertTree(root->right); // Right subtree
return root;
}
};
2
3
4
5
6
7
8
9
10
# Iterative Approach
# Depth-First Search
The method of iterative traversal using stacks, as demonstrated in Binary Tree Iterative Traversal (opens new window), allows us to easily code the iterative solution:
C++ Iterative Code (Preorder Traversal)
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if (root == NULL) return root;
stack<TreeNode*> st;
st.push(root);
while (!st.empty()) {
TreeNode* node = st.top(); // Process current node
st.pop();
swap(node->left, node->right);
if (node->right) st.push(node->right); // Right subtree
if (node->left) st.push(node->left); // Left subtree
}
return root;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
If the above code seems unclear, review Binary Tree Iterative Traversal (opens new window).
We've introduced a unified way to write preorder, inorder, and postorder iterations in Unified Iterative Traversal of Binary Tree (opens new window). Hence, modifying the provided code slightly suffices here too.
C++ Iterative Code (Preorder Traversal)
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
stack<TreeNode*> st;
if (root != NULL) st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();
if (node != NULL) {
st.pop();
if (node->right) st.push(node->right); // Right
if (node->left) st.push(node->left); // Left
st.push(node); // Process current node
st.push(NULL);
} else {
st.pop();
node = st.top();
st.pop();
swap(node->left, node->right); // Node processing logic
}
}
return root;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
If this code is not understandable, revisit Unified Iterative Traversal of Binary Tree (opens new window).
# Breadth-First Search
Also known as level-order traversal, it can invert the tree simply because it swaps each node's children once. The code is as follows:
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
queue<TreeNode*> que;
if (root != NULL) que.push(root);
while (!que.empty()) {
int size = que.size();
for (int i = 0; i < size; i++) {
TreeNode* node = que.front();
que.pop();
swap(node->left, node->right); // Node processing
if (node->left) que.push(node->left);
if (node->right) que.push(node->right);
}
}
return root;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
If the above code seems unclear, or you are unsure about the level-order traversal of binary trees, consider reading 0102.Binary Tree Level Order Traversal (opens new window).
# Extension
Note that I'm referring to recursive inorder traversal as being inefficient because it will swap some nodes' children twice.
A workaround to achieve the desired result with recursive inorder traversal is as follows:
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if (root == NULL) return root;
invertTree(root->left); // Left
swap(root->left, root->right); // Process current node
invertTree(root->left); // Note: Still need to traverse the left child since the parent node has been swapped
return root;
}
};
2
3
4
5
6
7
8
9
10
While the code is functional, it isn't truly an inorder transversal.
But using the iterative unified method for inorder traversal is feasible.
Here's the code:
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
stack<TreeNode*> st;
if (root != NULL) st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();
if (node != NULL) {
st.pop();
if (node->right) st.push(node->right); // Right
st.push(node); // Process current node
st.push(NULL);
if (node->left) st.push(node->left); // Left
} else {
st.pop();
node = st.top();
st.pop();
swap(node->left, node->right); // Node processing logic
}
}
return root;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
Why is this inorder traversal valid? Because it uses stacks rather than pointers to traverse, preventing the recursion method from swapping nodes twice. Visualize it, it's quite insightful.
# Conclusion
For binary tree problems, it's crucial to discern which traversal method—preorder, inorder, postorder, or level-order—applies before solving the problem.
The greatest pitfall in solving binary tree problems is being clueless about the method of traversal, even if the problem seems easy.
This is why binary tree problems are often described as "easy to understand, difficult to implement."
In the context of inverting a binary tree, I have demonstrated one recursive and three iterative approaches (two simulating depth-first search and one breadth-first search), utilizing previously discussed methods in a comprehensive manner.
There might be alternative solutions, but developing a methodological understanding is crucial for adaptability and application to similar problems.
# Other Language Versions
# Java:
//DFS recursive
class Solution {
/**
* Both preorder and postorder works
* Inorder won't work because when you first swap the left child's children and then the root's children,
* the right child becomes what used to be the left child, and swapping right child's children at this point
* would effectively be swapping the original left child's children.
*/
public TreeNode invertTree(TreeNode root) {
if (root == null) {
return null;
}
invertTree(root.left);
invertTree(root.right);
swapChildren(root);
return root;
}
private void swapChildren(TreeNode root) {
TreeNode tmp = root.left;
root.left = root.right;
root.right = tmp;
}
}
//BFS
class Solution {
public TreeNode invertTree(TreeNode root) {
if (root == null) {return null;}
ArrayDeque<TreeNode> deque = new ArrayDeque<>();
deque.offer(root);
while (!deque.isEmpty()) {
int size = deque.size();
while (size-- > 0) {
TreeNode node = deque.poll();
swap(node);
if (node.left != null) deque.offer(node.left);
if (node.right != null) deque.offer(node.right);
}
}
return root;
}
public void swap(TreeNode root) {
TreeNode temp = root.left;
root.left = root.right;
root.right = temp;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
# Python:
Recursive: Preorder Traversal:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def invertTree(self, root: TreeNode) -> TreeNode:
if not root:
return None
root.left, root.right = root.right, root.left
self.invertTree(root.left)
self.invertTree(root.right)
return root
2
3
4
5
6
7
8
9
10
11
12
13
14
Iterative: Preorder Traversal:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def invertTree(self, root: TreeNode) -> TreeNode:
if not root:
return None
stack = [root]
while stack:
node = stack.pop()
node.left, node.right = node.right, node.left
if node.right:
stack.append(node.right)
if node.left:
stack.append(node.left)
return root
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Recursive: Inorder Traversal:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def invertTree(self, root: TreeNode) -> TreeNode:
if not root:
return None
self.invertTree(root.left)
root.left, root.right = root.right, root.left
self.invertTree(root.left)
return root
2
3
4
5
6
7
8
9
10
11
12
13
14
Iterative: Simulating Inorder Traversal (result is correct; it looks like inorder traversal, but it's still preorder traversal with node processing logic moved to the middle):
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def invertTree(self, root: TreeNode) -> TreeNode:
if not root:
return None
stack = [root]
while stack:
node = stack.pop()
if node.right:
stack.append(node.right)
node.left, node.right = node.right, node.left # Placed in the middle, still preorder traversal
if node.right:
stack.append(node.right)
return root
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Recursive: Postorder Traversal:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def invertTree(self, root: TreeNode) -> TreeNode:
if not root:
return None
self.invertTree(root.left)
self.invertTree(root.right)
root.left, root.right = root.right, root.left
return root
2
3
4
5
6
7
8
9
10
11
12
13
14
Iterative: Simulating Postorder Traversal (result is correct; it looks like postorder traversal, but it's still preorder traversal with the node processing logic moved to the end):
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def invertTree(self, root: TreeNode) -> TreeNode:
if not root:
return None
stack = [root]
while stack:
node = stack.pop()
if node.right:
stack.append(node.right)
if node.left:
stack.append(node.left)
node.left, node.right = node.right, node.left
return root
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Iterative: Breadth-First Search (Level Order Traversal):
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def invertTree(self, root: TreeNode) -> TreeNode:
if not root:
return None
queue = collections.deque([root])
while queue:
node = queue.popleft()
node.left, node.right = node.right, node.left
if node.left: queue.append(node.left)
if node.right: queue.append(node.right)
return root
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# Go:
Recursive version using preorder traversal
func invertTree(root *TreeNode) *TreeNode {
if root == nil {
return nil
}
root.Left, root.Right = root.Right, root.Left // Swap
invertTree(root.Left)
invertTree(root.Right)
return root
}
2
3
4
5
6
7
8
9
10
11
Recursive version using postorder traversal
func invertTree(root *TreeNode) *TreeNode {
if root == nil {
return root
}
invertTree(root.Left) // Traverse left node
invertTree(root.Right) // Traverse right node
root.Left, root.Right = root.Right, root.Left // Swap
return root
}
2
3
4
5
6
7
8
9
10
11
Iterative version using preorder traversal
func invertTree(root *TreeNode) *TreeNode {
stack := []*TreeNode{}
node := root
for node != nil || len(stack) > 0 {
for node != nil {
node.Left, node.Right = node.Right, node.Left // Swap
stack = append(stack, node)
node = node.Left
}
node = stack[len(stack)-1]
stack = stack[:len(stack)-1]
node = node.Right
}
return root
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Iterative version using postorder traversal
func invertTree(root *TreeNode) *TreeNode {
stack := []*TreeNode{}
node := root
var prev *TreeNode
for node != nil || len(stack) > 0 {
for node != nil {
stack = append(stack, node)
node = node.Left
}
node = stack[len(stack)-1]
stack = stack[:len(stack)-1]
if node.Right == nil || node.Right == prev {
node.Left, node.Right = node.Right, node.Left // Swap
prev = node
node = nil
} else {
stack = append(stack, node)
node = node.Right
}
}
return root
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Level order traversal
func invertTree(root *TreeNode) *TreeNode {
if root == nil {
return root
}
queue := list.New()
node := root
queue.PushBack(node)
for queue.Len() > 0 {
length := queue.Len()
for i := 0; i < length; i++ {
e := queue.Remove(queue.Front()).(*TreeNode)
e.Left, e.Right = e.Right, e.Left // Swap
if e.Left != nil {
queue.PushBack(e.Left)
}
if e.Right != nil {
queue.PushBack(e.Right)
}
}
}
return root
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# JavaScript:
Using recursive version of preorder traversal
var invertTree = function(root) {
// Termination condition
if (!root) {
return null;
}
// Swap left and right nodes
const rightNode = root.right;
root.right = invertTree(root.left);
root.left = invertTree(rightNode);
return root;
};
2
3
4
5
6
7
8
9
10
11
Using iterative version (unified template) of preorder traversal:
var invertTree = function(root) {
// First define a node swap function
const invertNode = function(root, left, right) {
let temp = left;
left = right;
right = temp;
root.left = left;
root.right = right;
}
// Using iterative method's preorder traversal
let stack = [];
if(root === null) {
return root;
}
stack.push(root);
while(stack.length) {
let node = stack.pop();
if(node !== null) {
// Preorder traverse order is: node-left-right; stack order is in reverse: right-left-node
node.right && stack.push(node.right);
node.left && stack.push(node.left);
stack.push(node);
stack.push(null);
} else {
node = stack.pop();
// Node processing logic
invertNode(node, node.left, node.right);
}
}
return root;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
Using level order traversal:
var invertTree = function(root) {
// First define a node swap function
const invertNode = function(root, left, right) {
let temp = left;
left = right;
right = temp;
root.left = left;
root.right = right;
}
// Using level-order traversal
let queue = [];
if(root === null) {
return root;
}
queue.push(root);
while(queue.length) {
let length = queue.length;
while(length--) {
let node = queue.shift();
// Node processing logic
invertNode(node, node.left, node.right);
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
}
return root;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# TypeScript:
Recursive Method:
// Recursive Method (Preorder Traversal)
function invertTree(root: TreeNode | null): TreeNode | null {
if (root === null) return root;
let tempNode: TreeNode | null = root.left;
root.left = root.right;
root.right = tempNode;
invertTree(root.left);
invertTree(root.right);
return root;
};
// Recursive Method (Postorder Traversal)
function invertTree(root: TreeNode | null): TreeNode | null {
if (root === null) return root;
invertTree(root.left);
invertTree(root.right);
let tempNode: TreeNode | null = root.left;
root.left = root.right;
root.right = tempNode;
return root;
};
// Recursive Method (Inorder Traversal)
function invertTree(root: TreeNode | null): TreeNode | null {
if (root === null) return root;
invertTree(root.left);
let tempNode: TreeNode | null = root.left;
root.left = root.right;
root.right = tempNode;
// Since left and right nodes have already been swapped, root.left is now the original root.right
invertTree(root.left);
return root;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
Iterative Method:
// Iterative Method (Stack Simulating Preorder Traversal)
function invertTree(root: TreeNode | null): TreeNode | null {
let helperStack: TreeNode[] = [];
let curNode: TreeNode,
tempNode: TreeNode | null;
if (root !== null) helperStack.push(root);
while (helperStack.length > 0) {
curNode = helperStack.pop()!;
// It's best to perform stack operations before node weaving for clarity
if (curNode.right) helperStack.push(curNode.right);
if (curNode.left) helperStack.push(curNode.left);
tempNode = curNode.left;
curNode.left = curNode.right;
curNode.right = tempNode;
}
return root;
};
// Iterative Method (Stack Simulating Inorder Traversal - Unified Style)
function invertTree(root: TreeNode | null): TreeNode | null {
let helperStack: (TreeNode | null)[] = [];
let curNode: TreeNode | null,
tempNode: TreeNode | null;
if (root !== null) helperStack.push(root);
while (helperStack.length > 0) {
curNode = helperStack.pop();
if (curNode !== null) {
if (curNode.right !== null) helperStack.push(curNode.right);
helperStack.push(curNode);
helperStack.push(null);
if (curNode.left !== null) helperStack.push(curNode.left);
} else {
curNode = helperStack.pop()!;
tempNode = curNode.left;
curNode.left = curNode.right;
curNode.right = tempNode;
}
}
return root;
};
// Iterative Method (Stack Simulating Postorder Traversal - Unified Style)
function invertTree(root: TreeNode | null): TreeNode | null {
let helperStack: (TreeNode | null)[] = [];
let curNode: TreeNode | null,
tempNode: TreeNode | null;
if (root !== null) helperStack.push(root);
while (helperStack.length > 0) {
curNode = helperStack.pop();
if (curNode !== null) {
helperStack.push(curNode);
helperStack.push(null);
if (curNode.right !== null) helperStack.push(curNode.right);
if (curNode.left !== null) helperStack.push(curNode.left);
} else {
curNode = helperStack.pop()!;
tempNode = curNode.left;
curNode.left = curNode.right;
curNode.right = tempNode;
}
}
return root;
};
// Iterative Method (Queue Simulating Level Order Traversal)
function invertTree(root: TreeNode | null): TreeNode | null {
const helperQueue: TreeNode[] = [];
let curNode: TreeNode,
tempNode: TreeNode | null;
if (root !== null) helperQueue.push(root);
while (helperQueue.length > 0) {
for (let i = 0, length = helperQueue.length; i < length; i++) {
curNode = helperQueue.shift()!;
tempNode = curNode.left;
curNode.left = curNode.right;
curNode.right = tempNode;
if (curNode.left !== null) helperQueue.push(curNode.left);
if (curNode.right !== null) helperQueue.push(curNode.right);
}
}
return root;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
# C:
Recursive Method
struct TreeNode* invertTree(struct TreeNode* root){
if(!root)
return NULL;
// Swap node's left and right children (current)
struct TreeNode* temp = root->right;
root->right = root->left;
root->left = temp;
// Left
invertTree(root->left);
// Right
invertTree(root->right);
return root;
}
2
3
4
5
6
7
8
9
10
11
12
13
Iterative Method: Depth-First Search
struct TreeNode* invertTree(struct TreeNode* root){
if(!root)
return NULL;
// Stack to store the nodes
struct TreeNode** stack = (struct TreeNode**)malloc(sizeof(struct TreeNode*) * 100);
int stackTop = 0;
// Push the root into the stack
stack[stackTop++] = root;
// Continue if the stack still has elements
while(stackTop) {
// Remove the top element from the stack
struct TreeNode* temp = stack[--stackTop];
// Swap node's left and right children
struct TreeNode* tempNode = temp->right;
temp->right = temp->left;
temp->left = tempNode;
// If the current node has left and right children, push them into the stack
if(temp->right)
stack[stackTop++] = temp->right;
if(temp->left)
stack[stackTop++] = temp->left;
}
return root;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# Swift:
Preorder Traversal - Recursive
func invertTree(_ root: TreeNode?) -> TreeNode? {
guard let root = root else {
return root
}
let tmp = root.left
root.left = root.right
root.right = tmp
let _ = invertTree(root.left)
let _ = invertTree(root.right)
return root
}
// Level Order Traversal - Iterative
func invertTree1(_ root: TreeNode?) -> TreeNode? {
guard let root = root else {
return nil
}
var queue = [TreeNode]()
queue.append(root)
while !queue.isEmpty {
let node = queue.removeFirst()
let tmp = node.left
node.left = node.right
node.right = tmp
if let left = node.left {
queue.append(left)
}
if let right = node.right {
queue.append(right)
}
}
return root
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
Depth-First Search - Recursive
func invertTree(_ root: TreeNode?) -> TreeNode? {
guard let node = root else { return root }
swap(&node.left, &node.right)
_ = invertTree(node.left)
_ = invertTree(node.right)
return root
}
2
3
4
5
6
7
Depth-First Search - Iterative
func invertTree(_ root: TreeNode?) -> TreeNode? {
guard let node = root else { return root }
var stack = [node]
while !stack.isEmpty {
guard let node = stack.popLast() else { break }
swap(&node.left, &node.right)
if let node = node.left { stack.append(node) }
if let node = node.right { stack.append(node) }
}
return root
}
2
3
4
5
6
7
8
9
10
11
Breadth-First Search - Iterative
func invertTree(_ root: TreeNode?) -> TreeNode? {
guard let node = root else { return root }
var queue = [node]
while !queue.isEmpty {
let count = queue.count
for _ in 0 ..< count {
let node = queue.removeFirst()
swap(&node.left, &node.right)
if let node = node.left { queue.append(node) }
if let node = node.right { queue.append(node) }
}
}
return root
}
2
3
4
5
6
7
8
9
10
11
12
13
14
Depth-First Search (Preorder Traversal):
object Solution {
def invertTree(root: TreeNode): TreeNode = {
if (root == null) return root
// Recursive
def process(node: TreeNode): Unit = {
if (node == null) return
// Invert node
val curNode = node.left
node.left = node.right
node.right = curNode
process(node.left)
process(node.right)
}
process(root)
root
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Breadth-First Search (Level Order Traversal):
object Solution {
import scala.collection.mutable
def invertTree(root: TreeNode): TreeNode = {
if (root == null) return root
val queue = mutable.Queue[TreeNode]()
queue.enqueue(root)
while (!queue.isEmpty) {
val len = queue.size
for (i <- 0 until len) {
var curNode = queue.dequeue()
if (curNode.left != null) queue.enqueue(curNode.left)
if (curNode.right != null) queue.enqueue(curNode.right)
// Invert
var tmpNode = curNode.left
curNode.left = curNode.right
curNode.right = tmpNode
}
}
root
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# Rust:
impl Solution {
//* Recursive */
pub fn invert_tree(root: Option<Rc<RefCell<TreeNode>>>) -> Option<Rc<RefCell<TreeNode>>> {
if let Some(node) = root.as_ref() {
let (left, right) = (node.borrow().left.clone(), node.borrow().right.clone());
node.borrow_mut().left = Self::invert_tree(right);
node.borrow_mut().right = Self::invert_tree(left);
}
root
}
//* Iterative */
pub fn invert_tree(root: Option<Rc<RefCell<TreeNode>>>) -> Option<Rc<RefCell<TreeNode>>> {
let mut stack = vec![root.clone()];
while !stack.is_empty() {
if let Some(node) = stack.pop().unwrap() {
let (left, right) = (node.borrow().left.clone(), node.borrow().right.clone());
stack.push(right.clone());
stack.push(left.clone());
node.borrow_mut().left = right;
node.borrow_mut().right = left;
}
}
root
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# C#:
//Recursive
public class Solution {
public TreeNode InvertTree(TreeNode root) {
if (root == null) return root;
swap(root);
InvertTree(root.left);
InvertTree(root.right);
return root;
}
public void swap(TreeNode node) {
TreeNode temp = node.left;
node.left = node.right;
node.right = temp;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//Iterative
public class Solution {
public TreeNode InvertTree(TreeNode root) {
if(root == null) return root;
(root.left,root.right) = (root.right, root.left);
InvertTree(root.left);
InvertTree(root.right);
return root;
}
}
2
3
4
5
6
7
8
9
10
