# 404. Sum of Left Leaves
LeetCode Problem Link (opens new window)
Given a binary tree, calculate the sum of all left leaves in the tree.
Example:
# Approach
Firstly, note that it refers to left leaves, not the left-hand side of the binary tree, so do not immediately think of level-order traversal.
Since the problem does not clearly define a left leaf, let me provide a clear definition: Node A's left child is not null, and the left child has no children (meaning it is a leaf node), then Node A's left child is a left leaf node.
Consider the binary tree in the diagram below. What is the sum of its left leaves?
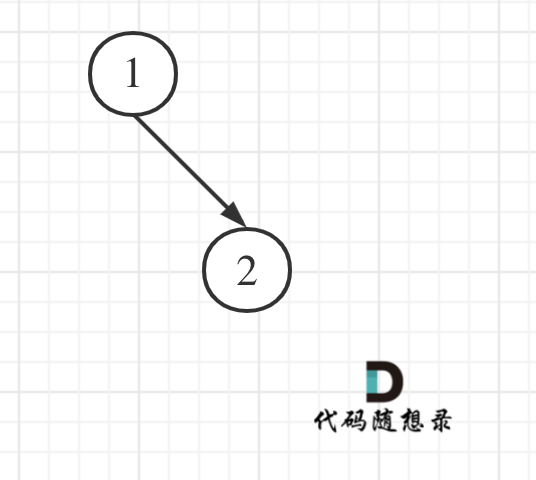It is actually 0 because this tree does not have any left leaves!
Now, what about the sum of left leaves in this tree?
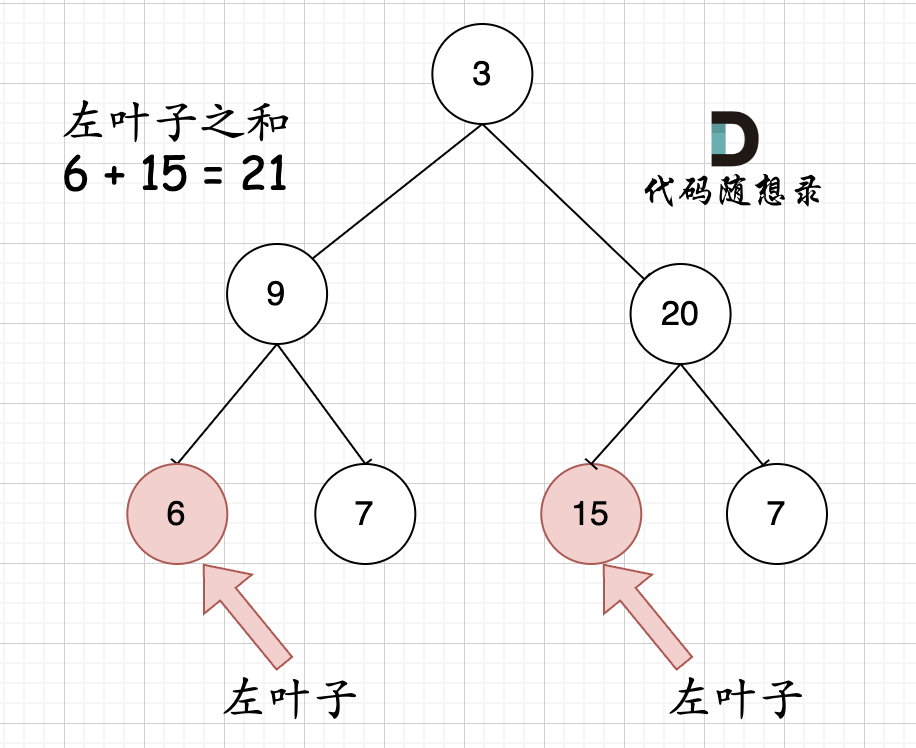
With these two illustrations, you should have a clear understanding of the definition of a left leaf.
The current node cannot determine if it is a left leaf; it has to be determined by the parent node.
If a node's left child is not null, and both of the left child's children are null, a left leaf has been found, processed by the following code:
if (node->left != NULL && node->left->left == NULL && node->left->right == NULL) {
// Logic for handling left leaf node
}
2
3
# Recursive Method
The recursive traversal order is post-order (left-right-root) because the sum of the values of left leaves is accumulated through the return value of the recursive function.
Recursive three-step process:
- Define the parameters and return value of the recursive function
To determine the sum of the left leaf nodes of a tree, the root of the tree must be provided, and the return value is the sum, so it is of type int.
Using the function provided in the problem is sufficient.
- Define the termination condition
If a null node is reached, the sum of left leaves is obviously 0
if (root == NULL) return 0;
Note that only when the current node is a parent can it be checked if its child is a left leaf. So if the current node traversed is a leaf node, then its left leaf must also be 0. Therefore, the termination condition is:
if (root == NULL) return 0;
if (root->left == NULL && root->right == NULL) return 0; // This line is optional: omitting it would not affect the result, but it would cause the recursion to go one layer deeper.
2
- Define the logic for a single level of recursion
When a left leaf is encountered, record its value, and then recursively calculate the sum of left leaves for the left and right subtrees, adding them to get the sum for the entire tree.
The code is as follows:
int leftValue = sumOfLeftLeaves(root->left); // Left
if (root->left && !root->left->left && !root->left->right) {
leftValue = root->left->val;
}
int rightValue = sumOfLeftLeaves(root->right); // Right
int sum = leftValue + rightValue; // Root
return sum;
2
3
4
5
6
7
8
The complete recursive code is as follows:
class Solution {
public:
int sumOfLeftLeaves(TreeNode* root) {
if (root == NULL) return 0;
if (root->left == NULL && root->right == NULL) return 0;
int leftValue = sumOfLeftLeaves(root->left); // Left
if (root->left && !root->left->left && !root->left->right) { // Left subtree is a left leaf situation
leftValue = root->left->val;
}
int rightValue = sumOfLeftLeaves(root->right); // Right
int sum = leftValue + rightValue; // Root
return sum;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
The refined code is as follows:
class Solution {
public:
int sumOfLeftLeaves(TreeNode* root) {
if (root == NULL) return 0;
int leftValue = 0;
if (root->left != NULL && root->left->left == NULL && root->left->right == NULL) {
leftValue = root->left->val;
}
return leftValue + sumOfLeftLeaves(root->left) + sumOfLeftLeaves(root->right);
}
};
2
3
4
5
6
7
8
9
10
11
The refined code doesn't really reveal the traversal method used. For beginners, learn from the first version.
# Iterative Method
This problem can be solved using pre-order, in-order, or post-order traversal as long as the left leaf nodes are identified. Referencing the article Binary Tree Iterative traversal (opens new window) and Unified Iterative Traversal of Binary Tree (opens new window), we can write an iterative pre-order traversal.
The judgment conditions are the same, and the code is as follows:
class Solution {
public:
int sumOfLeftLeaves(TreeNode* root) {
stack<TreeNode*> st;
if (root == NULL) return 0;
st.push(root);
int result = 0;
while (!st.empty()) {
TreeNode* node = st.top();
st.pop();
if (node->left != NULL && node->left->left == NULL && node->left->right == NULL) {
result += node->left->val;
}
if (node->right) st.push(node->right);
if (node->left) st.push(node->left);
}
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# Summary
This problem requires the sum of left leaves, which can be a bit tricky because it's not possible to determine whether the current node is a left leaf.
In this case, the identification of the left leaf must be determined by the parent node.
In our usual binary tree problem-solving, we are accustomed to determining a node's properties by its children. In this problem, we determine a node's property by its parent.
I hope this problem expands your binary tree problem-solving approach.
# Other Language Versions
# Java:
Recursive
class Solution {
public int sumOfLeftLeaves(TreeNode root) {
if (root == null) return 0;
int leftValue = sumOfLeftLeaves(root.left); // Left
int rightValue = sumOfLeftLeaves(root.right); // Right
int midValue = 0;
if (root.left != null && root.left.left == null && root.left.right == null) {
midValue = root.left.val;
}
int sum = midValue + leftValue + rightValue; // Root
return sum;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
Iterative
class Solution {
public int sumOfLeftLeaves(TreeNode root) {
if (root == null) return 0;
Stack<TreeNode> stack = new Stack<> ();
stack.add(root);
int result = 0;
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
if (node.left != null && node.left.left == null && node.left.right == null) {
result += node.left.val;
}
if (node.right != null) stack.add(node.right);
if (node.left != null) stack.add(node.left);
}
return result;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
// Level-order Traversal Iterative Method
class Solution {
public int sumOfLeftLeaves(TreeNode root) {
int sum = 0;
if (root == null) return 0;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
int size = queue.size();
while (size -- > 0) {
TreeNode node = queue.poll();
if (node.left != null) { // Left node is not null
queue.offer(node.left);
if (node.left.left == null && node.left.right == null){ // Left leaf node
sum += node.left.val;
}
}
if (node.right != null) queue.offer(node.right);
}
}
return sum;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# Python:
Recursive
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def sumOfLeftLeaves(self, root):
if root is None:
return 0
if root.left is None and root.right is None:
return 0
leftValue = self.sumOfLeftLeaves(root.left) # Left
if root.left and not root.left.left and not root.left.right: # Left subtree is a left leaf
leftValue = root.left.val
rightValue = self.sumOfLeftLeaves(root.right) # Right
sum_val = leftValue + rightValue # Root
return sum_val
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
Refined recursive version
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def sumOfLeftLeaves(self, root):
if root is None:
return 0
leftValue = 0
if root.left is not None and root.left.left is None and root.left.right is None:
leftValue = root.left.val
return leftValue + self.sumOfLeftLeaves(root.left) + self.sumOfLeftLeaves(root.right)
2
3
4
5
6
7
8
9
10
11
12
13
14
Iterative
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def sumOfLeftLeaves(self, root):
if root is None:
return 0
st = [root]
result = 0
while st:
node = st.pop()
if node.left and node.left.left is None and node.left.right is None:
result += node.left.val
if node.right:
st.append(node.right)
if node.left:
st.append(node.left)
return result
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# Go:
Recursive Method
func sumOfLeftLeaves(root *TreeNode) int {
if root == nil {
return 0
}
leftValue := sumOfLeftLeaves(root.Left) // Left
if root.Left != nil && root.Left.Left == nil && root.Left.Right == nil {
leftValue = root.Left.Val // Root
}
rightValue := sumOfLeftLeaves(root.Right) // Right
return leftValue + rightValue
}
2
3
4
5
6
7
8
9
10
11
12
13
14
Refined Recursive Version
func sumOfLeftLeaves(root *TreeNode) int {
if root == nil {
return 0
}
leftValue := 0
if root.Left != nil && root.Left.Left == nil && root.Left.Right == nil {
leftValue = root.Left.Val
}
return leftValue + sumOfLeftLeaves(root.Left) + sumOfLeftLeaves(root.Right)
}
2
3
4
5
6
7
8
9
10
Iterative Method (Pre-order Traversal)
func sumOfLeftLeaves(root *TreeNode) int {
st := make([]*TreeNode, 0)
if root == nil {
return 0
}
st = append(st, root)
result := 0
for len(st) != 0 {
node := st[len(st)-1]
st = st[:len(st)-1]
if node.Left != nil && node.Left.Left == nil && node.Left.Right == nil {
result += node.Left.Val
}
if node.Right != nil {
st = append(st, node.Right)
}
if node.Left != nil {
st = append(st, node.Left)
}
}
return result
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# JavaScript:
Recursive Method
var sumOfLeftLeaves = function(root) {
// Use post-order traversal recursively
// 1. Define recursion function parameters
const nodesSum = function(node) {
// 2. Define termination condition
if(node === null) {
return 0;
}
let leftValue = nodesSum(node.left);
let rightValue = nodesSum(node.right);
// 3. Single layer recursion logic
let midValue = 0;
if(node.left && node.left.left === null && node.left.right === null) {
midValue = node.left.val;
}
let sum = midValue + leftValue + rightValue;
return sum;
}
return nodesSum(root);
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Iterative Method
var sumOfLeftLeaves = function(root) {
// Use level-order traversal
if(root === null) {
return null;
}
let queue = [];
let sum = 0;
queue.push(root);
while(queue.length) {
let node = queue.shift();
if(node.left !== null && node.left.left === null && node.left.right === null) {
sum+=node.left.val;
}
node.left && queue.push(node.left);
node.right && queue.push(node.right);
}
return sum;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# TypeScript:
Recursive Method
function sumOfLeftLeaves(root: TreeNode | null): number {
if (root === null) return 0;
let midVal: number = 0;
if (
root.left !== null &&
root.left.left === null &&
root.left.right === null
) {
midVal = root.left.val;
}
let leftVal: number = sumOfLeftLeaves(root.left);
let rightVal: number = sumOfLeftLeaves(root.right);
return midVal + leftVal + rightVal;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
Iterative Method
function sumOfLeftLeaves(root: TreeNode | null): number {
let helperStack: TreeNode[] = [];
let tempNode: TreeNode;
let sum: number = 0;
if (root !== null) helperStack.push(root);
while (helperStack.length > 0) {
tempNode = helperStack.pop()!;
if (
tempNode.left !== null &&
tempNode.left.left === null &&
tempNode.left.right === null
) {
sum += tempNode.left.val;
}
if (tempNode.right !== null) helperStack.push(tempNode.right);
if (tempNode.left !== null) helperStack.push(tempNode.left);
}
return sum;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# Swift:
Recursive Method
func sumOfLeftLeaves(_ root: TreeNode?) -> Int {
guard let root = root else {
return 0
}
let leftValue = sumOfLeftLeaves(root.left)
let rightValue = sumOfLeftLeaves(root.right)
var midValue: Int = 0
if root.left != nil && root.left?.left == nil && root.left?.right == nil {
midValue = root.left!.val
}
let sum = midValue + leftValue + rightValue
return sum
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Iterative Method
func sumOfLeftLeaves(_ root: TreeNode?) -> Int {
guard let root = root else {
return 0
}
var stack = Array<TreeNode>()
stack.append(root)
var sum = 0
while !stack.isEmpty {
let lastNode = stack.removeLast()
if lastNode.left != nil && lastNode.left?.left == nil && lastNode.left?.right == nil {
sum += lastNode.left!.val
}
if let right = lastNode.right {
stack.append(right)
}
if let left = lastNode.left {
stack.append(left)
}
}
return sum
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# C:
Recursive method:
int sumOfLeftLeaves(struct TreeNode* root){
// Ending condition of recursion: if the current node is NULL, return 0
if(!root)
return 0;
// Recursively calculate the sum of the left node for the left and right subtrees
int leftValue = sumOfLeftLeaves(root->left);
int rightValue = sumOfLeftLeaves(root->right);
// If the left child of the current node exists and it is a leaf node, take its value
int midValue = 0;
if(root->left && (!root->left->left && !root->left->right))
midValue = root->left->val;
return leftValue + rightValue + midValue;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Iterative method:
int sumOfLeftLeaves(struct TreeNode* root){
struct TreeNode* stack[1000];
int stackTop = 0;
// If the root node passed in is not NULL, push it onto the stack
if(root)
stack[stackTop++] = root;
int sum = 0;
// Perform loop as long as stack is not empty
while(stackTop) {
// Pop the top element of the stack
struct TreeNode *topNode = stack[--stackTop];
// If the left child of the top element is a left leaf node, add its value to sum
if(topNode->left && (!topNode->left->left && !topNode->left->right))
sum += topNode->left->val;
// If the current top node has left and right children, push them onto the stack
if(topNode->right)
stack[stackTop++] = topNode->right;
if(topNode->left)
stack[stackTop++] = topNode->left;
}
return sum;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# Scala:
Recursive:
object Solution {
def sumOfLeftLeaves(root: TreeNode): Int = {
if(root == null) return 0
var midValue = 0
if(root.left != null && root.left.left == null && root.left.right == null){
midValue = root.left.value
}
// return keyword can be omitted
midValue + sumOfLeftLeaves(root.left) + sumOfLeftLeaves(root.right)
}
}
2
3
4
5
6
7
8
9
10
11
Iterative:
object Solution {
import scala.collection.mutable
def sumOfLeftLeaves(root: TreeNode): Int = {
val stack = mutable.Stack[TreeNode]()
if (root == null) return 0
stack.push(root)
var sum = 0
while (!stack.isEmpty) {
val curNode = stack.pop()
if (curNode.left != null && curNode.left.left == null && curNode.left.right == null) {
sum += curNode.left.value // Add if condition is satisfied
}
if (curNode.right != null) stack.push(curNode.right)
if (curNode.left != null) stack.push(curNode.left)
}
sum
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# Rust:
Recursive
use std::cell::RefCell;
use std::rc::Rc;
impl Solution {
pub fn sum_of_left_leaves(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
let mut res = 0;
if let Some(node) = root {
if let Some(left) = &node.borrow().left {
if left.borrow().right.is_none() && left.borrow().right.is_none() {
res += left.borrow().val;
}
}
res + Self::sum_of_left_leaves(node.borrow().left.clone())
+ Self::sum_of_left_leaves(node.borrow().right.clone())
} else {
0
}
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Iterative:
use std::cell::RefCell;
use std::rc::Rc;
impl Solution {
pub fn sum_of_left_leaves(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
let mut res = 0;
let mut stack = vec![root];
while !stack.is_empty() {
if let Some(node) = stack.pop().unwrap() {
if let Some(left) = &node.borrow().left {
if left.borrow().left.is_none() && left.borrow().right.is_none() {
res += left.borrow().val;
}
stack.push(Some(left.to_owned()));
}
if let Some(right) = &node.borrow().right {
stack.push(Some(right.to_owned()));
}
}
}
res
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# C#
// Recursive
public int SumOfLeftLeaves(TreeNode root)
{
if (root == null) return 0;
int leftValue = SumOfLeftLeaves(root.left);
if (root.left != null && root.left.left == null && root.left.right == null)
{
leftValue += root.left.val;
}
int rightValue = SumOfLeftLeaves(root.right);
return leftValue + rightValue;
}
2
3
4
5
6
7
8
9
10
11
12
13