# Unified Iteration Method for Binary Tree
# Concept
Previously, we implemented the preorder, inorder, and postorder traversals of binary trees using the recursive method in Binary Tree Recursive Traversal (opens new window).
In Binary Tree Iterative Traversal (opens new window), we used stacks to achieve iterative (non-recursive) traversals of binary trees for preorder, inorder, and postorder.
We later realized that the style of iterative methods for preorder, inorder, and postorder is not very unified. Preorder and postorder have some relation, but inorder looks entirely different, sometimes using the stack for traversal and other times using a pointer.
Those who have practiced might also find it difficult to write unified code using the iterative method for preorder, inorder, and postorder traversal, unlike the recursive method where after implementing one type of traversal, the others can be achieved by slightly altering the node sequence.
Actually, the iterative method can yield consistent style code for all three traversal methods!
Now, the main part is here. Let’s introduce the unified writing method.
Let's take inorder traversal as an example. In Binary Tree Iterative Traversal (opens new window), it was mentioned that using a stack can’t solve the situation where accessing a node (traversal node) and processing a node (adding the element to the result set) are inconsistent simultaneously.
So, we push the accessed nodes onto the stack and also push the nodes to be processed with a mark.
How can we mark them?
Method 1: Push the node to be processed onto the stack, followed by a null pointer as a mark. This method can be referred to as the
Null Pointer Marking Method.Method 2: Associate a
booleanvalue with each node, wherefalse(the default value) means that the node and its left and right children need arrangement in the stack, andtruemeans the node’s position is already arranged and can be processed. This can be called theBoolean Marking Method, sample code is shown below in theC++ and Python Boolean Marking Method. This method is easier to understand and easier to write in interviews.
# Iterative Inorder Traversal
Inorder traversal (Null Pointer Marking Method) code below: (Detailed comments)
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> result;
stack<TreeNode*> st;
if (root != NULL) st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();
if (node != NULL) {
st.pop();
if (node->right) st.push(node->right);
st.push(node);
st.push(nullptr);
if (node->left) st.push(node->left);
} else {
st.pop();
node = st.top();
st.pop();
result.push_back(node->val);
}
}
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
The code may seem abstract, so let's observe an animation (inorder traversal):
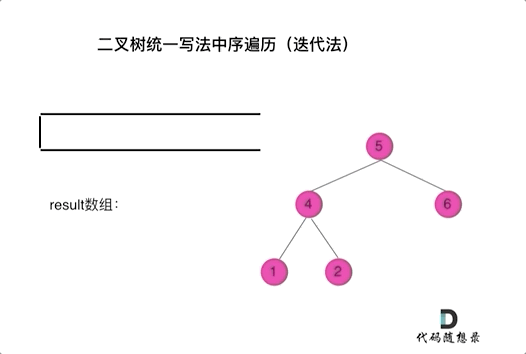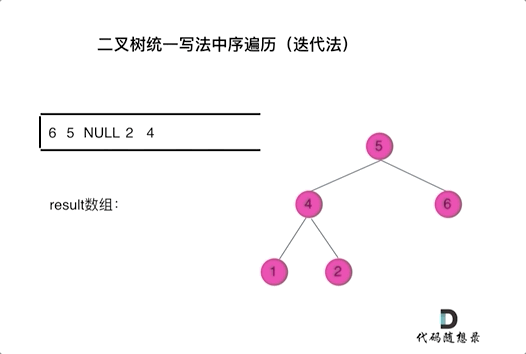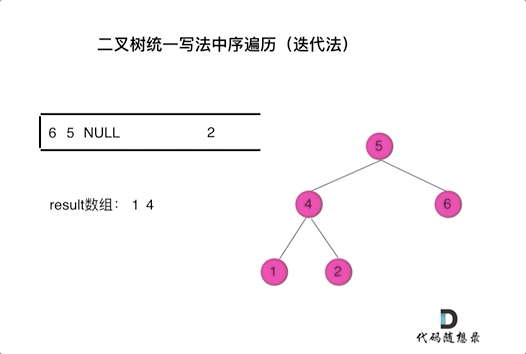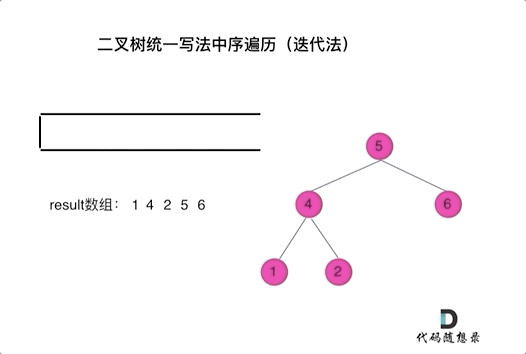
In the animation, the result array is the final result set.
We can see that we directly push accessed nodes onto the stack, but if it's a node to be processed, we push a null after it. Only when popping a null and the next node do we add it to the result set.
Inorder traversal (Boolean Marking Method):
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> result;
stack<pair<TreeNode*, bool>> st;
if (root != nullptr)
st.push(make_pair(root, false));
while (!st.empty()) {
auto node = st.top().first;
auto visited = st.top().second;
st.pop();
if (visited) {
result.push_back(node->val);
continue;
}
if (node->right)
st.push(make_pair(node->right, false));
st.push(make_pair(node, true));
if (node->left)
st.push(make_pair(node->left, false));
}
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Now, let's look at the preorder traversal code.
# Iterative Preorder Traversal
The iterative preorder traversal code is as follows: (Note that it's only a matter of changing the order of two lines of code compared to the inorder version)
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> result;
stack<TreeNode*> st;
if (root != NULL) st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();
if (node != NULL) {
st.pop();
if (node->right) st.push(node->right);
if (node->left) st.push(node->left);
st.push(node);
st.push(nullptr);
} else {
st.pop();
node = st.top();
st.pop();
result.push_back(node->val);
}
}
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# Iterative Postorder Traversal
The postorder traversal code is as follows: (Note that it's a matter of changing the order of two lines of code compared to the inorder version)
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> result;
stack<TreeNode*> st;
if (root != NULL) st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();
if (node != NULL) {
st.pop();
st.push(node);
st.push(nullptr);
if (node->right) st.push(node->right);
if (node->left) st.push(node->left);
} else {
st.pop();
node = st.top();
st.pop();
result.push_back(node->val);
}
}
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
Iterative postorder traversal (Boolean Marking Method):
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> result;
stack<pair<TreeNode*, bool>> st;
if (root != nullptr)
st.push(make_pair(root, false));
while (!st.empty()) {
auto node = st.top().first;
auto visited = st.top().second;
st.pop();
if (visited) {
result.push_back(node->val);
continue;
}
st.push(make_pair(node, true));
if (node->right)
st.push(make_pair(node->right, false));
if (node->left)
st.push(make_pair(node->left, false));
}
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# Summary
Now, we have written a unified style iterative method, and we no longer have to worry about getting the preorder right and struggling with inorder.
However, understanding the unified style iterative method is still challenging, and it can be difficult to write it directly in interviews.
So everyone should choose a style they find easier to understand for preorder, inorder, and postorder traversals, whether it's recursive or iterative.
# Other Language Versions
# Java:
Iterative preorder traversal code is as follows:
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> result = new LinkedList<>();
Stack<TreeNode> st = new Stack<>();
if (root != null) st.push(root);
while (!st.empty()) {
TreeNode node = st.peek();
if (node != null) {
st.pop();
if (node.right!=null) st.push(node.right);
if (node.left!=null) st.push(node.left);
st.push(node);
st.push(null);
} else {
st.pop();
node = st.peek();
st.pop();
result.add(node.val);
}
}
return result;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Iterative inorder traversal code is as follows:
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> result = new LinkedList<>();
Stack<TreeNode> st = new Stack<>();
if (root != null) st.push(root);
while (!st.empty()) {
TreeNode node = st.peek();
if (node != null) {
st.pop();
if (node.right!=null) st.push(node.right);
st.push(node);
st.push(null);
if (node.left!=null) st.push(node.left);
} else {
st.pop();
node = st.peek();
st.pop();
result.add(node.val);
}
}
return result;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Iterative postorder traversal code is as follows:
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> result = new LinkedList<>();
Stack<TreeNode> st = new Stack<>();
if (root != null) st.push(root);
while (!st.empty()) {
TreeNode node = st.peek();
if (node != null) {
st.pop();
st.push(node);
st.push(null);
if (node.right!=null) st.push(node.right);
if (node.left!=null) st.push(node.left);
} else {
st.pop();
node = st.peek();
st.pop();
result.add(node.val);
}
}
return result;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# Python:
Iterative preorder traversal (Null Pointer Marking Method):
class Solution:
def preorderTraversal(self, root: TreeNode) -> List[int]:
result = []
st= []
if root:
st.append(root)
while st:
node = st.pop()
if node != None:
if node.right:
st.append(node.right)
if node.left:
st.append(node.left)
st.append(node)
st.append(None)
else:
node = st.pop()
result.append(node.val)
return result
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Iterative inorder traversal (Null Pointer Marking Method):
class Solution:
def inorderTraversal(self, root: TreeNode) -> List[int]:
result = []
st = []
if root:
st.append(root)
while st:
node = st.pop()
if node != None:
if node.right:
st.append(node.right)
st.append(node)
st.append(None)
if node.left:
st.append(node.left)
else:
node = st.pop()
result.append(node.val)
return result
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
Iterative postorder traversal (Null Pointer Marking Method):
class Solution:
def postorderTraversal(self, root: TreeNode) -> List[int]:
result = []
st = []
if root:
st.append(root)
while st:
node = st.pop()
if node != None:
st.append(node)
st.append(None)
if node.right:
st.append(node.right)
if node.left:
st.append(node.left)
else:
node = st.pop()
result.append(node.val)
return result
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Inorder traversal, unified iteration (Boolean Marking Method):
class Solution:
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
values = []
stack = [(root, False)] if root else []
while stack:
node, visited = stack.pop()
if visited:
values.append(node.val)
continue
if node.right:
stack.append((node.right, False))
stack.append((node, True))
if node.left:
stack.append((node.left, False))
return values
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
Postorder traversal, unified iteration (Boolean Marking Method):
class Solution:
def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
values = []
stack = [(root, False)] if root else []
while stack:
node, visited = stack.pop()
if visited:
values.append(node.val)
continue
stack.append((node, True))
if node.right:
stack.append((node.right, False))
if node.left:
stack.append((node.left, False))
return values
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# Go:
Preorder traversal unified iteration method
func preorderTraversal(root *TreeNode) []int {
if root == nil {
return nil
}
var stack = list.New() // stack
res:=[]int{} // result set
stack.PushBack(root)
var node *TreeNode
for stack.Len()>0{
e := stack.Back()
stack.Remove(e)
if e.Value==nil{
e=stack.Back()
stack.Remove(e)
node=e.Value.(*TreeNode)
res=append(res,node.Val)
continue
}
node = e.Value.(*TreeNode)
if node.Right!=nil{
stack.PushBack(node.Right)
}
if node.Left!=nil{
stack.PushBack(node.Left)
}
stack.PushBack(node)
stack.PushBack(nil)
}
return res
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Inorder traversal unified iteration method
func inorderTraversal(root *TreeNode) []int {
if root==nil{
return nil
}
stack:=list.New()
res:=[]int{}
stack.PushBack(root)
var node *TreeNode
for stack.Len()>0{
e := stack.Back()
stack.Remove(e)
if e.Value==nil{
e=stack.Back()
stack.Remove(e)
node=e.Value.(*TreeNode)
res=append(res,node.Val)
continue
}
node = e.Value.(*TreeNode)
if node.Right!=nil{
stack.PushBack(node.Right)
}
stack.PushBack(node)
stack.PushBack(nil)
if node.Left!=nil{
stack.PushBack(node.Left)
}
}
return res
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Postorder traversal unified iteration method
func postorderTraversal(root *TreeNode) []int {
if root == nil {
return nil
}
var stack = list.New()
res := []int{}
stack.PushBack(root)
var node *TreeNode
for stack.Len() > 0 {
e := stack.Back()
stack.Remove(e)
if e.Value == nil {
e = stack.Back()
stack.Remove(e)
node = e.Value.(*TreeNode)
res = append(res, node.Val)
continue
}
node = e.Value.(*TreeNode)
stack.PushBack(node)
stack.PushBack(nil)
if node.Right != nil {
stack.PushBack(node.Right)
}
if node.Left != nil {
stack.PushBack(node.Left)
}
}
return res
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# JavaScript:
Preorder traversal unified iteration method
var preorderTraversal = function(root, res = []) {
const stack = [];
if (root) stack.push(root);
while(stack.length) {
const node = stack.pop();
if(!node) {
res.push(stack.pop().val);
continue;
}
if (node.right) stack.push(node.right);
if (node.left) stack.push(node.left);
stack.push(node);
stack.push(null);
};
return res;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Inorder traversal unified iteration method
var inorderTraversal = function(root, res = []) {
const stack = [];
if (root) stack.push(root);
while(stack.length) {
const node = stack.pop();
if(!node) {
res.push(stack.pop().val);
continue;
}
if (node.right) stack.push(node.right);
stack.push(node);
stack.push(null);
if (node.left) stack.push(node.left);
};
return res;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Postorder traversal unified iteration method
var postorderTraversal = function(root, res = []) {
const stack = [];
if (root) stack.push(root);
while(stack.length) {
const node = stack.pop();
if(!node) {
res.push(stack.pop().val);
continue;
}
stack.push(node);
stack.push(null);
if (node.right) stack.push(node.right);
if (node.left) stack.push(node.left);
};
return res;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# TypeScript:
// Preorder traversal (Iterative method)
function preorderTraversal(root: TreeNode | null): number[] {
let helperStack: (TreeNode | null)[] = [];
let res: number[] = [];
let curNode: TreeNode | null;
if (root === null) return res;
helperStack.push(root);
while (helperStack.length > 0) {
curNode = helperStack.pop()!;
if (curNode !== null) {
if (curNode.right !== null) helperStack.push(curNode.right);
if (curNode.left !== null) helperStack.push(curNode.left);
helperStack.push(curNode);
helperStack.push(null);
} else {
curNode = helperStack.pop()!;
res.push(curNode.val);
}
}
return res;
};
// Inorder traversal (Iterative method)
function inorderTraversal(root: TreeNode | null): number[] {
let helperStack: (TreeNode | null)[] = [];
let res: number[] = [];
let curNode: TreeNode | null;
if (root === null) return res;
helperStack.push(root);
while (helperStack.length > 0) {
curNode = helperStack.pop()!;
if (curNode !== null) {
if (curNode.right !== null) helperStack.push(curNode.right);
helperStack.push(curNode);
helperStack.push(null);
if (curNode.left !== null) helperStack.push(curNode.left);
} else {
curNode = helperStack.pop()!;
res.push(curNode.val);
}
}
return res;
};
// Postorder traversal (Iterative method)
function postorderTraversal(root: TreeNode | null): number[] {
let helperStack: (TreeNode | null)[] = [];
let res: number[] = [];
let curNode: TreeNode | null;
if (root === null) return res;
helperStack.push(root);
while (helperStack.length > 0) {
curNode = helperStack.pop()!;
if (curNode !== null) {
helperStack.push(curNode);
helperStack.push(null);
if (curNode.right !== null) helperStack.push(curNode.right);
if (curNode.left !== null) helperStack.push(curNode.left);
} else {
curNode = helperStack.pop()!;
res.push(curNode.val);
}
}
return res;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
# Scala
// Preorder traversal
object Solution {
import scala.collection.mutable
def preorderTraversal(root: TreeNode): List[Int] = {
val res = mutable.ListBuffer[Int]()
val stack = mutable.Stack[TreeNode]()
if (root != null) stack.push(root)
while (!stack.isEmpty) {
var curNode = stack.top
if (curNode != null) {
stack.pop()
if (curNode.right != null) stack.push(curNode.right)
if (curNode.left != null) stack.push(curNode.left)
stack.push(curNode)
stack.push(null)
} else {
stack.pop()
res.append(stack.pop().value)
}
}
res.toList
}
}
// Inorder traversal
object Solution {
import scala.collection.mutable
def inorderTraversal(root: TreeNode): List[Int] = {
val res = mutable.ListBuffer[Int]()
val stack = mutable.Stack[TreeNode]()
if (root != null) stack.push(root)
while (!stack.isEmpty) {
var curNode = stack.top
if (curNode != null) {
stack.pop()
if (curNode.right != null) stack.push(curNode.right)
stack.push(curNode)
stack.push(null)
if (curNode.left != null) stack.push(curNode.left)
} else {
stack.pop()
res.append(stack.pop().value)
}
}
res.toList
}
}
// Postorder traversal
object Solution {
import scala.collection.mutable
def postorderTraversal(root: TreeNode): List[Int] = {
val res = mutable.ListBuffer[Int]()
val stack = mutable.Stack[TreeNode]()
if (root != null) stack.push(root)
while (!stack.isEmpty) {
var curNode = stack.top
if (curNode != null) {
stack.pop()
stack.push(curNode)
stack.push(null)
if (curNode.right != null) stack.push(curNode.right)
if (curNode.left != null) stack.push(curNode.left)
} else {
stack.pop()
res.append(stack.pop().value)
}
}
res.toList
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
# Rust:
impl Solution{
// Preorder
pub fn preorder_traversal(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<i32> {
let mut res = vec![];
let mut stack = vec![];
if root.is_some(){
stack.push(root);
}
while !stack.is_empty(){
if let Some(node) = stack.pop().unwrap(){
if node.borrow().right.is_some(){
stack.push(node.borrow().right.clone());
}
if node.borrow().left.is_some(){
stack.push(node.borrow().left.clone());
}
stack.push(Some(node));
stack.push(None);
}else{
res.push(stack.pop().unwrap().unwrap().borrow().val);
}
}
res
}
// Inorder
pub fn inorder_traversal(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<i32> {
let mut res = vec![];
let mut stack = vec![];
if root.is_some() {
stack.push(root);
}
while !stack.is_empty() {
if let Some(node) = stack.pop().unwrap() {
if node.borrow().right.is_some() {
stack.push(node.borrow().right.clone());
}
stack.push(Some(node.clone()));
stack.push(None);
if node.borrow().left.is_some() {
stack.push(node.borrow().left.clone());
}
} else {
res.push(stack.pop().unwrap().unwrap().borrow().val);
}
}
res
}
// Postorder
pub fn postorder_traversal(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<i32> {
let mut res = vec![];
let mut stack = vec![];
if root.is_some() {
stack.push(root);
}
while !stack.is_empty() {
if let Some(node) = stack.pop().unwrap() {
stack.push(Some(node.clone()));
stack.push(None);
if node.borrow().right.is_some() {
stack.push(node.borrow().right.clone());
}
if node.borrow().left.is_some() {
stack.push(node.borrow().left.clone());
}
} else {
res.push(stack.pop().unwrap().unwrap().borrow().val);
}
}
res
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
# C#
// Preorder traversal
public IList<int> PreorderTraversal(TreeNode root)
{
var res = new List<int>();
var st = new Stack<TreeNode>();
if (root == null) return res;
st.Push(root);
while (st.Count != 0)
{
var node = st.Peek();
if (node == null)
{
st.Pop();
node = st.Peek();
st.Pop();
res.Add(node.val);
}
else
{
st.Pop();
if (node.right != null) st.Push(node.right);
if (node.left != null) st.Push(node.left);
st.Push(node);
st.Push(null);
}
}
return res;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
// Inorder traversal
public IList<int> InorderTraversal(TreeNode root)
{
var res = new List<int>();
var st = new Stack<TreeNode>();
if (root == null) return res;
st.Push(root);
while (st.Count != 0)
{
var node = st.Peek();
if (node == null)
{
st.Pop();
node = st.Peek();
st.Pop();
res.Add(node.val);
}
else
{
st.Pop();
if (node.right != null) st.Push(node.right);
st.Push(node);
st.Push(null);
if (node.left != null) st.Push(node.left);
}
}
return res;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
// Postorder traversal
public IList<int> PostorderTraversal(TreeNode root)
{
var res = new List<int>();
var st = new Stack<TreeNode>();
if (root == null) return res;
st.Push(root);
while (st.Count != 0)
{
var node = st.Peek();
if (node == null)
{
st.Pop();
node = st.Peek();
st.Pop();
res.Add(node.val);
}
else
{
st.Pop();
if (node.left != null) st.Push(node.left);
if (node.right != null) st.Push(node.right);
st.Push(node);
st.Push(null);
}
}
res.Reverse(0, res.Count);
return res;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
