501. Mode in Binary Search Tree

LeetCode problem link (opens new window)

Given a binary search tree (BST) with duplicates, find all the modes (elements with the highest frequency) in the BST.

Assume the BST is defined as follows:

• The value of nodes in the left subtree is less than or equal to the value of the current node
• The value of nodes in the right subtree is greater than or equal to the value of the current node
• Both the left and right subtrees are binary search trees

Example:

Given BST [1,null,2,2],

Return [2].

Note: If the mode is more than one, output order does not matter.

Follow up: Could you do that without using any extra space? (Assuming the implicit stack space generated by the recursion does not count).

Approach

This problem has a recursive approach that I will explain from two perspectives.

First, let's consider how to solve it if it's not a binary search tree. Then, we'll see how the BST property can be leveraged to solve the problem differently. Comparing the two methods can deepen your understanding of binary trees.

Recursive Approach

If it's not a binary search tree

For a general binary tree, the most straightforward method is to traverse the tree, use a map to count frequencies, sort the frequencies, and then choose the elements with the highest frequencies.

Specific steps are as follows:

1. Traverse the entire tree and use a map to count frequency

The traversal order doesn't matter since you need to cover the entire tree. Preorder, inorder, postorder, and even level-order traversal will work. Here we use preorder traversal with the following code:

// Map<int, int> key: element, value: frequency
void searchBST(TreeNode* cur, unordered_map<int, int>& map) { // Preorder traversal
    if (cur == NULL) return;
    map[cur->val]++; // Count element frequency
    searchBST(cur->left, map);
    searchBST(cur->right, map);
    return;
}

2. Sort the frequencies stored in the map

You cannot sort values directly in a map using C++ standard library features if you’re using std::map or std::multimap. Thus, convert the map to a vector, which also stores pair<int, int> where the first int is the element and the second int is the frequency.

bool static cmp (const pair<int, int>& a, const pair<int, int>& b) {
    return a.second > b.second; // Sort frequencies in descending order
}

vector<pair<int, int>> vec(map.begin(), map.end());
sort(vec.begin(), vec.end(), cmp); // Sort by frequency

3. Pick the elements with the highest frequency

The vector contains pairs sorted by frequency; now you can choose elements with the highest frequency:

result.push_back(vec[0].first);
for (int i = 1; i < vec.size(); i++) {
    if (vec[i].second == vec[0].second) result.push_back(vec[i].first);
    else break;
}
return result;

The whole C++ code is as follows:

class Solution {
private:

void searchBST(TreeNode* cur, unordered_map<int, int>& map) {
    if (cur == NULL) return;
    map[cur->val]++;
    searchBST(cur->left, map);
    searchBST(cur->right, map);
    return;
}
bool static cmp (const pair<int, int>& a, const pair<int, int>& b) {
    return a.second > b.second;
}
public:
    vector<int> findMode(TreeNode* root) {
        unordered_map<int, int> map;
        vector<int> result;
        if (root == NULL) return result;
        searchBST(root, map);
        vector<pair<int, int>> vec(map.begin(), map.end());
        sort(vec.begin(), vec.end(), cmp);
        result.push_back(vec[0].first);
        for (int i = 1; i < vec.size(); i++) {
            if (vec[i].second == vec[0].second) result.push_back(vec[i].first);
            else break;
        }
        return result;
    }
};

If the problem didn’t specify that the tree is a binary search tree, you would solve it using the above logic!

If it is a binary search tree

Since it's a binary search tree, its inorder traversal is sorted.

For example:

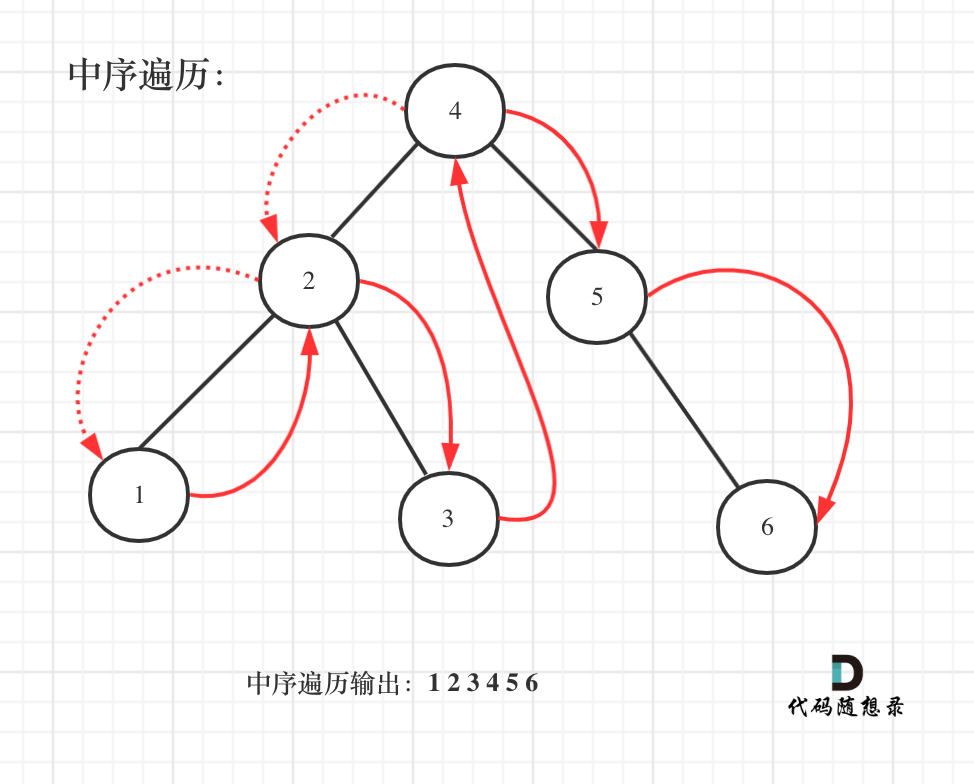
Inorder traversal code is as follows:

void searchBST(TreeNode* cur) {
    if (cur == NULL) return;
    searchBST(cur->left);
    (process the node)
    searchBST(cur->right);
    return;
}

When traversing a sorted array for mode, you compare consecutive elements and keep a collection of the most frequent elements.

The problem is, in a binary tree, how can this be managed efficiently?

One approach is to have a pointer pointing to the previous node, allowing the current node (cur) to be compared with the pre (previous node).

Initially, set pre = NULL to recognize the first element.

if (pre == NULL) { // First node
    count = 1; // Frequency is 1
} else if (pre->val == cur->val) { // Same as previous node
    count++;
} else { // Different from the previous node
    count = 1;
}
pre = cur; // Update the previous node

If count equals maxCount, you should add this element to the result vector. If count is greater than maxCount, update maxCount and clear the result vector.

if (count == maxCount) { 
    result.push_back(cur->val);
}

if (count > maxCount) {
    maxCount = count; 
    result.clear();     
    result.push_back(cur->val);
}

The complete code is below: (You can get all modes with a single tree traversal.)

class Solution {
private:
    int maxCount = 0;
    int count = 0;
    TreeNode* pre = NULL;
    vector<int> result;
    void searchBST(TreeNode* cur) {
        if (cur == NULL) return;

        searchBST(cur->left);
        
        if (pre == NULL) {
            count = 1;
        } else if (pre->val == cur->val) {
            count++;
        } else {
            count = 1;
        }
        pre = cur;

        if (count == maxCount) {
            result.push_back(cur->val);
        }

        if (count > maxCount) {
            maxCount = count;
            result.clear();
            result.push_back(cur->val);
        }

        searchBST(cur->right);
        return;
    }

public:
    vector<int> findMode(TreeNode* root) {
        count = 0;
        maxCount = 0;
        pre = NULL;
        result.clear();

        searchBST(root);
        return result;
    }
};

Iterative Approach

The code logic is the same; we just use an iterative inorder traversal:

Refer to:

• Binary Tree Iterative Traversal (opens new window)
• Unified Iterative Traversal of Binary Tree (opens new window)

The following is one way to do an inorder traversal iteratively, maintaining the logic:

class Solution {
public:
    vector<int> findMode(TreeNode* root) {
        stack<TreeNode*> st;
        TreeNode* cur = root;
        TreeNode* pre = NULL;
        int maxCount = 0;
        int count = 0;
        vector<int> result;
        while (cur != NULL || !st.empty()) {
            if (cur != NULL) {
                st.push(cur);
                cur = cur->left;
            } else {
                cur = st.top();
                st.pop();
                if (pre == NULL) {
                    count = 1;
                } else if (pre->val == cur->val) {
                    count++;
                } else {
                    count = 1;
                }
                if (count == maxCount) {
                    result.push_back(cur->val);
                }

                if (count > maxCount) {
                    maxCount = count;
                    result.clear();
                    result.push_back(cur->val);
                }
                pre = cur;
                cur = cur->right;
            }
        }
        return result;
    }
};

Conclusion

In the recursive approach, I've shown how to solve for modes in a general binary tree context. Then I introduced how to leverage the binary search tree property to find modes efficiently, enhancing binary tree understanding.

When traversing the binary search tree, I introduced a technique to find the most frequent elements in one pass, instead of traversing the tree twice. If the task was simpler and required a single mode, one pass would suffice.

Finally, I provided a corresponding iterative approach by adding the central node processing logic.

Identifying the mode in a binary search tree is a simple problem, but understanding the approach deeply can be quite enlightening when learning binary trees.