# 450. Delete Node in a BST
Link to the problem on LeetCode (opens new window)
Given a root node of a binary search tree and a key, delete the node in the BST with that key and return the root node of the updated BST. Ensure that the properties of the BST remain unchanged.
Generally, deletion can be broken down into two steps:
- Find the node to be deleted;
- If the node is found, delete it.
Note: The time complexity requirement is $O(h)$, where h is the height of the tree.
Example:

# Approach
Deleting a node in a search tree is more complex than adding a node, with numerous cases to consider.
# Recursive Approach
Three key steps for recursion:
- Define the parameters and return value of the recursive function
For the return value of the recursive function, in 0701.Insert into a Binary Search Tree (opens new window) we used a return value to add a new node, and here we can use a return value to delete a node.
Here is the function signature:
TreeNode* deleteNode(TreeNode* root, int key)
- Define the termination condition
Return when encountering a null node, which indicates the node to be deleted was not found.
if (root == nullptr) return root;
- Define the logic of a single recursion step
There are several cases to handle when deleting a node in a binary search tree. Be prepared for these:
- The first case: If the node to be deleted is not found, return upon reaching a null node.
- If the node to be deleted is found:
- Second case: If both children are null (leaf node), delete the node and return
NULLas the root node. - Third case: If the left child is null and the right child is not, delete the node and return the right child as the root node.
- Fourth case: If the right child is null and the left child is not, delete the node and return the left child as the root node.
- Fifth case: If both children are not null, move the root of the left subtree to the leftmost node of the right subtree. Return the right child as the new root node.
- Second case: If both children are null (leaf node), delete the node and return
The following diagram illustrates the fifth case:
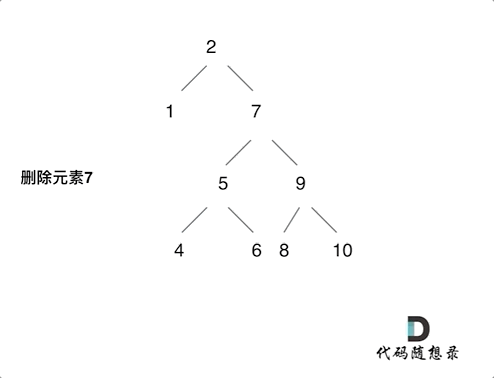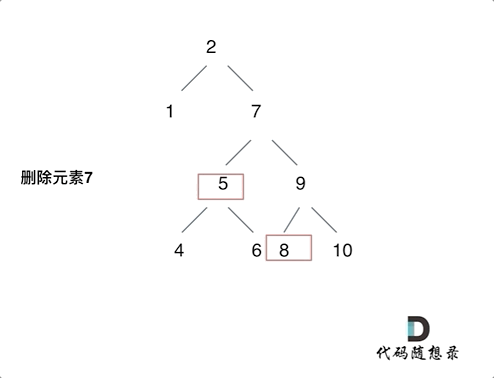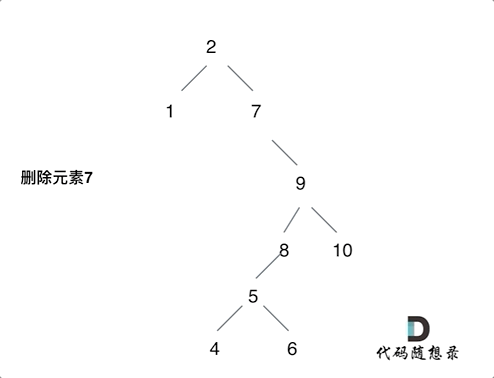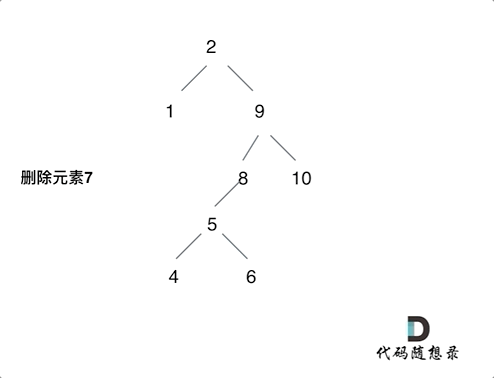
The tree illustration shows the deletion of element 7. We move the root of the left subtree (element 5) to the leftmost position of the right subtree (element 8), with element 9 as the new root.
Try to draw a diagram yourself to better understand this deletion logic.
Here's the code implementing this:
if (root->val == key) {
if (root->left == nullptr) return root->right;
else if (root->right == nullptr) return root->left;
else {
TreeNode* cur = root->right;
while(cur->left != nullptr) {
cur = cur->left;
}
cur->left = root->left;
TreeNode* tmp = root;
root = root->right;
delete tmp;
return root;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
The updated node is returned to the previous level using root->left or root->right to catch it, as shown here:
if (root->val > key) root->left = deleteNode(root->left, key);
if (root->val < key) root->right = deleteNode(root->right, key);
return root;
2
3
Full implementation:
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
if (root == nullptr) return root;
if (root->val == key) {
if (root->left == nullptr && root->right == nullptr) {
delete root;
return nullptr;
} else if (root->left == nullptr) {
auto retNode = root->right;
delete root;
return retNode;
} else if (root->right == nullptr) {
auto retNode = root->left;
delete root;
return retNode;
} else {
TreeNode* cur = root->right;
while(cur->left != nullptr) {
cur = cur->left;
}
cur->left = root->left;
TreeNode* tmp = root;
root = root->right;
delete tmp;
return root;
}
}
if (root->val > key) root->left = deleteNode(root->left, key);
if (root->val < key) root->right = deleteNode(root->right, key);
return root;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# Deleting in a General Binary Tree
Here we introduce a general deletion method for binary trees without using the properties of a search tree, by swapping values to delete the target node.
The target node is operated on twice:
- Swap the target node with the leftmost node of the right subtree.
- Overwrite it directly with
NULL.
Draw a diagram to better understand this.
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
if (root == nullptr) return root;
if (root->val == key) {
if (root->right == nullptr) {
return root->left;
}
TreeNode *cur = root->right;
while (cur->left) {
cur = cur->left;
}
swap(root->val, cur->val);
}
root->left = deleteNode(root->left, key);
root->right = deleteNode(root->right, key);
return root;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Although shorter, the recursive approach is recommended for its clarity.
# Iterative Approach
The iterative approach is more complex, but follows the same logic of manipulating the node structure. A pointer pre is used to track the parent node, assisting in deletion.
class Solution {
private:
TreeNode* deleteOneNode(TreeNode* target) {
if (target == nullptr) return target;
if (target->right == nullptr) return target->left;
TreeNode* cur = target->right;
while (cur->left) {
cur = cur->left;
}
cur->left = target->left;
return target->right;
}
public:
TreeNode* deleteNode(TreeNode* root, int key) {
if (root == nullptr) return root;
TreeNode* cur = root;
TreeNode* pre = nullptr;
while (cur) {
if (cur->val == key) break;
pre = cur;
if (cur->val > key) cur = cur->left;
else cur = cur->right;
}
if (pre == nullptr) {
return deleteOneNode(cur);
}
if (pre->left && pre->left->val == key) {
pre.left = deleteOneNode(cur);
}
if (pre.right && pre->right->val == key) {
pre.right = deleteOneNode(cur);
}
return root;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
# Summary
Deleting a node in a binary search tree is significantly more complex than inserting one. Adding a node simply involves placing it at a leaf, whereas deleting a node may necessitate structural adjustments.
Using the recursive function's return value, we effectively remove a node from the binary tree. Pay special attention to the fifth case.
For beginners, focusing on mastering the first recursive method is recommended.
# Other Languages Versions
# Java
// Version 1 (Most comprehensible)
class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
if (root == null) return root;
if (root.val == key) {
if (root.left == null) {
return root.right;
} else if (root.right == null) {
return root.left;
} else {
TreeNode cur = root.right;
while (cur.left != null) {
cur = cur.left;
}
cur.left = root.left;
root = root.right;
return root;
}
}
if (root.val > key) root.left = deleteNode(root.left, key);
if (root.val < key) root.right = deleteNode(root.right, key);
return root;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
root = delete(root,key);
return root;
}
private TreeNode delete(TreeNode root, int key) {
if (root == null) return null;
if (root.val > key) {
root.left = delete(root.left,key);
} else if (root.val < key) {
root.right = delete(root.right,key);
} else {
if (root.left == null) return root.right;
if (root.right == null) return root.left;
TreeNode tmp = root.right;
while (tmp.left != null) {
tmp = tmp.left;
}
root.val = tmp.val;
root.right = delete(root.right,tmp.val);
}
return root;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
Recursive
class Solution {
public TreeNode deleteNode(TreeNode root, int key) {
if (root == null){
return null;
}
TreeNode cur = root;
TreeNode pre = null;
while (cur != null){
if (cur.val < key){
pre = cur;
cur = cur.right;
} else if (cur.val > key) {
pre = cur;
cur = cur.left;
}else {
break;
}
}
if (pre == null){
return deleteOneNode(cur);
}
if (pre.left !=null && pre.left.val == key){
pre.left = deleteOneNode(cur);
}
if (pre.right !=null && pre.right.val == key){
pre.right = deleteOneNode(cur);
}
return root;
}
public TreeNode deleteOneNode(TreeNode node){
if (node == null){
return null;
}
if (node.right == null){
return node.left;
}
TreeNode cur = node.right;
while (cur.left !=null){
cur = cur.left;
}
cur.left = node.left;
return node.right;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
# Python
Recursive (Version 1)
class Solution:
def deleteNode(self, root, key):
if root is None:
return root
if root.val == key:
if root.left is None and root.right is None:
return None
elif root.left is None:
return root.right
elif root.right is None:
return root.left
else:
cur = root.right
while cur.left is not None:
cur = cur.left
cur.left = root.left
return root.right
if root.val > key:
root.left = self.deleteNode(root.left, key)
if root.val < key:
root.right = self.deleteNode(root.right, key)
return root
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Recursive (Version 2)
class Solution:
def deleteNode(self, root, key):
if root is None:
return None
if root.val == key:
if root.right is None:
return root.left
cur = root.right
while cur.left:
cur = cur.left
cur.left = root.left
return root.right
if root.val > key:
root.left = self.deleteNode(root.left, key)
if root.val < key:
root.right = self.deleteNode(root.right, key)
return root
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Iterative
class Solution:
def deleteOneNode(self, target: TreeNode) -> TreeNode:
if target is None:
return target
if target.right is None:
return target.left
cur = target.right
while cur.left:
cur = cur.left
cur.left = target.left
return target.right
def deleteNode(self, root: TreeNode, key: int) -> TreeNode:
if root is None:
return root
cur = root
pre = None
while cur:
if cur.val == key: break
pre = cur
if cur.val > key:
cur = cur.left
else:
cur = cur.right
if pre is None:
return self.deleteOneNode(cur)
if pre.left and pre.left.val == key:
pre.left = self.deleteOneNode(cur)
if pre.right and pre.right.val == key:
pre.right = self.deleteOneNode(cur)
return root
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# Go
// Recursive version
func deleteNode(root *TreeNode, key int) *TreeNode {
if root == nil {
return nil
}
if key < root.Val {
root.Left = deleteNode(root.Left, key)
return root
}
if key > root.Val {
root.Right = deleteNode(root.Right, key)
return root
}
if root.Right == nil {
return root.Left
}
if root.Left == nil{
return root.Right
}
minnode := root.Right
for minnode.Left != nil {
minnode = minnode.Left
}
root.Val = minnode.Val
root.Right = deleteNode1(root.Right)
return root
}
func deleteNode1(root *TreeNode) *TreeNode {
if root.Left == nil {
pRight := root.Right
root.Right = nil
return pRight
}
root.Left = deleteNode1(root.Left)
return root
}
// Iterative version
func deleteNode(root *TreeNode, key int) *TreeNode {
deleteOneNode := func(target *TreeNode) *TreeNode {
if target == nil {
return target
}
if target.Right == nil {
return target.Left
}
cur := target.Right
for cur.Left != nil {
cur = cur.Left
}
cur.Left = target.Left
return target.Right
}
if root == nil {
return root
}
var pre *TreeNode
cur := root
for cur != nil {
if cur.Val == key {
break
}
pre = cur
if cur.Val > key {
cur = cur.Left
} else {
cur = cur.Right
}
}
if pre == nil {
return deleteOneNode(cur)
}
if pre.Left != nil && pre.Left.Val == key {
pre.Left = deleteOneNode(cur)
}
if pre.Right != nil && pre.Right.Val == key {
pre.Right = deleteOneNode(cur)
}
return root
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
# JavaScript
Recursive
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @param {number} key
* @return {TreeNode}
*/
var deleteNode = function(root, key) {
if (!root) return null;
if (key > root.val) {
root.right = deleteNode(root.right, key);
return root;
} else if (key < root.val) {
root.left = deleteNode(root.left, key);
return root;
} else {
if (!root.left && !root.right) {
return null
}
if (root.left && !root.right) {
return root.left;
} else if (root.right && !root.left) {
return root.right;
}
const rightNode = root.right;
const minNode = getMinNode(rightNode);
root.val = minNode.val;
root.right = deleteNode(root.right, minNode.val);
return root;
}
};
function getMinNode(root) {
while (root.left) {
root = root.left;
}
return root;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
Iterative
var deleteNode = function (root, key) {
const deleteOneNode = target => {
if (!target) return target
if (!target.right) return target.left
let cur = target.right
while (cur.left) {
cur = cur.left
}
cur.left = target.left
return target.right
}
if (!root) return root
let cur = root
let pre = null
while (cur) {
if (cur.val === key) break
pre = cur
cur.val > key ? cur = cur.left : cur = cur.right
}
if (!pre) {
return deleteOneNode(cur)
}
if (pre.left && pre.left.val === key) {
pre.left = deleteOneNode(cur)
}
if (pre.right && pre.right.val === key) {
pre.right = deleteOneNode(cur)
}
return root
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# TypeScript
Recursive approach:
function deleteNode(root: TreeNode | null, key: number): TreeNode | null {
if (root === null) return null;
if (root.val === key) {
if (root.left === null && root.right === null) return null;
if (root.left === null) return root.right;
if (root.right === null) return root.left;
let curNode: TreeNode = root.right;
while (curNode.left !== null) {
curNode = curNode.left;
}
curNode.left = root.left;
return root.right;
}
if (root.val > key) root.left = deleteNode(root.left, key);
if (root.val < key) root.right = deleteNode(root.right, key);
return root;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Iterative approach:
function deleteNode(root: TreeNode | null, key: number): TreeNode | null {
function removeTargetNode(root: TreeNode): TreeNode | null {
if (root.left === null && root.right === null) return null;
if (root.right === null) return root.left;
if (root.left === null) return root.right;
let curNode: TreeNode | null = root.right;
while (curNode.left !== null) {
curNode = curNode.left;
}
curNode.left = root.left;
return root.right;
}
let preNode: TreeNode | null = null,
curNode: TreeNode | null = root;
while (curNode !== null) {
if (curNode.val === key) break;
preNode = curNode;
if (curNode.val > key) {
curNode = curNode.left;
} else {
curNode = curNode.right;
}
}
if (curNode === null) return root;
if (preNode === null) {
return removeTargetNode(curNode);
}
if (preNode.val > key) {
preNode.left = removeTargetNode(curNode);
} else {
preNode.right = removeTargetNode(curNode);
}
return root;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
# Scala
object Solution {
def deleteNode(root: TreeNode, key: Int): TreeNode = {
if (root == null) return root
if (root.value == key) {
if (root.left == null && root.right == null) return null
else if (root.left == null && root.right != null) return root.right
else if (root.left != null && root.right == null) return root.left
else {
var tmp = root.right
while (tmp.left != null) tmp = tmp.left
tmp.left = root.left
return root.right
}
}
if (root.value > key) root.left = deleteNode(root.left, key)
if (root.value < key) root.right = deleteNode(root.right, key)
root
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# Rust
impl Solution {
pub fn delete_node(
root: Option<Rc<RefCell<TreeNode>>>,
key: i32,
) -> Option<Rc<RefCell<TreeNode>>> {
root.as_ref()?;
let mut node = root.as_ref().unwrap().borrow_mut();
match node.val.cmp(&key) {
std::cmp::Ordering::Less => node.right = Self::delete_node(node.right.clone(), key),
std::cmp::Ordering::Equal => match (node.left.clone(), node.right.clone()) {
(None, None) => return None,
(None, Some(r)) => return Some(r),
(Some(l), None) => return Some(l),
(Some(l), Some(r)) => {
let mut cur = Some(r.clone());
while let Some(n) = cur.clone().unwrap().borrow().left.clone() {
cur = Some(n);
}
cur.unwrap().borrow_mut().left = Some(l);
return Some(r);
}
},
std::cmp::Ordering::Greater => node.left = Self::delete_node(node.left.clone(), key),
}
drop(node);
root
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# C#
Recursive approach:
public TreeNode DeleteNode(TreeNode root, int key) {
if (root == null) return null;
if(key == root.val) {
if(root.left == null && root.right == null) return null;
if (root.left == null && root.right != null) return root.right;
if (root.left != null && root.right == null) return root.left;
if(root.left != null && root.right != null) {
TreeNode leftNode = root.right;
while(leftNode.left != null)
leftNode = leftNode.left;
leftNode.left = root.left;
return root.right;
}
}
if(root.val > key) root.left = DeleteNode(root.left, key);
if(root.val < key) root.right = DeleteNode(root.right, key);
return root;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# Ruby
Recursive approach:
# @param {TreeNode} root
# @param {Integer} key
# @return {TreeNode}
def delete_node(root, key)
return nil if root.nil?
right = root.right
left = root.left
if root.val == key
return right if left.nil?
return left if right.nil?
node = right
while node.left
node = node.left
end
node.left = left
return right
end
if root.val > key
root.left = delete_node(left, key)
else
root.right = delete_node(right, key)
end
return root
end
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
