Are you seeking height or depth, have you figured it out?
# 110. Balanced Binary Tree
LeetCode Problem Link (opens new window)
Given a binary tree, determine if it is height-balanced.
For this problem, a height-balanced binary tree is defined as a binary tree in which the height of the two subtrees of every node never differ by more than 1.
Example 1:
Given the binary tree [3,9,20,null,null,15,7]

Returns true.
Example 2:
Given the binary tree [1,2,2,3,3,null,null,4,4]

Returns false.
# Additional Information
At first glance, this problem seems quite similar to 0104.Maximum Depth of Binary Tree (opens new window), but there are significant differences.
Let's clarify some concepts:
- The depth of a binary tree node: The number of edges on the longest simple path from the root node to the node.
- The height of a binary tree node: The number of edges on the longest simple path from the node to a leaf node.
However, in LeetCode, the emphasis on depth and height clearly indicates counting by nodes, as shown in the diagram:
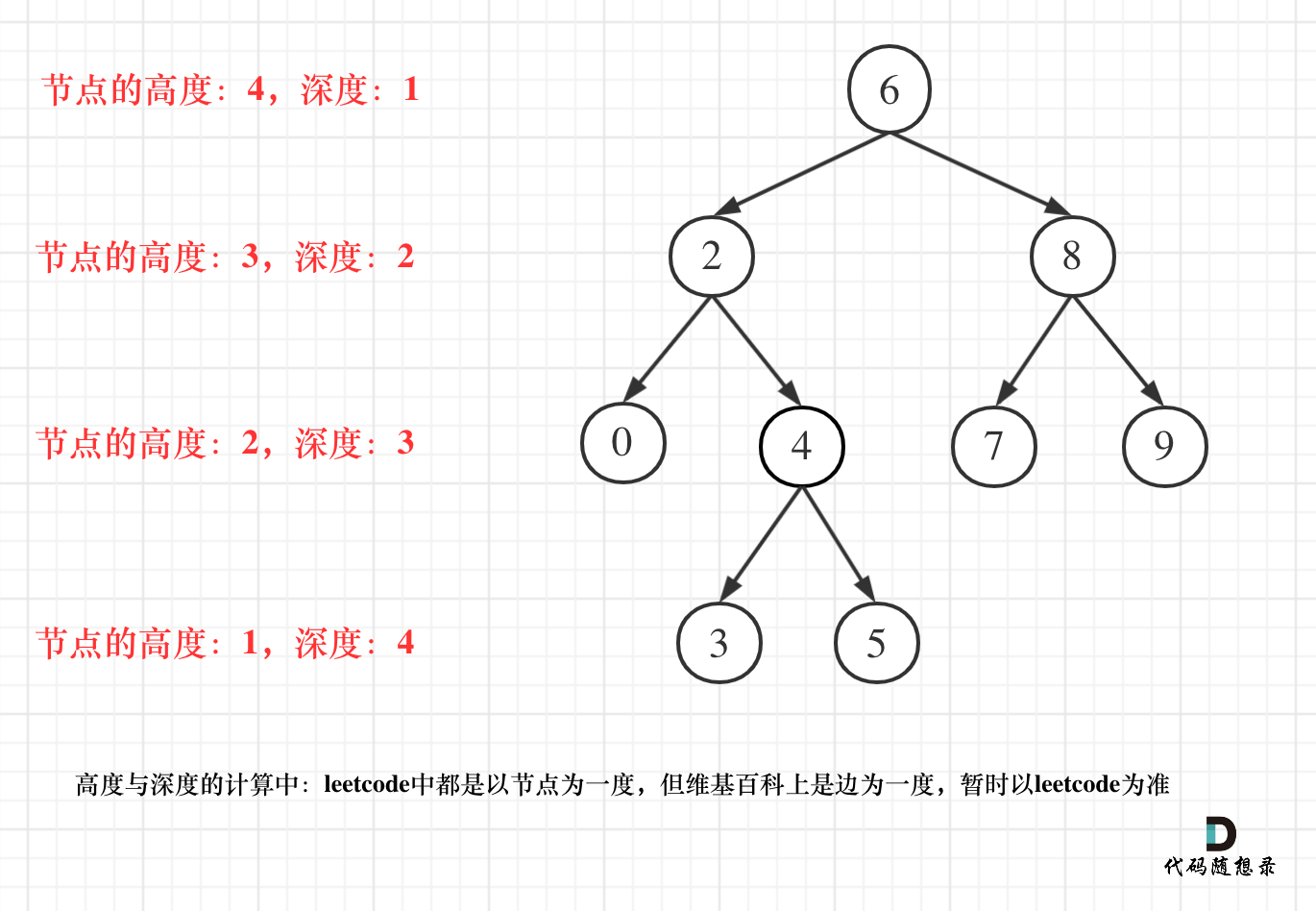
Regarding whether the depth of the root node is 1 or 0, different sources have different standards. In LeetCode, all problems use nodes as a unit (i.e., the depth of the root node is 1). However, Wikipedia defines it using edges as a unit (i.e., the depth of the root node is 0). We shall align with LeetCode (since we're solving problems on this platform).
Depth can be accounted for from top to bottom, so it requires pre-order traversal (Node-Left-Right), while height can only be determined from bottom to top, necessitating post-order traversal (Left-Right-Node).
Some might wonder why in 0104.Maximum Depth of Binary Tree (opens new window), where we are seeking the maximum depth of a binary tree, we also use post-order traversal.
This is because the logic of the code actually derives the height of the root node, and the height of the root node is the maximum depth of the tree, which is why post-order traversal works.
In 0104.Maximum Depth of Binary Tree (opens new window), if genuinely determining the maximum depth of a binary tree, the code could be written as follows (using pre-order traversal):
class Solution {
public:
int result;
void getDepth(TreeNode* node, int depth) {
result = depth > result ? depth : result; // Node
if (node->left == NULL && node->right == NULL) return;
if (node->left) { // Left
depth++; // Increase depth
getDepth(node->left, depth);
depth--; // Backtrack, decrease depth
}
if (node->right) { // Right
depth++; // Increase depth
getDepth(node->right, depth);
depth--; // Backtrack, decrease depth
}
return;
}
int maxDepth(TreeNode* root) {
result = 0;
if (root == NULL) return result;
getDepth(root, 1);
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
From this, you can see that pre-order traversal (Node-Left-Right) is used, which is the genuine logic for getting depth!
The simplified version of the above code is as follows:
class Solution {
public:
int result;
void getDepth(TreeNode* node, int depth) {
result = depth > result ? depth : result; // Node
if (node->left == NULL && node->right == NULL) return;
if (node->left) { // Left
getDepth(node->left, depth + 1);
}
if (node->right) { // Right
getDepth(node->right, depth + 1);
}
return;
}
int maxDepth(TreeNode* root) {
result = 0;
if (root == 0) return result;
getDepth(root, 1);
return result;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# Solution Approach
# Recursion
By now, everyone should understand that since we need to compare heights, we must use post-order traversal.
Analysis of the three steps of recursion:
- Clarify the parameters and return value of the recursive function:
Parameters: The currently passed-in node. Return value: The height of the tree with the currently passed-in node as the root node.
How to mark whether the left and right subtrees' height difference exceeds 1?
If the tree with the current node as the root node is no longer a balanced binary tree, returning the height would be meaningless.
Therefore, you can return -1 to mark that it no longer meets the criteria of a balanced tree.
Here is the code:
int getHeight(TreeNode* node)
// -1 indicates it is no longer a balanced binary tree; otherwise, the return value is the height of the tree rooted at the node
2
- Clarify the termination condition
The termination condition remains encountering a null node, returning 0, indicating the height of the sub-tree rooted at the current node is 0.
Here is the code:
if (node == NULL) {
return 0;
}
2
3
- Clarify the logic of a single-level recursion
How to determine if the tree with the currently passed-in node as root is balanced? Of course, by observing the height difference between its left and right subtrees.
Find the heights of its left and right subtrees respectively, and if the difference is less than or equal to 1, return the height of the current tree; otherwise return -1, marking it as no longer a balanced binary tree.
Here is the code:
int leftHeight = getHeight(node->left); // Left
if (leftHeight == -1) return -1;
int rightHeight = getHeight(node->right); // Right
if (rightHeight == -1) return -1;
int result;
if (abs(leftHeight - rightHeight) > 1) { // Node
result = -1;
} else {
result = 1 + max(leftHeight, rightHeight); // The maximum height of the tree with the current node as root
}
return result;
2
3
4
5
6
7
8
9
10
11
12
13
After simplifying, the code is as follows:
int leftHeight = getHeight(node->left);
if (leftHeight == -1) return -1;
int rightHeight = getHeight(node->right);
if (rightHeight == -1) return -1;
return abs(leftHeight - rightHeight) > 1 ? -1 : 1 + max(leftHeight, rightHeight);
2
3
4
5
At this point, the recursive function has been written, which takes a node pointer and returns the tree height rooted at the node. If it is not a balanced binary tree, it returns -1.
The whole getHeight code is as follows:
int getHeight(TreeNode* node) {
if (node == NULL) {
return 0;
}
int leftHeight = getHeight(node->left);
if (leftHeight == -1) return -1;
int rightHeight = getHeight(node->right);
if (rightHeight == -1) return -1;
return abs(leftHeight - rightHeight) > 1 ? -1 : 1 + max(leftHeight, rightHeight);
}
2
3
4
5
6
7
8
9
10
Here's the entire code for recursion in this problem:
class Solution {
public:
// Returns the height of the binary tree rooted at the node; if it is no longer a balanced tree, return -1
int getHeight(TreeNode* node) {
if (node == NULL) {
return 0;
}
int leftHeight = getHeight(node->left);
if (leftHeight == -1) return -1;
int rightHeight = getHeight(node->right);
if (rightHeight == -1) return -1;
return abs(leftHeight - rightHeight) > 1 ? -1 : 1 + max(leftHeight, rightHeight);
}
bool isBalanced(TreeNode* root) {
return getHeight(root) == -1 ? false : true;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# Iteration
In 0104.Maximum Depth of Binary Tree (opens new window), we can use level-order traversal to determine depth, but we cannot directly use level-order traversal to determine height, highlighting the difference between finding depth and height.
The iterative method in this problem can define a function, designed specifically to determine height.
This function uses a stack to simulate post-order traversal to find the height of each node (actually by finding the maximum depth of the subtree rooted at the input node).
The code is as follows:
int getDepth(TreeNode* cur) {
stack<TreeNode*> st;
if (cur != NULL) st.push(cur);
int depth = 0; // Records depth
int result = 0;
while (!st.empty()) {
TreeNode* node = st.top();
if (node != NULL) {
st.pop();
st.push(node); // Node
st.push(NULL);
depth++;
if (node->right) st.push(node->right); // Right
if (node->left) st.push(node->left); // Left
} else {
st.pop();
node = st.top();
st.pop();
depth--;
}
result = result > depth ? result : depth;
}
return result;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
Then, use a stack to simulate post-order traversal, checking each node and determining if the heights of the left and right children meet the conditions:
bool isBalanced(TreeNode* root) {
stack<TreeNode*> st;
if (root == NULL) return true;
st.push(root);
while (!st.empty()) {
TreeNode* node = st.top(); // Node
st.pop();
if (abs(getDepth(node->left) - getDepth(node->right)) > 1) { // Determine if the height difference between the left and right children meets conditions
return false;
}
if (node->right) st.push(node->right); // Right (Do not push null nodes onto the stack)
if (node->left) st.push(node->left); // Left (Do not push null nodes onto the stack)
}
return true;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Here is the full code:
class Solution {
private:
int getDepth(TreeNode* cur) {
stack<TreeNode*> st;
if (cur != NULL) st.push(cur);
int depth = 0; // Records depth
int result = 0;
while (!st.empty()) {
TreeNode* node = st.top();
if (node != NULL) {
st.pop();
st.push(node); // Node
st.push(NULL);
depth++;
if (node->right) st.push(node->right); // Right
if (node->left) st.push(node->left); // Left
} else {
st.pop();
node = st.top();
st.pop();
depth--;
}
result = result > depth ? result : depth;
}
return result;
}
public:
bool isBalanced(TreeNode* root) {
stack<TreeNode*> st;
if (root == NULL) return true;
st.push(root);
while (!st.empty()) {
TreeNode* node = st.top(); // Node
st.pop();
if (abs(getDepth(node->left) - getDepth(node->right)) > 1) {
return false;
}
if (node->right) st.push(node->right); // Right (Do not push null nodes onto the stack)
if (node->left) st.push(node->left); // Left (Do not push null nodes onto the stack)
}
return true;
}
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
Using iteration for this problem is actually inefficient because it is not a good simulation of the backtracking process, leading to many repetitive calculations.
Even though, theoretically, all recursion can be achieved using iteration, some scenarios might be challenging.
For instance, albeit aware backtracking is essentially recursion, few people implement backtracking algorithms iteratively!
This is because backtracking algorithms are already complex recursive processes, and using iteration would be adding unnecessary complexity and might not even enhance efficiency.
# Conclusion
Through this problem, one understands the differences between finding the depth and height of a binary tree, with depth fitting pre-order traversal and height fitting post-order traversal.
Though the iterative method for this problem is slightly complex, having a conceptual understanding is beneficial, though writing it out isn't mandatory.
Mastery of the recursive approach is critical!
# Other Language Versions
# Java:
Recursive Method:
class Solution {
/**
* Recursive Method
*/
public boolean isBalanced(TreeNode root) {
return getHeight(root) != -1;
}
private int getHeight(TreeNode root) {
if (root == null) {
return 0;
}
int leftHeight = getHeight(root.left);
if (leftHeight == -1) {
return -1;
}
int rightHeight = getHeight(root.right);
if (rightHeight == -1) {
return -1;
}
// If the height difference between the left and right subtrees is greater than 1, return -1 indicating it is no longer a balanced tree
if (Math.abs(leftHeight - rightHeight) > 1) {
return -1;
}
return Math.max(leftHeight, rightHeight) + 1;
}
}
class Solution {
/**
* Iterative Method, with lower efficiency due to repetitive height calculations
* Time Complexity: O(n^2)
*/
public boolean isBalanced(TreeNode root) {
if (root == null) {
return true;
}
Stack<TreeNode> stack = new Stack<>();
TreeNode pre = null;
while (root != null || !stack.isEmpty()) {
while (root != null) {
stack.push(root);
root = root.left;
}
TreeNode inNode = stack.peek();
// Null right node or already traversed
if (inNode.right == null || inNode.right == pre) {
// Compare the height difference between left and right subtrees, output result
if (Math.abs(getHeight(inNode.left) - getHeight(inNode.right)) > 1) {
return false;
}
stack.pop();
pre = inNode;
root = null; // No more nodes to traverse under the current node
} else {
root = inNode.right; // Right node not yet traversed, traverse right node
}
}
return true;
}
/**
* Layered traversal to determine the node's height
*/
public int getHeight(TreeNode root) {
if (root == null) {
return 0;
}
Deque<TreeNode> deque = new LinkedList<>();
deque.offer(root);
int depth = 0;
while (!deque.isEmpty()) {
int size = deque.size();
depth++;
for (int i = 0; i < size; i++) {
TreeNode poll = deque.poll();
if (poll.left != null) {
deque.offer(poll.left);
}
if (poll.right != null) {
deque.offer(poll.right);
}
}
}
return depth;
}
}
class Solution {
/**
* Optimized Iterative Method: Improves the getHeight function in the brute-force iterative method by using TreeNode.val to store
* the current tree node's height, which avoids repetitive traversal.
* With this height-fetching algorithm, time complexity is reduced to O(1), lowering the total time complexity to O(n).
*/
public boolean isBalanced(TreeNode root) {
if (root == null) {
return true;
}
Stack<TreeNode> stack = new Stack<>();
TreeNode pre = null;
while (root != null || !stack.isEmpty()) {
while (root != null) {
stack.push(root);
root = root.left;
}
TreeNode inNode = stack.peek();
// Null right node or already traversed
if (inNode.right == null || inNode.right == pre) {
// Output
if (Math.abs(getHeight(inNode.left) - getHeight(inNode.right)) > 1) {
return false;
}
stack.pop();
pre = inNode;
root = null; // No more nodes to traverse under the current node
} else {
root = inNode.right; // Right node not yet traversed, traverse right node
}
}
return true;
}
/**
* Calculate node's height
*/
public int getHeight(TreeNode root) {
if (root == null) {
return 0;
}
int leftHeight = root.left != null ? root.left.val : 0;
int rightHeight = root.right != null ? root.right.val : 0;
int height = Math.max(leftHeight, rightHeight) + 1;
root.val = height; // Use TreeNode.val to store the current node's height
return height;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
# Python:
Recursive Method:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isBalanced(self, root: TreeNode) -> bool:
if self.get_height(root) != -1:
return True
else:
return False
def get_height(self, root: TreeNode) -> int:
# Base Case
if not root:
return 0
# Left
if (left_height := self.get_height(root.left)) == -1:
return -1
# Right
if (right_height := self.get_height(root.right)) == -1:
return -1
# Node
if abs(left_height - right_height) > 1:
return -1
else:
return 1 + max(left_height, right_height)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
Concise Version of Recursive Method:
class Solution:
def isBalanced(self, root: Optional[TreeNode]) -> bool:
return self.get_hight(root) != -1
def get_hight(self, node):
if not node:
return 0
left = self.get_hight(node.left)
right = self.get_hight(node.right)
if left == -1 or right == -1 or abs(left - right) > 1:
return -1
return max(left, right) + 1
2
3
4
5
6
7
8
9
10
11
Iterative Method:
class Solution:
def getDepth(self, cur):
st = []
if cur is not None:
st.append(cur)
depth = 0
result = 0
while st:
node = st[-1]
if node is not None:
st.pop()
st.append(node) # Node
st.append(None)
depth += 1
if node.right:
st.append(node.right) # Right
if node.left:
st.append(node.left) # Left
else:
node = st.pop()
st.pop()
depth -= 1
result = max(result, depth)
return result
def isBalanced(self, root):
st = []
if root is None:
return True
st.append(root)
while st:
node = st.pop() # Node
if abs(self.getDepth(node.left) - self.getDepth(node.right)) > 1:
return False
if node.right:
st.append(node.right) # Right (Do not push null nodes onto the stack)
if node.left:
st.append(node.left) # Left (Do not push null nodes onto the stack)
return True
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
Concise Version of Iterative Method:
class Solution:
def isBalanced(self, root: Optional[TreeNode]) -> bool:
if not root:
return True
height_map = {}
stack = [root]
while stack:
node = stack.pop()
if node:
stack.append(node) # Node
stack.append(None)
# Use an array for iteration, first pushing the right node, ensuring the left node pops first
if node.right: # Right
stack.append(node.right)
if node.left: # Left
stack.append(node.left)
else:
real_node = stack.pop()
left, right = height_map.get(real_node.left, 0), height_map.get(real_node.right, 0)
if abs(left - right) > 1:
return False
height_map[real_node] = 1 + max(left, right)
return True
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# Go:
Recursive Method
func isBalanced(root *TreeNode) bool {
h := getHeight(root)
if h == -1 {
return false
}
return true
}
// Returns -1 if the tree with the node as root cannot be a balanced tree anymore, otherwise returns the height
func getHeight(root *TreeNode) int {
if root == nil {
return 0
}
l, r := getHeight(root.Left), getHeight(root.Right)
if l == -1 || r == -1 {
return -1
}
if l - r > 1 || r - l > 1 {
return -1
}
return max(l, r) + 1
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
Iterative Method
func isBalanced(root *TreeNode) bool {
st := make([]*TreeNode, 0)
if root == nil {
return true
}
st = append(st, root)
for len(st) > 0 {
node := st[len(st)-1]
st = st[:len(st)-1]
if math.Abs(float64(getDepth(node.Left)) - float64(getDepth(node.Right))) > 1 {
return false
}
if node.Right != nil {
st = append(st, node.Right)
}
if node.Left != nil {
st = append(st, node.Left)
}
}
return true
}
func getDepth(cur *TreeNode) int {
st := make([]*TreeNode, 0)
if cur != nil {
st = append(st, cur)
}
depth := 0
result := 0
for len(st) > 0 {
node := st[len(st)-1]
if node != nil {
st = st[:len(st)-1]
st = append(st, node, nil)
depth++
if node.Right != nil {
st = append(st, node.Right)
}
if node.Left != nil {
st = append(st, node.Left)
}
} else {
st = st[:len(st)-1]
node = st[len(st)-1]
st = st[:len(st)-1]
depth--
}
if result < depth {
result = depth
}
}
return result
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
# JavaScript:
Recursive Method:
var isBalanced = function(root) {
// Use the recursive three-step process + post-order traversal (Left-Right-Node) to find if the height difference exceeds 1
// 1. Determine the parameters and return value of the recursive function
const getDepth = function(node) {
// 2. Determine the termination condition of the recursive function
if(node === null) return 0;
// 3. Determine single-level recursive logic
let leftDepth = getDepth(node.left); // Height of the left subtree
// Return -1 if the left subtree is not balanced
if(leftDepth === -1) return -1;
let rightDepth = getDepth(node.right); // Height of the right subtree
// Return -1 if the right subtree is not balanced
if(rightDepth === -1) return -1;
if(Math.abs(leftDepth - rightDepth) > 1) {
return -1;
} else {
return 1 + Math.max(leftDepth, rightDepth);
}
}
return !(getDepth(root) === -1);
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
Iterative Method:
// Get the current node's height
var getHeight = function (curNode) {
let queue = [];
if (curNode !== null) queue.push(curNode); // Pushes current node
let depth = 0, res = 0;
while (queue.length) {
let node = queue[queue.length - 1]; // Peek the stack
if (node !== null) {
queue.pop();
queue.push(node); // Node
queue.push(null);
depth++;
node.right && queue.push(node.right); // Right
node.left && queue.push(node.left); // Left
} else {
node = queue.pop();
queue.pop();
depth--;
}
res = res > depth ? res : depth;
}
return res;
}
var isBalanced = function (root) {
if (root === null) return true;
let queue = [root];
while (queue.length) {
let node = queue[queue.length - 1]; // Peek the stack
queue.pop();
if (Math.abs(getHeight(node.left) - getHeight(node.right)) > 1) {
return false;
}
node.right && queue.push(node.right);
node.left && queue.push(node.left);
}
return true;
};
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
# TypeScript:
Recursive Method
// Recursive Method
function isBalanced(root: TreeNode | null): boolean {
function getDepth(root: TreeNode | null): number {
if (root === null) return 0;
let leftDepth: number = getDepth(root.left);
if (leftDepth === -1) return -1;
let rightDepth: number = getDepth(root.right);
if (rightDepth === -1) return -1;
if (Math.abs(leftDepth - rightDepth) > 1) return -1;
return 1 + Math.max(leftDepth, rightDepth);
}
return getDepth(root) !== -1;
};
2
3
4
5
6
7
8
9
10
11
12
13
# C:
Recursive Method:
int getDepth(struct TreeNode* node) {
// If node does not exist, return 0
if(!node)
return 0;
// Get the depth of the right subtree
int rightDepth = getDepth(node->right);
// Get the depth of the left subtree
int leftDepth = getDepth(node->left);
// Return the larger value of left and right subtree depths + 1
return rightDepth > leftDepth ? rightDepth + 1 : leftDepth + 1;
}
bool isBalanced(struct TreeNode* root) {
// Recursive termination condition: If the passed node is NULL, return True
if(!root)
return 1;
// Calculate the depths of left and right subtrees
int leftDepth = getDepth(root->left);
int rightDepth = getDepth(root->right);
int diff;
// If the depth difference between left and right subtree > 1, return False
if((diff = leftDepth - rightDepth) > 1 || diff < -1)
return 0;
// Check if both left and right subtrees are balanced binary trees
return isBalanced(root->right) && isBalanced(root->left);
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
Iterative Method:
// Calculate node's depth
int getDepth(struct TreeNode* node) {
// Allocate space for stack
struct TreeNode** stack = (struct TreeNode**)malloc(sizeof(struct TreeNode*) * 10000);
int stackTop = 0;
// If the passed node exists, push it onto the stack. If not exist, the function returns 0 directly
if(node)
stack[stackTop++] = node;
int result = 0;
int depth = 0;
// Iterate while there are elements in the stack
while(stackTop) {
// Peek the top element of the stack
struct TreeNode* tempNode = stack[--stackTop];
// If the top element is not NULL, increase depth by 1
if(tempNode) {
depth++;
// Repush the top element, adding NULL to indicate this node has been traversed
stack[stackTop++] = tempNode;
stack[stackTop++] = NULL;
// If the top element has left and right children, push onto the stack
if(tempNode->left)
stack[stackTop++] = tempNode->left;
if(tempNode->right)
stack[stackTop++] = tempNode->right;
// Update result with the maximum depth
result = result > depth ? result : depth;
}
else {
// If NULL, it indicates current node has been traversed, decrease depth by 1
tempNode = stack[--stackTop];
depth--;
}
}
return result;
}
bool isBalanced(struct TreeNode* root){
// Allocate space for stack
struct TreeNode** stack = (struct TreeNode**)malloc(sizeof(struct TreeNode*) * 10000);
int stackTop = 0;
// If root node does not exist, return True
if(!root)
return 1;
// Push the root node onto the stack
stack[stackTop++] = root;
// Traverse while there are elements in the stack
while(stackTop) {
// Pop the top element of the stack
struct TreeNode* node = stack[--stackTop];
// Calculate depth of the left and right subtrees
int diff = getDepth(node->right) - getDepth(node->left);
// If the absolute value of depth difference > 1, return False
if(diff > 1 || diff < -1)
return 0;
// If the stack top node has left and right nodes, push them onto the stack
if(node->left)
stack[stackTop++] = node->left;
if(node->right)
stack[stackTop++] = node->right;
}
// If no return False ends here, return True
return 1;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
# Swift:
Recursive
func isBalanced(_ root: TreeNode?) -> Bool {
// -1 already means it is not a balanced binary tree
return getHeight(root) == -1 ? false : true
}
func getHeight(_ root: TreeNode?) -> Int {
guard let root = root else {
return 0
}
let leftHeight = getHeight(root.left)
if leftHeight == -1 {
return -1
}
let rightHeight = getHeight(root.right)
if rightHeight == -1 {
return -1
}
if abs(leftHeight - rightHeight) > 1 {
return -1
} else {
return 1 + max(leftHeight, rightHeight)
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# Rust:
Recursive Method
use std::cell::RefCell;
use std::rc::Rc;
impl Solution {
pub fn is_balanced(root: Option<Rc<RefCell<TreeNode>>>) -> bool {
Self::get_depth(root) != -1
}
pub fn get_depth(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
if root.is_none() {
return 0;
}
let right = Self::get_depth(root.as_ref().unwrap().borrow().left.clone());
let left = Self::get_depth(root.unwrap().borrow().right.clone());
if right == -1 {
return -1;
}
if left == -1 {
return -1;
}
if (right - left).abs() > 1 {
return -1;
}
1 + right.max(left)
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# C#
public bool IsBalanced(TreeNode root)
{
return GetHeight(root) == -1 ? false : true;
}
public int GetHeight(TreeNode root)
{
if (root == null) return 0;
int left = GetHeight(root.left);
if (left == -1) return -1;
int right = GetHeight(root.right);
if (right == -1) return -1;
int res;
if (Math.Abs(left - right) > 1)
{
res = -1;
}
else
{
res = 1 + Math.Max(left, right);
}
return res;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
